多目标短期梯级水电优化调度混合整数模型

葛晓琳,张粒子,王春丽

（华北电力大学电气与电子工程学院，北京 102206）

0 引言

根据节能发电调度的原则，在制定电力系统短期调度计划时，需要先由水库调度人员制定水电的发电计划和水库的调度计划，然后从负荷中扣除水电发电量部分作为火电应满足的负荷[1]。近些年来，随着水电资源的大规模开发，研究短期梯级水电优化调度的理论与方法，对于充分利用水能资源，贯彻落实“节能减排”政策均具有重要的理论意义和工程实用价值[2-4]。

短期梯级水电优化调度涉及的变量、约束较多，建模和求解规模较大，是一个难点问题。文献[5]综合考虑水头影响、不连续运行区间等约束建立了梯级水电系统短期调度的模型。文献[6]从减少水库系统弃水的角度出发，提出了最小弃水的梯级水库优化调度模型，提高了水资源利用率，也间接地实现了水库发电效益的最大化。文献[7]针对水力发电特性函数中库容、发电流量、机组出力三者之间的关系，利用先进的建模技术建立了这一三维函数的线性混合整数模型，使得短期水电优化调度的模型更为精确。文献[8]针对遗传算法容易出现“早熟”的现象，提出了一种基于实数编码技术的混沌遗传算法，并应用于求解水电短期经济运行问题。文献[9]考虑了水电站间的水力电力联系和水电价格建立了梯级水电系统短期发电计划通用模型。上述文献在短期梯级水电优化调度模型和方法方面取得了一定的进展，但这些文献都是基于广义的以水定电方法进行调度，从提高水能利用效率角度，将目标设定为调度期内库群的总发电量最大。经过优化的水力资源被优先安排发电，在电力系统中承担基荷，这种调度模型无法发挥水电的调峰性能。针对这一问题，文献[10]提出了调峰电量最大的调度方法，并在优化过程中采用了减少弃水的局部调整策略，但并未实现调峰能力和发电量效益的多目标协调优化。

基于上述背景，本文全面考虑水电机组调峰的灵活性及其经济效益，建立了多目标短期梯级优化调度混合整数规划模型。模型以扣除水电机组发电后总剩余负荷以及剩余负荷峰谷差最小化为多目标进行优化，实现水电系统综合效益的最大化。由于模型中包含的约束条件多、求解规模大，首先利用混合整数建模方法，将梯级水电机组发电的非线性约束线性化处理，然后基于模糊优化方法建立各个单目标的隶属函数将问题模糊化，定义满意度指标，将多目标问题转化为单目标规划问题。最后，利用目前先进的MILP求解软件包对所建模型进行求解。

1 数学模型

1.1 目标函数

在短期梯级水电优化调度中，一方面要充分利用水电这一清洁能源发电[11-12]，节约火电的燃料成本，降低污染物的排放；另一方面需要充分发挥水电良好的调峰性能，使得经水电削峰后的剩余负荷尽量平滑，减少火电机组出力的剧烈波动。因此，本文模型采用系统中扣除水电出力后的总剩余负荷量(简称余荷)和余荷峰谷差两个目标，余荷和余荷峰谷差如图1所示。

图1 系统剩余负荷曲线Fig. 1 Curve of surplus load

两个目标具体可以表示为

1）总余荷最小

2）余荷峰谷差最小

式中：T为计划周期内的时段总数；t为时段编号，t∈[1,T]；H为系统内的水电机组总数；h为水电机组编号； PD,t为t时段的系统负荷； ph,t为t时段机组h的出力； f1为总余荷； f2为余荷峰谷差。

1.2 约束条件

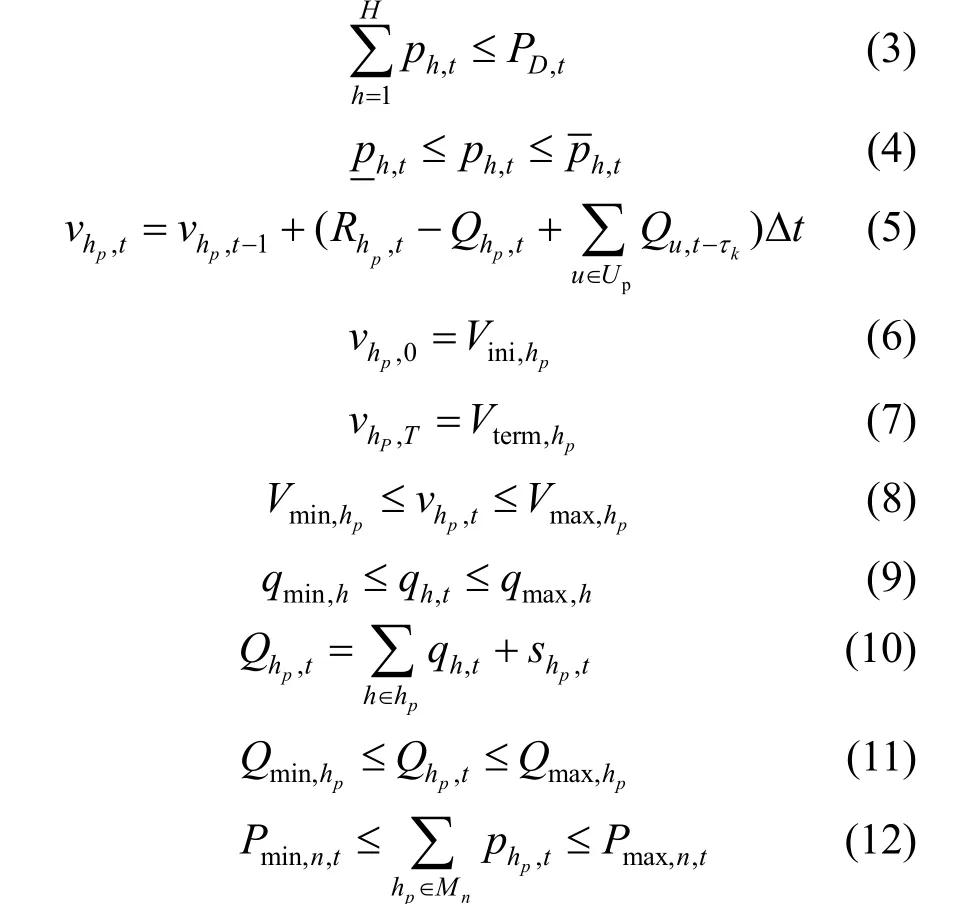
式中：ph,t、ph,t分别水电机组允许的出力上下限；vhp,t为t时段水电站 hp的库容； Rhp,t为t时段水电站 hp的自然来水流量；Qhp,t为t时段水电站 hp的下泄流量；UP代表其上游水电站集合；τ为上游电站u流至下游电站hp的水流延时；Δt为时段t内包含的秒数；Vini,hp、Vterm,hp分别为调度周期内始末的库容； Vmax,hp、 Vmin,hp分别为水电站 hp库容的上下限；qh,t为t时段机组h的发电流量； qmax,h、 qmin,h分别为机组发电流量的上下限； shp,t为t时段水电站 hp的弃水流量； Qmax,hp、Qmin,hp分别为下泄流量的上下限；Mn为第n个水电站集合；Pmax,m,t、Pmin,m,t为机组集合 Mn时段t的出力上下限。

2 模型的转换及求解

2.1 非线性约束的线性化

基于水电机组的特性，水电优化调度中不仅需要满足上述线性约束条件，还需要满足非线性的发电特性和出力限制曲线约束，这些复杂的约束需要进行转换才能利用混合整数规划算法[13-14]进行求解。受库容（水头）影响的非线性发电特性曲线的MILP模型具体如式(13)~式(21)所示。分段出力限制曲线的MILP模型具体如式(22)~式(25)所示。

式中：r为发电功率曲线中库容的分段编号，r∈[1,R]；qh,t,r为水电机组h在t时段r段库容下的发电流量。在r段库容下，发电功率可以表示为发电流量的线性函数，这里用 ahr、 bh,r分别表示第 h个水电机组r段库容下发电功率曲线的一次项和常数项；同时将发电流量分为两部分 q1,h,t,r， q2,h,t,r，其取值范围分别为[0,− bh,r/ah,r]，d1,h,t,r为 0、1变量，当 qh,t,r大于发电功率曲线与横轴交点处的横坐标时，取值为1，否则为0；Vhp,r为第r段库容；dh,t,r为0、1变量，当时取值为1，否则为0；qh,t为第h个水电机组在t时段的发电流量。s为出力限制曲线中库容的分段编号，s∈[1,S]；分别为第s段对应的出力上下限； Vhp,s为水电机组h所在水电站 hp的第s段库容； zh,hp,s,t为水电站 hp中第h个水电机组在第s段的状态变量，时取值为1，否则为0。

2.2 目标函数的线性化

利用文献[15]中的模糊隶属度函数对多目标函数进行线性化。对于 1.1节中的总余荷最小的目标函数，建立相应的隶属度函数，数学表达式为

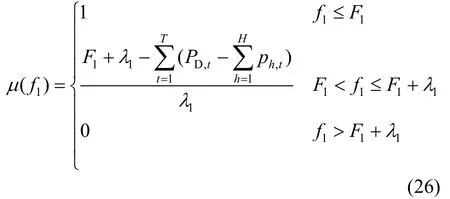
式中：F1为单独以总余荷最小优化得到的目标值；1λ为可接受的目标函数伸缩参数。

对于余荷峰谷差最小的目标，先建立目标函数的MILP模型，具体表达式为

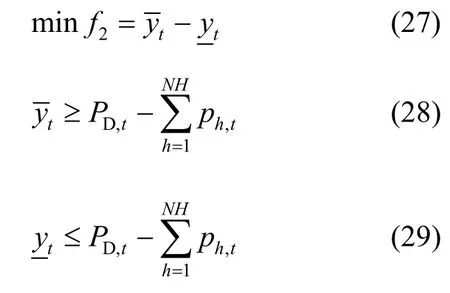
然后，建立目标函数余荷峰谷差最小的隶属度函数，表达式为

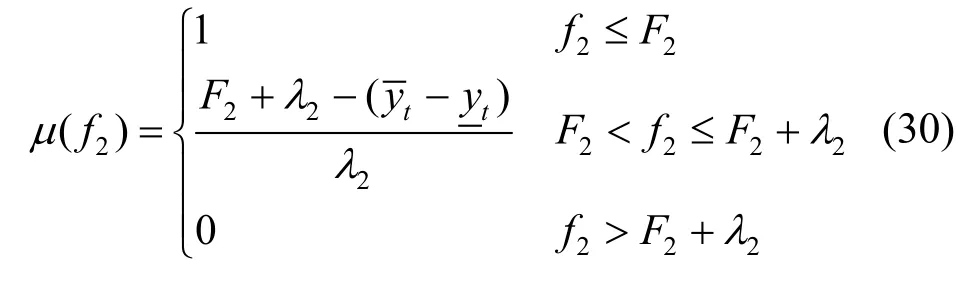
式中：F2为单独以余荷峰谷差最小优化得到的目标值；2λ为可接受的目标函数伸缩参数。

依据模糊优化原理，定义满意度指标δ，如下：

将它们分别代入式(26)和式(30) 中，即可将多目标模型就转化为满足约束条件的满意度δ最大化的MILP问题，其数学模型整理为

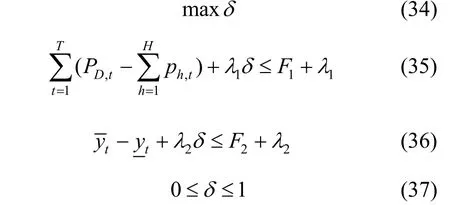
式中：δ为满足所有约束条件的满意度指标，单独以总余荷最小优化得目标值 F1和余荷峰谷差2F′，单独以余荷峰谷差最小优化得到目标值 F2和总余荷1F′；1λ、2λ为两目标的可接受伸缩参数，其取值范围为模糊优化中伸缩参数1λ、2λ的取值反映了调度决策的意愿，例如当伸缩参数1λ取值越小时，其相应的目标在最终决策中所占的权重越大。

此外，上述目标函数还需满足式(3)~式(25)的约束条件。所建模型的求解流程如图2所示。

图2 计算流程图Fig. 2 Flow chart of calculation

3 算例分析

某地区的水电系统包含了 13个梯级分布的水库和44台水电机组，调度周期为24小时，各时段的系统负荷参数见表1。测试的环境为CPU P4 2.4 GHz、内存1 GB，通过GAMS建模平台，调用先进的CPLEX11.0优化软件包进行求解。

结合本算例，通过计算伸缩参数1λ、2λ的取值范围分别是[0，4693.43]、[0，527.83]。为了分析1λ、2λ对调度结果的影响，在1λ、2λ取值范围内等间距选取了10种情况，如表2所示。针对这10种情况分别进行了求解，得到的优化解如图3所示。

表1 典型日负荷Table 1 Typical daily load

从图3中可以看出，伸缩参数1λ、2λ的取值对最终决策有一定的影响，当伸缩参数取值越小时，其相对应的目标越接近单目标优化的最优值。因此，在枯水期时，水电需要多承担调峰作用，这时可以将峰谷差最小的伸缩参数2λ取值较小，而余荷总量最小的伸缩参数1λ取值较大；同样在丰水期为了减少弃水，充分利用水电资源，则可将1λ取值较小，2λ取值较大。总之，对于实际电力系统调度，可根据调度要求对伸缩参数进行选取，并选择一种方案作为最终的调度结果。

表2 伸缩参数的取值Table 2 The value of stretching parameter

图3 伸缩参数对调度结果的影响Fig. 3 The influence of stretching parameters on the dispatching

为了比较多目标和单目标的调度决策结果，选取3种情况进行分析，1）单独以总余荷最小进行优化；2）单独以余荷峰谷差最小进行优化；3）进行多目标优化，1λ、2λ分别取值为2346.71 MW、316.70 MW(情况5)。3种情况的优化结果如图4所示，从图中可以看出，单独以总余荷最小进行优化，系统负荷扣除水电机组发电后的余荷曲线仍然具有较大的峰谷差，火电机组势必要完成调峰任务，将会增加调度的难度和相应的燃料费用。但若仅以余荷峰谷差最小进行优化，水电资源难以得到充分的利用，并产生大量弃水。本文综合考虑总余荷量最小和余荷峰谷差最小两个目标，经过优化使得各个目标都尽可能处于较优状态，从而得到更具可行性的梯级水电调度方案。

图4 优化后的负荷曲线Fig. 4 Optimized load curve

4 结论

本文在满足梯级水电站水力电力联系、非线性发电曲线、分段出力限制等约束条件下，综合考虑水电发电效率和调峰性能，建立了梯级水库群的多目标短期优化调度模型，并基于模糊隶属度函数和混合整数建模方法，将模型转换为单目标混合整数线性规划问题进行求解。计算结果表明该调度模型既能够充分利用水电资源，又可以发挥水电机组的调峰特性，从而得到更加可行的调度方案。同时，调度员可以根据不同的调度要求对伸缩参数进行调整，使得调度方案能够满足不同来水特性下的电网运行要求。

[1] 陈雪青, 陈刚, 张炜, 等. 电力系统长、中、短期能源调度管理系统的研究[J]. 中国电机工程学报, 1994,14(6): 41-48.CHEN Xue-qing, CHEN Gang, ZHANG Wei, et al. Long,medium and short-term energy management systems of large power systems[J]. Proceedings of the CSEE, 1994,14(6): 41-48.

[2] 纪昌明, 刘方, 喻杉, 等. 基于鲶鱼效应粒子群算法的梯级水库群优化调度[J]. 电力系统保护与控制, 2011,39(19): 63-68.JI Chang-ming, LIU Fang, YU Shan, et al. The optimal operation of cascade reservoirs based on catfish effect particle swarm optimization algorithm[J]. Power System Protection and Control, 2011, 39(19): 63-68.

[3] WANG Jin-wen. Short-term generation scheduling model of Fujian hydro system[J]. Energy Conversion and Management, 2009, 50(4): 1085-1094.

[4] 谢维, 纪昌明, 杨子俊, 等. 水电站短期发电调度规则制定[J]. 电力系统保护与控制, 2011, 39(21): 98-103.XIE Wei, JI Chang-ming, YANG Zi-jun, et al. The short-term power generation scheduling rules for hydropower station[J]. Power System Protection and Control, 2011, 39(21): 98-103.

[5] 贾江涛, 管晓宏, 翟桥柱. 考虑水头影响的梯级水电站群短期优化调度[J]. 电力系统自动化, 2009, 33(13):13-16.JIA Jiang-tao, GUAN Xiao-hong, ZHAI Qiao-zhu.Short-term optimal scheduling of head-dependent cascaded hydropower stations[J]. Automation of Electric Power Systems, 2009, 33(13): 13-16.

[6] 原文林, 黄强, 王义民, 等. 最小弃水模型在梯级水库优化调度中的应用[J]. 水力发电学报, 2008, 27(3):16-21.YUAN Wen-lin, HUANG Qiang, WANG Yi-min, et al.Application of minimal abandoned water model in optimal operation of cascade reservoirs[J]. Journal of Hydroelectric Engineering, 2008, 27(3): 16-21.

[7] Borghetti A, Dambrosio C, Lodi A, et al. An MILP approach for short-term hydro scheduling and unit commitment with head-dependent reservoir[J]. IEEE Trans on Power Systems, 2008, 23(3): 1115-1124.

[8] 袁晓辉, 王乘, 张勇传, 等. 水电系统短期经济运行的新方法[J]. 水力发电学报, 2006, 25(4): 1-5.YUAN Xiao-hui, WANG Cheng, ZHANG Yong-chuan,et al. A new algorithm for short-term economic operation of hydropower system[J]. Journal of Hydroelectric Engineering, 2006, 25(4): 1-5.

[9] 曾勇红, 姜铁兵, 张勇传. 基于线性规划的梯级水电系统短期发电计划[J]. 水电自动化与大坝监测, 2004,28(4): 59-62.ZENG Yong-hong, JIANG Tie-bing, ZHANG Yong-huan.Linear programming-based short-term generation scheduling for cascade hydropower systems[J]. Hydro Power Automation and Dam Monitoring, 2004, 28(4):59-62.

[10] 王金文, 范习辉, 张勇传, 等. 大规模水电系统短期调峰电量最大模型及其求解[J]. 电力系统自动化, 2003,27(15): 29-34.WANG Jin-wen, FAN Xi-hui, ZHANG Yong-chuan,et al. Short-term generation scheduling for the peak-energy maximization of large-scale hydropower systems[J]. Automation of Electric Power Systems, 2003,27(15): 29-34.

[11] Pérez-Díaz J I, Wilhelmi J R. Short-term operation scheduling of a hydropower plant in the day-ahead electricity market[J]. Electric Power Systems Research,2010, 80(12): 1535-1542.

[12] 韩冰, 张粒子, 舒隽. 梯级水电站代理竞价模型及均衡求解[J]. 中国电机工程学报, 2008, 28(22): 94-99.HAN Bing, ZHANG Li-zi, SHU Jun. Bidding model of cascaded hydropower stations and equilibrium solving under agency mechanism[J]. Proceedings of the CSEE,2008, 28(22): 94-99.

[13] 苏济归, 舒隽, 谢国辉, 等. 大规模机组组合问题计及网络约束的线性化求解方法[J]. 电力系统保护与控制,2010, 38(18): 135-139.SU Ji-gui, SHU Jun, XIE Guo-hui, et al. Linearization method of large scale unit commitment problem with network constraints[J]. Power System Protection and Control, 2010, 38(18): 135-139.

[14] Chang G W, Aganagic M, Waight J G, et al. Experiences with mixed integer linear programming based approaches on short-term hydro scheduling[J]. IEEE Trans on Power Systems, 2001, 16(6): 743-749.

[15] 温丽丽, 刘俊勇. 混合系统中、长期节能调度发电计划的蒙特卡罗模拟[J]. 电力系统保护与控制, 2008,36(24): 24-29.WEN Li-li, LIU Jun-yong. Monte Carlo simulation of medium and long-term generation plan in hybrid power system based on environmental/economic dispatch[J].Power System Protection and Control, 2008, 36(24):24-29.