Annulus and Disk Complex Is Contractible and Quasi-convex
GUO QI-LONG,QIU RUI-FENG,ZOU YAN-QINGAND ZHANG FA-ZE
(1.School of Mathematics Sciences,Dalian University of Technology,Dalian,Liaoning,116023) (2.Department of Mathematics,East China Normal University,Shanghai,200062)
Communicated by Lei Feng-chun
Annulus and Disk Complex Is Contractible and Quasi-convex
GUO QI-LONG1,QIU RUI-FENG2,ZOU YAN-QING1AND ZHANG FA-ZE1
(1.School of Mathematics Sciences,Dalian University of Technology,Dalian,Liaoning,116023) (2.Department of Mathematics,East China Normal University,Shanghai,200062)
Communicated by Lei Feng-chun
The annulus and disk complex is defined and researched.Especially,we prove that this complex is contractible and quasi-convex in the curve complex.
annulus and disk complex,contractible,quasi-convex
1 Introduction
Let S be a closed orientable surface with genus at least 2.Harvey[1]defined the curve complex of S as follows.The curve complex of S is the complex whose vertices are the isotopy classes of essential simple closed curves on S,and k+1 vertices in the curve complex span a k-simplex if they are represented by pairwise disjoint curves.We denote the curve complex of S by C(S).Harer[2]proved that C(S)is homotopy equivalent to a bouquet of spheres of dimension-χ(S).
If S is a boundary component of an irreducible 3-manifold M,then we can define the disk complex Δ(M,S)as in[3].A vertex of Δ(M,S)is an isotopy class of an essential curve in S which bounds a disk in M.As in the Definition of C(S),k+1 vertices in Δ(M,S) span a k-simplex if they are represented by pairwise disjoint curves.It is easy to see that Δ(M,S)is a subcomplex of C(S).McCullough[3]researched this complex and proved that it is contractible.
In Section 2,we define a new complex associated to a compression body as a generalization of both curve complex and disk complex of a handlebody.For a compression body C, we denote this new complex by AD(C)and call it annulus and disk complex.By using the techniques in[3],we prove the following theorem:
Theorem 1.1The annulus and disk complex AD(C)is contractible.
A metric space(X,d)is geodesic,if for any pair of points there is a path connecting them which is a geodesic;and a subset Y of(X,d)is K-quasi-convex if for any pair of points in Y,any geodesic in X connecting them lies in a K-neighborhood of Y.A result in[4] implies that Δ(M,S)is quasi-convex in C(S).By the aid of their results,we prove
Theorem 1.2AD(C)is K-quasi-convex in C(S),where K depends only on the genus of S.
2 Preliminaries
Definition 2.1A compression body C is a 3-manifold obtained from an orientable connected closed surface Σ by attaching 2-handles to Σ×{1}⊂Σ×[0,1]and 3-balls to 2-sphere boundaries thereby created.We write

When C=Σ×[0,1],we say that C is a trivial compression body.When∂-C=Ø,we say that C is a handlebody.
Remark 2.1If F is an essential annulus properly embeded in a compression body C,then this annulus must have one boundary component in∂+C as the other boundary component in∂-C.Furthermore,if F1and F2are two essential annuli such that F1∩∂+C is isotopic to F2∩∂+C in∂+C,then F1is isotopic to F2in C.
Essential annuli play an important role in the following definition.
Definition 2.2For a compression body C,the annulus and disk complex AD(C)is defined as follows:A vertex of AD(C)is an isotopy class of an essential curve on∂+C which bounds an essential disk in C or cobounds an essential annulus in C with another curve in
Remark 2.2If C is a trivial compression body,then AD(C)is nothing but the curve complex C(∂+C).If C is a handlebody,then AD(C)is the disk complex Δ(C,∂+C).
Then we define another complex associated to a compression body C without concerning∂+C.
Definition 2.3For a compression body C,the complexis defined as follows:A vertex ofis an isotopy class of an essential disk in C or an essential annulus in C. k+1 vertices[F0],···,[Fk]determine an k-simplex if and only if we can isotopy F0,···,Fkso that they are mutually disjoint.
Lemma 2.1The map]can be extended to be an isomorphism from
As in[5],we give the Definition of δ-hyperbolic spaces.
Definition 2.4A geodesic space X is said to be δ-hyperbolic with constant δ≥0,if for every geodesic triangle xyz in X,one sideis contained in the closed δ-neighborhood of the union of the other two sides
Lemma 2.2[6]C(S)is δ-hyperbolic for some constant δ>0,where δ depends only on the genus of S.
Lemma 2.3[4]Suppose that M is a compact,orientable 3-manifold M with boundary component S.Then Δ(M,S)is a K-quasi-convex subset of C(S),where K depends only on the genus of S. and
3 Proof of Theorem 1.1
The proof of Theorem 1.1 is similar to the proof of Theorem 5.3 in[3].
It is easy to see that we only need to prove that any map from any sphere to X is null-homotopic.Suppose that the map f:Sq→X is given.
Define Ω:={(K,g):K is a triangulation of Sq,g:Sq→X is homotopic to f,and g:K→X is simplicial}.
Next,we define a complexity function P on Ω as follows.
Let E be an essential disk of C.Then a=[E]is a vertex of X.
For any pair(K,g)∈Ω,define Pi(K,g)to be the number of vertices v of K such that g(v)·a=i.The complexity P(K,g)is defined by(···,P3(K,g),P2(K,g),P1(K,g)),and the complexities are ordered lexicographically.
Suppose that(K,g)has the minimal complexity among all elements in Ω.
If Pi(K,g)=0 for each i,then each vertex of K is carried intoby g.Since g is simplicial and,by Lemmas 2.2 and 2.3,g is null-homotopic.Hence f is also null-homotopic.
Therefore,suppose that Pi(K,g)=0 for all i>n and Pn(K,g)>0 for some n>0. Choose a vertex v0∈K such that g(v0)·a=n.Let v1,v2,···,vkbe the vertices in Kadjacent to v0,and we can choose representatives Fifor each g(vi)so that Fiintersects Fjminimally∩for eachand each Fiintersects E minimally(i.e.,=Ø for each i/=0.
中等厚度靶(中厚靶)通常是指靶板厚度与撞击形成的坑深大致相等。如上所述,当厚靶的厚度远大于坑的深度时,靶板的后表面,即自由面对成坑几何尺寸没有影响。但是实际上,靶都是有限厚的,无限厚靶属于一种极限情况。弹丸超高速侵彻中厚靶的瞬态阶段及主要侵彻阶段与弹丸超高速侵彻无限厚靶的情况完全相同,只有当靶板后表面反射的稀疏波到达侵彻坑底部之后,才会表现出与无限厚靶板侵彻过程的差异,即向前的应力波和靶板后表面反射的稀疏波相遇产生拉伸应力,当拉伸应力大于靶板的拉伸断裂强度时,靶板后表面发生层裂。图5为球形弹丸超高速侵彻中等厚度靶导致靶板后表面产生层裂的现象。
Since n>0,F0is not disjoint from E.Consider an arc α of their intersection which is outermost in E.There is a disc B⊂E such that∂B⊂α∪∂E and int(B)∩F0=Ø.
There are two possibilities.
Since F0intersects E minimally,by surgery on F0along B we get two essential surfaces, one of which is an essential disk(denoted by)and the another is a spanning annulus or an essential disk,and we can see that∩.Since(F0∪B)∩Fi=Ø for each i/=0, and∩we get that if[Fi1],···,[Fim]and[F0]are contained in a common simplex of X for some i1,···,im,then Fi1,···,Fim,F0and F′0are mutually disjoint.Hence[Fi1], ···,[Fim],[F0]and[F′0]are also contained in a common simplex of X.
Claim 3.1is homotopic to g.
Proof.Since the difference part of the two maps is only on the carrier simplex of{v0,···,vk} in K,we canfind a homotopy gtsuch that
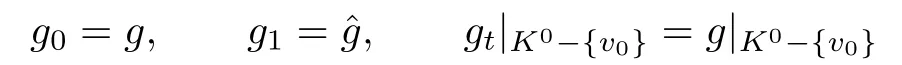
and gt(v0)slides on the 1-simplex〉when t increases from 0 to 1.Actually,if Δ is a simplex of K which does not contain v0,then

and if Δ is a simplex of K containing v0,then gt|Δis defined by linear expansion,and this can be done since g|t(v0),···,g|t(vk)are contained in a common simplex of X.
Let β be an arc of intersection of some Fiand B which is outermost in B and contains no arcs of any Fjwhich is disjoint from Fi(note that β may still intersect an arc of some B∩Fjfor some j/=i).Then by surgery Fialong B,we get an essential diskas above, and can see that.Hence ifand[F0](or[Fi]) are contained in a common simplex of X for some i1,···,im,then[Fi1],···,[Fim],[F0](or [Fi])andare also contained in a common simplex of X.
Claim 3.2g′is homotopic to g.
Proof.Since F0,Fi,are mutually disjoint,and[F0],[Fi],are contained in a simplex of X,which also contains,there is a segment connectingand.For each t∈[0,1],we define gt(x)=x if x/=viandto be a point in the segmentsuch that

Then we can extend each gtto the whole Sqas follows.If Δ is a simplex which does not contains,then define gt|Δ=g0|Δ.If Δ contains,then gt|Δis defined by linear expansion in Δ.It is easy to see that
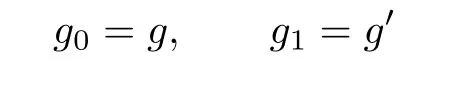
and gtis a homotopy between g and g′.
Now P(K1,g1)>P(K,g),because we have added the new vertex v′mapping toBut·[E]<[Fk]·[E]<n since n is maximal,and hence

Repeating finitely many times,we obtain a subdivision K2of K and a simplicial map g2:K2→X homotopic to g such that

and int(B)is disjoint from the representative surfaces for the vertices{g2(v1),···,g2(vk)}. Now,by surgery F0along B as in Case 1,we can find a simplicial map g3:K2→X which is homotopic to g2and satisfies that

and

Hence P(K2,g3)<P(K,g),which contradicts the choice of(K,g).
4 Proof of Theorem 1.2
For any pair of two vertices[F1],[F2]in AD(C),let γ be any geodesic joining them.Let K be the constant in Lemma 2.5 in the case that M=C and S=∂+C.
There are three cases about F1and F2.
Case 1.Both are disks.
In this case,Lemma 2.5 implies Theorem 1.2.
Case 2.F1is a disk,while F2is an annulus.
Choose an essential disk D of C such that D∩F2=Ø.Let β be the 1-simplex joining [D]and[F2],and α be a geodesic joining[D]and[F1].By the hyperbolicity of C(S),α is in the δ-neighborhood of β∪γ.By Lemma 2.6,γ is in the K-neighborhood of Δ(M,S).Since Δ(M,S)⊂AD(C)and β is in the 1-neighborhood of AD(C),α is in the(K+δ+1)-neighborhood of AD(C).
Case 3.Both F1and F2are annuli.
The proof of this case is similar to that in Case 2,and we can choose the constant to be K+2β+1.
[1]Harvey W J.Boundary Structure of the Modular Group.In:Kra I,Maskit B.Riemann Surfaces and Related Topics:Proceedings of the 1978 Stony Brook Conference.New Jersey:Princeton Univ.Press,1981:245–251.
[2]Harer J.The virtual cohomological dimension of the mapping class group of an orientable surface.Invent.Math.,1986,84:157–176.
[3]McCullough D.Virtually geometrically finite mapping class groups of 3-manifolds.J.differential Geom.,1991,33:1–65.
[4]Masur H,Minsky Y.Quasiconvexity in the Curve Complex.in:Abikof fW.In the tradition of Ahlfors and Bers III.Amer.Math.Soc.RI:Providence,2004:309–320.
[5]Bridson M R,Haef l iger A.Metric Spaces of Non-positive Curvature.Grundlehrender Mathematischen Wissenschaften,319.Berlin:Springer,1999.
[6]Masur H,Minsky Y.Geometry of the complex of curves I:Hyperbolicity.Invent.Math.,1999, 138:103–149.
57M99
A
1674-5647(2013)04-0377-06
Received date:April 6,2012.
The NSF(10901029)of China.
E-mail address:guoqilong1984@hotmail.com(Guo Q L).
 Communications in Mathematical Research2013年4期
Communications in Mathematical Research2013年4期
- Communications in Mathematical Research的其它文章
- Stability of Cubic Functional Equation in Three Variables
- A New Kind of Iteration Method for Finding Approximate Periodic Solutions to Ordinary Differential Equations
- The First Initial Boundary Value Problem for Parabolic Hessian Equations on Riemannian Manifolds
- A Gorni-Zampieri Pair of a Homogeneous Polynomial Map
- Principal Quasi-Baerness of Rings of Skew Generalized Power Series
- On Results the Growth of Meromorphic Solutions of Algebraic differential Equations
