2012江苏高考物理14题要点突破
——不计质量的力学模型
潘霞娟
(江苏省黄埭中学 江苏 苏州 215143)
审题能力与构建能力是物理高考中考生所必须具备的能力,它要求考生在高度紧张的环境中能静下心来审题,找到题目所设定的特殊已知条件,从而建立适当的物理模型,找到解决问题的方法.
下面以2012年江苏高考物理卷第14题为例分析如何寻找解决问题的突破口并建立模型.
【题目】某缓冲装置的理想模型如图1所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f.轻杆向右移动不超过l时,装置可安全工作.一质量为m的小车若以速度v0撞击弹簧,将导致轻杆向右移动.轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.
(1)若弹簧的劲度系数为κ,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v的关系.
考生由于习惯思维的影响,分析轻杆的运动情况时,往往会认为轻杆向右移动的过程中,弹簧先压缩再恢复形变,轻杆在弹簧弹力的作用下,先做加速度增加的加速运动,至弹簧压缩量最大,再做加速度减小的加速运动至形变量为x,最后,轻杆做减速运动至速度为零.对轻杆的运动做了较为细致的动态分析,花费了大量考场时间,题目仍然无法解决.
在这里,考生出现思维障碍的关键是“轻杆”两字.那么什么是“轻杆”,轻杆有何特殊之处呢?实际上,这是本题考查学生能力的关键之处.
解析:(1)不计轻杆质量.
结论1:由F合=ma得轻杆受力平衡.但是a不一定为零.
对轻杆分析:轻杆运动过程中,弹簧弹力始终等于滑动摩擦力,即弹簧的压缩量保持不变;
对小车分析:因弹簧弹力不变,小车在轻杆动起来后,做匀减速运动.
再对轻杆分析:弹簧的压缩量不变,则轻杆也随小车一起运动,且运动情况相同.
结论2:轻杆启动所用时间为零,速度突变至与小车速度相同.
结论3:轻杆有速度变化,但没有动能变化.
(2)利用能量守恒可知,小车从撞击到停止的过程为
小车动能的减少量=弹簧弹性势能+摩擦生热的内能

由式(1)、(2)得
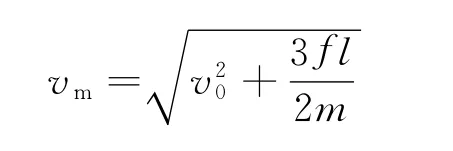
(3)分两种情况讨论,若轻杆运动了,则小车与轻杆匀减速运动至速度为零后,轻杆静止,小车在弹簧弹力作用下反弹的过程弹性势能等于小车获得的动能

由式(1)、(3)得

若轻杆一开始就没有运动,则小车以原速率反弹.所以

那么,对于不计质量的物体的研究,考生在以往的练习中是否有所接触呢?
【例1】2011年江苏高考物理卷第9题中关键词“轻质绸带”.绸带质量为零,受力平衡,两侧物体受到的摩擦力必然相等.
【例2】探究加速度与力、质量的关系实验中如图2所示,实验误差分析时,我们会分析到为什么细线的张力不等于物体B的重力.同时,也会出现这样一个问题即细线对物体A和B的拉力为什么相等?为什么考生接触到的题目中,同一根绳子中的张力处处相等?在这里,都涉及到同一个模型,不计质量的“轻质细线”.
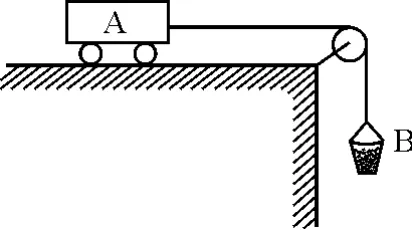
图2
【例3】如图3所示,甲和乙两个小球固定在一根轻杆的两端,此杆可绕穿过其中心的水平轴O无摩擦转动.现使轻杆从水平状态无初速度释放,发现杆绕O沿顺时针方向转动,则杆从释放起转动90°的过程中
A.乙球的重力势能减少,动能增加
B.甲球的重力势能增加,动能减少
C.甲球的重力势能和动能都增加了
D.甲球和乙球的总机械能是守恒的
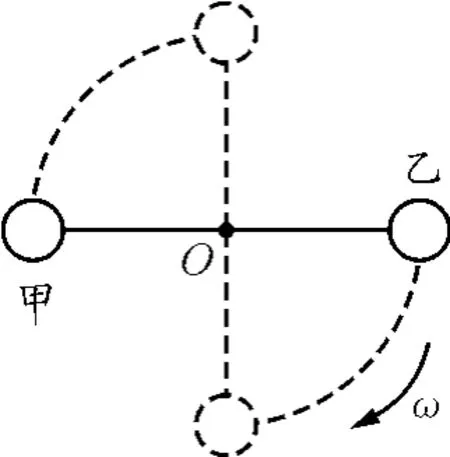
图3
本题中同样涉及到不计质量的物体“轻杆”.由于杆子的质量不计,在运动过程中,杆子也就没有动能与势能的变化.所以,我们认为甲球和乙球组成的系统机械能守恒.若要考虑杆子质量,则甲球、乙球和杆子三物体组成的系统机械能守恒,能量转化复杂些,不属于高中物理考生研究的范畴.

