注重过程和方法 落实课程目标——一道2013年连云港数学中考试题的教学启发

江苏省金湖县实验中学 高 峰 （邮编：211600）

数学在培养人的思维能力和创新能力上具有不可替代的作用.这种育人价值具体体现在：学习用数学的观点审视客观世界，用数学思想方法自然合理地思考问题，我们称之为数学的思维方式.具体的知识容易遗忘，但是这些认知能力的形成，影响着人的一生，从这种意义上说，相比具体的知识和技能等基础性目标，学会用数学的思维方式自然地思考问题具有更高的教育价值，这也是数学教学应该追求的高阶目标.那么如何让学生学会数学的思维方式呢？中考对教师教学方式和学生学习方式具有引领作用.研究中考题有利于教师的教学观念的更新，对教学实践具有良好的借鉴和导向作用.下面就通过一道中考试题来管窥一下这个问题.

1 试题呈现

题目 （2013江苏连云港中考卷）小明在一次数学兴趣小组活动中，对一个数学问题作如下探究：

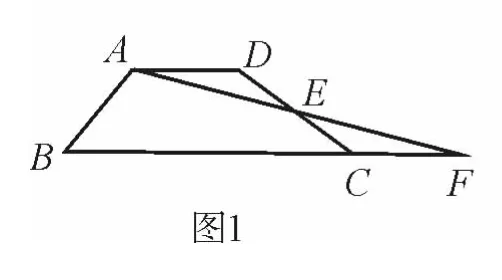
问题情景 如图1，四边形ABCD中，AD∥BC，点E为DC边的中点，连结AE并延长交BC的延长线于点F.求证：S四边形ABCD＝S△ABF.（S表示面积）

问题迁移 如图2，在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN，分别交射线OA、OB于点M、N.小明将直线MN绕点P旋转的过程中发现，△MON的面积存在最小值.请问当直线MN在什么位置时，△MON的面积最小，并说明理由.

实际应用 如图3，若在道路OA、OB之间有一村庄Q发生疫情，防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线，建立一个面积最小的三角形隔离区△MON.若测得∠AOB＝60°，∠POB＝30°，OP＝4km，试求 △MON的面积.（结果精确到0.1km2）（参考数据：sin66°≈0.91，tan66°≈2.25，≈1.73）.

2 试题分析

1 试题结构

“问题情境”涉及的图形是苏科版八、九年级教材中研究梯形中位线的一个“基本图形”，即如何将梯形转化为三角形.这是一个教材中被挖掘最多的素材，其中研究与面积有关的问题也是常见的问题.“问题迁移”与“问题情境”相比，表象发生了很大的变化，似乎两者没有什么联系，但是本质不变，大胆类比、猜想，不难发现结论，但要说明道理，就要对新的问题情景认真分析、触类旁通、灵活转化，才能找到解题的切入点，考查了学生转换和归纳推理的能力，有一定的难度.“实际应用”实际就是以“问题情境”的结论为载体，直接应用，思维并不复杂.“拓展延伸”实际是要求应用从“问题情境”到“问题迁移”获得经验并进行应用，这需要去充分消化、吸收这些经验去寻找解决问题的突破口，考查了学生学习和用新知识的能力.

2 思路分析

“问题情境”是一个熟悉的问题，通过对它的解决，一是激发化归经验，二是要自觉地把它作为一个“模型”.

“问题迁移”可先从特殊情形入手，这时最易想到的应该是OP与MN垂直和P是MN的中点，但思考证明是难点，即证明其它的情形得到面积都比它小，是一个不常见的证明方法，这里涉及合情推理和演绎推理.在证明时需要思考如何将“问题迁移”的图形转化为“问题情境”的图形（如图5），利用“问题情境”的模型解决问题，其中的关键是挖掘一个隐含条件——P是MN的中点.

“实际应用”的图形与“问题迁移”图形一致，直接类比应用，但是在求面积时要求高和底，需要通过作垂线，将一般三角形转化为直角三角形和相似三角形等来解决问题（如图6），其中融合了三角形中位线、三角函数、相似三角形等知识.

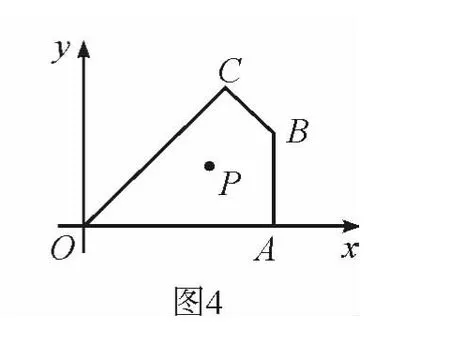
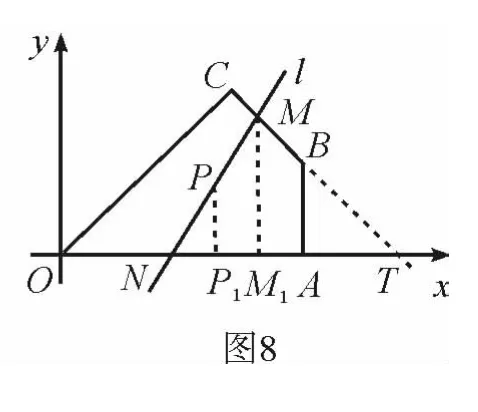
“拓展延伸”要学会自觉地运用前面的解题经验，首先通过操作可以发现，直线l的位置有两种.这时涉及的两个图形都是四边形，而前面“问题情境”的图形是四边形，要求的面积是最大值，而“问题迁移”的涉及是三角形的面积是最小值，这时只需要把四边形转化为三角形，“最大问题”转化为“最小问题”.由于原四边形面积一定，所以要其中一个最大，只需另一个最小即可（如图7和图8）.

3 教学启示

本题以学生熟悉的问题为背景，以操作探究的形式将问题递进，进而达成知识的应用，实现知识和信息的迁移和发展，凸现了对学习自主探究、归纳推理和应用能力的考查.问题解决的过程中，能有效地促进思维方式的形成.

3.1 注重“思维套路”

数学教育在学校育人的过程中具有独特的作用，其主要体现在开发学生的智力，锻炼学生的逻辑思维，使学生学会认识问题和解决问题的基本方法，并在这个过程中提高推理能力，培育理性精神和创造力.而要实现这个目标的基本途径就是使学生在认识数学的基本方法的同时，学会数学地思考和解决问题.而要达到这一点，必须把握数学地认识和解决问题的“基本套路”.本题充分体现了数学地认识和解决几何问题的一个“基本套路”，即思维方式.

追寻本题的命题思路：“问题情境”给出了一个“基本图形”并要求探究它的性质，这与平时探究三角形、四边形等“基本图形”的性质是一致的.“问题迁移”只需在新问题的图形中去寻找或构造出“问题情境”的“基本图形”，然后利用这个“基本图形”的性质即可解决问题，这与平时运用三角形、四边形等图形解决问题的思路一致.“实际应用”和“拓展延伸”只需利用在解决“问题迁移”中所获得的经验来解决问题，即构造出“问题迁移”的“基本图形”即可解决问题.

解决几何问题的一个“基本套路”就是：首先要认真分析条件，而分析条件就是将条件与相关“基本图形”结合起来，利用这个“基本图形”的性质，获得相应的结论.有时图形中不一定有与条件匹配的“基本图形”，这时还需联想相关知识作辅助线构造出相关的“基本图形”，再利用这个“基本图形”的性质，获得相应的结论，从而达到解决问题的目的.本题综合考查学生对“数学整体认识及研究数学问题的方法”和“形成解决问题的一些基本策略”的能力，这是“数学”的方法，体现继续学习的潜能.

这个“基本套路”还体现了提炼模型，应用模型的过程，这个过程有利于学会迁移知识和方法，形成应用意识.数学模型实质是一个数学问题在剔除无关信息后的本质特征，识别、提炼基本模型，以模解题，能有效地沟通相关问题情境，有效地促进解题过程中知识、方法的正向迁移，打破思维定势，化陌生为熟悉，化非常规为常规，有助于体验数学基本经验在解决实际问题中的价值和作用，强化应用意识.

3.2 把握问题设计

《义务教育数学课程标准（2011版）》提出“四基”，其中“基本活动经验”作为一项新目标，学生从事数学与综合实践活动的过程也渐趋走进命题者视野，颇受命题者的青睐.往往通过设计一个“做数学”和“玩数学”的活动，让学生通过观察、操作、实验、归纳、类比等系列活动获得数学猜想，寻求解释猜想的合理性并运用提炼的结论解决现实问题，它是学生形成数学思维方式的有效过程.

基于此，我们在设计问题时，要多角度、全方位挖掘已选素材的潜力，实现各个问题的承载功能，因此问题的创设要具有得体性和关联性，便于学生在解决过程中，汲取多层面的外在显性知识（如学会某种运算、能画出某种图形、获得某种数量关系、获得某种数学思想……）和潜滋暗长的多元生命感悟以及起着统领全局作用的内隐知识（数学思想）.同时得体性和关联性还指问题设置要由浅入深，呈梯度推进，便于学生思维够得着、可实验，前面的问题为后继思维提供必备的基础，待猜想问题一旦得到验证，即可解释前面问题操作的合理性.

本题的第（1）问源自课本，解决方法立足通法——三角形全等，对后继问题的解决起着心理、知识和方法的铺垫作用.第（2）问前面部分进行合理猜想获取结论，后面说理部分，命题者暗示了借助第（1）问的结论引申探究，提醒关注知识的生长点和延伸点，处理好局部和整体的关系，弄清楚其中所蕴涵的数学本质，为第（2）、（3）的有效解决提供知识储备.本题陈述简明，图形简约，构造巧妙，问题前后设计逐层递进，思维引导拾级而上.

3.3 注意体现过程

数学课程目标包括结果目标和过程目标，而所有这些目标的达成都源于问题，而问题的解决则在于对“过程”的思考.就价值引领而言，过程比结果更重要，因为结果仅是产物，而过程却是数学创造的源泉.本题的过程性主要体现在对△MON的面积何时最小的获得和应用过程，其中伴随着问题解决的全过程（发现和提出问题、分析和解决问题）.事实上，辅助线的添加过程就是问题解决过程，由于学生添加辅助线的能力较弱，因此不能准确切入，造成思维的断层和问题的搁浅.

“问题迁移”环节，在直观几何的帮助下，以直线MN旋转到普通位置为中介，过点M做射线OB的平行线即可获得△MON的面积最小的直观理解和理性解释.“实际应用”环节，过点M、P分别作射线OB的垂线，构造直角三角形，在“问题迁移”结论的帮助下，借助直角三角形获取待求结论.“拓展延伸”环节，在分类思想的统领下，借助已经积累的实践经验，在比较法的参与下，间接获取截得四边形面积的最大值为10.

3.4 问题要关注核心

本题并非是解题方法和技巧的机械运用，而是巧妙考查了学生的化归思想、建模思想、分类思想、方程与函数思想等，强化了对数学理性思维能力要求，展现了数学的学科价值和人文价值.

“基本思想方法、基本活动经验”是《义务教育数学课程标准（2011版）》新增的课程目标，将原来的“双基”发展为“四基”.本题的考查都是从数学思想方法的视角进行考查，要使得问题得到解决，可归结于学生的基本经验.在解决问题的过程中也充分体现了课标中提到的10个核心词.

在求证S四边形ABCD＝S△ABF的结论时，实际上是将四边形的面积转化为三角形面积.在解题教学的过程中，我们常常要将四边形问题转化为三角形问题、将一般问题转化为特殊问题、将复杂问题转化为简单问题，借助已经获得的经验才能解决问题.

“问题情境”到“问题迁移”通过P是MN的中点这一线索，把“问题迁移”进行转化利用“问题情境”的结论和方法进行求解.而“实际应用”和“拓展延伸”都是直接利用或间接利用“问题迁移”的结论进求解.解决问题的过程中，是把四个问题看作一个整体，通过寻找它们之间的联系，进行类比、转化、迁移，充分体现了“数学整体认识及研究数学问题的方法”和“形成解决问题的一些基本策略”的课标理念，这是“数学”的方法，是重要的思维方式，体现继续学习的潜能.