单摆混沌现象的研究
李纪强,周斌,丁益民,2
(1.湖北大学物理学与电子技术学院,湖北 武汉 430062; 2.中国科学院理论物理研究所,理论物理国家重点实验室,北京 100190)
0 引言
单摆是物理学中一个很常见的模型,吸引了许多学者对其进行研究[1-6].伽利略最早发现了单摆振动的等时性,并用实验证明单摆的周期随摆长的二次方根变化.惠更斯第一次用单摆制作了摆钟,并从摆钟在南美洲比在巴黎每天慢2.5 min而推断这是由于地球自转引起的引力减弱导致的.牛顿用单摆证明了物体的重量总是与质量成正比.现在天文学中也常用单摆测量星体表面的重力加速度[7].由于单摆方程没有严格的解析解,在计算机诞生前,大多数讨论只限于小初始摆角的情况,对大角摆动仅用相图做了粗略的解释.本文中利用MATLAB软件严格求解单摆方程从而研究其混沌现象[8-11],通过数值分析的方法避免了其运动方程无严格解析解的问题.在对其现象进行模拟的同时,形象直观地呈现了单摆的周期、运动形式的演化与其参数的重要联系.基于单摆系统对初始条件的敏感依赖性,本文中在总结前人工作的基础上给出一种新的衡量混沌系统敏感性的量化指标——敏感系数,对研究非线性力学系统参数对运动形式演化的影响具有参考价值.
1 无阻尼的单摆
无驱动力、无阻尼的单摆的运动可由的方程(1)描述,其中θ为铅直方向与摆线的夹角,m为摆球质量,L为摆长,g为重力加速度.

(1)
整理得
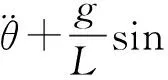
(2)
数学理论表明,方程(2)没有严格的解析解,一般的情况下,sinθ≈θ的近似不成立.利用数值分析中的龙格库塔法[12-13]可以求出方程(2)的数值解,参数取值为g=10 m/s2,L=1 m,m=1 kg.单摆的周期性运动的图像如图1所示.可以看出,与小角度摆动不同的是,初始摆角影响单摆的周期,且初始摆角越大,周期越长,当初始摆角为π时,单摆的周期趋于无穷大,即系统出现了相变现象.
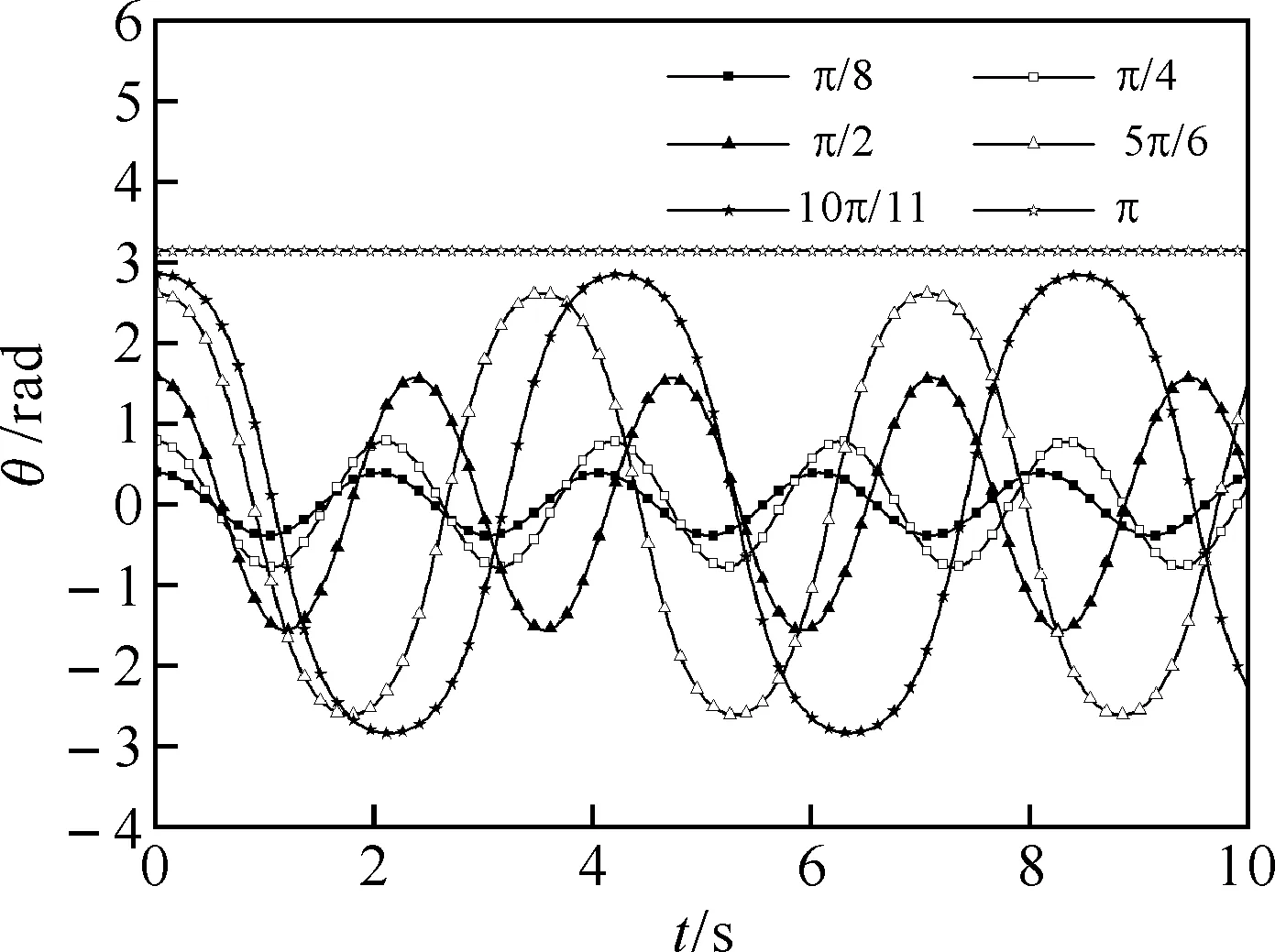
图1 不同初始摆角条件下单摆的运动图像
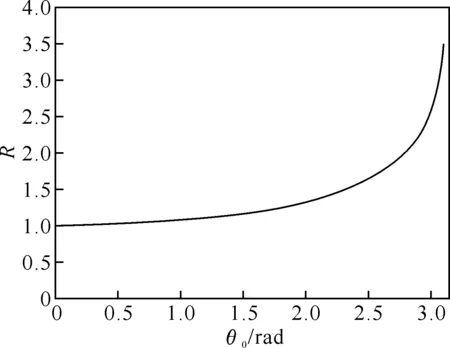
图2 周期比随初始摆角的变化

(3)

(4)
周期比随时间的变化如图2所示,可以看出初始摆角为π时,单摆的周期趋于无穷大,这与前面的结论吻合.
对混沌理论的研究中,用的比较多的是相图[15].对于单摆,由机械能守恒定律得

(5)
(6)
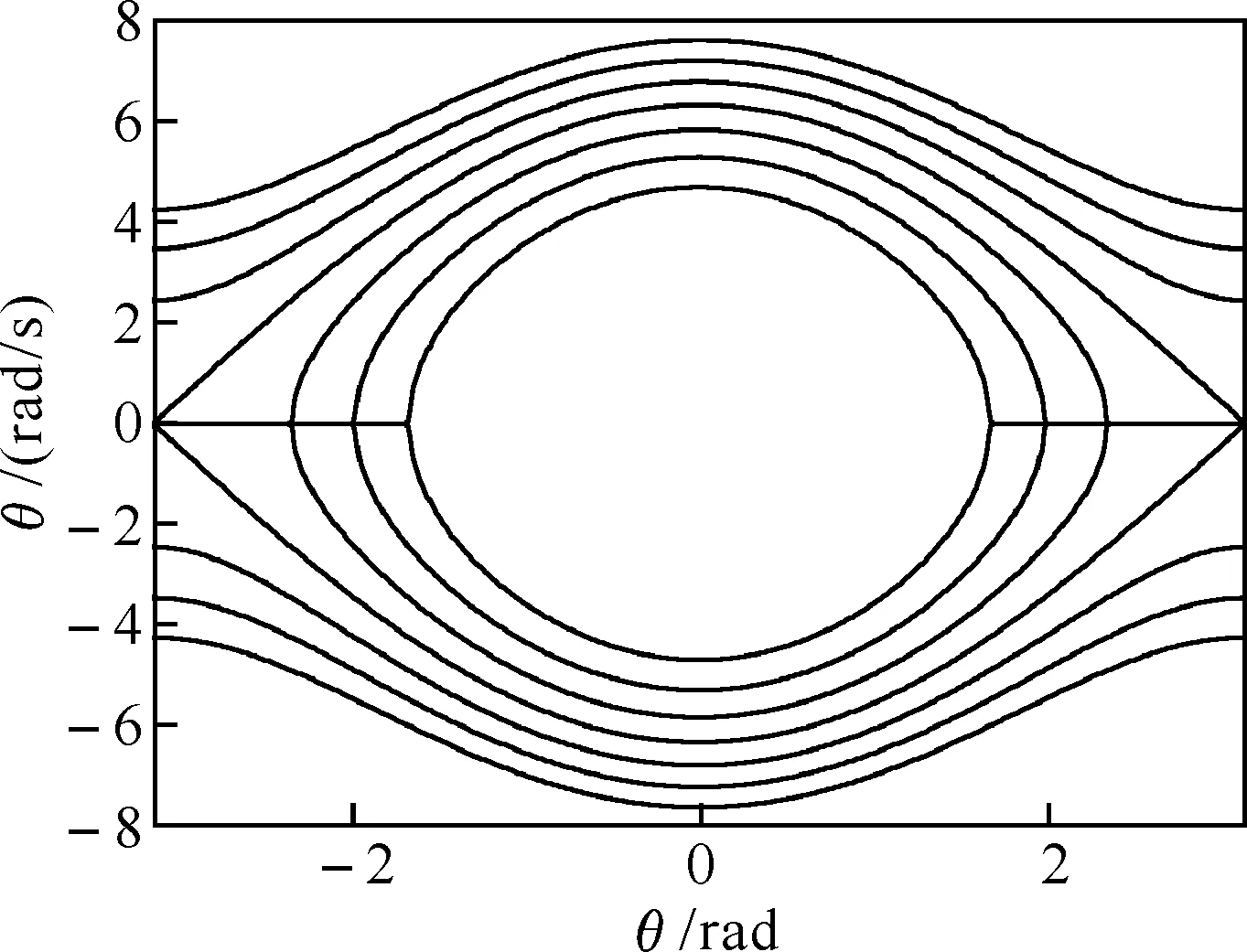
图3 1周期的相图
对于远离临界值的能量初值E,而后的运动是完全确定的,运动能够预测和重复,即能量初值“相同”则运动可以“重现”.当然,这里的“相同”指误差可以忽略不计,这类运动通常称为“规则运动”,对“规则运动”的研究确立了对牛顿力学“确定性”的认识.对于能量初值在临界值附近波动的运动,可能呈现出大为不同的情况.从相图上可以看出,如果能量初值略小于临界值,则运动遵从相图中闭合曲线的规律运动;而能量初值略大于临界值时,运动对应的相图中的曲线是非闭合的.在临界值附近一个微小的扰动能够造成结果的巨大差别.若δ是一个十分小的量以至于测量仪器测不出来,那么对能量E=2mgL+δ的初值都将认为是E=2mgL的初值,这时实验中将会观察到,对应“相同”的能量初值随着时间的变化有时演化成往复摆动,有时候演化成单向转动,运动出现了不可预测的“随机性”,单摆的这种“随机行为”称为混沌行为.
2 有阻尼的单摆
假设阻力与速度成正比,阻尼系数为γ,单摆的运动方程可写为:
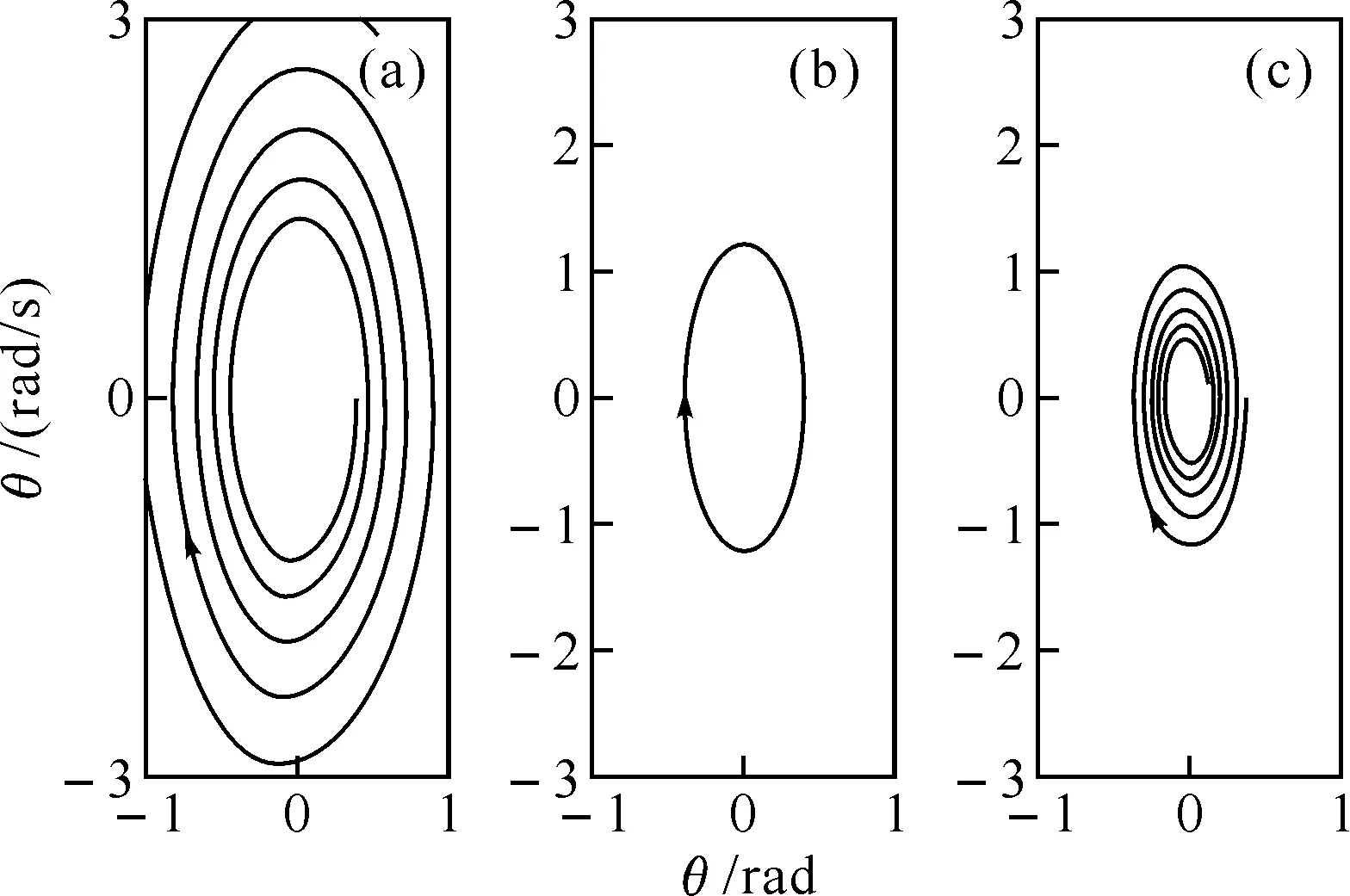
图4 单摆在(a)负阻尼,γ=-0.2 s-1;(b)无阻尼,γ=0;(c)阻尼,γ=0.2 s-1情况下的相图
(7)
可以分别画出单摆在负阻尼(γ=-0.2s-1)、无阻尼(γ=0)、阻尼(γ=0.2s-1)情况下的相图,此处初始摆角设定为θ0=π/8,如图4所示.可以看出,在负阻尼的状态下,系统的能量增加,单摆远离最初的平衡位置,又称“排斥子”.在无阻尼状态下,小角度单摆相轨迹是闭合的,单摆的状态可以确定.在阻尼状态下,由于能量的耗散,单摆的振幅越来越小,最后静止在平衡位置上,它的相轨迹为一条内旋的对数螺旋线,螺旋线中心是稳定的焦点,又称为“吸引子”[16-19].进一步研究可发现:混沌吸引子的图形虽然复杂,但它的结构具有稳定性,一般随着时间的增长,其轨线是不会重叠的,它是混沌系统中无序稳态的运动形态.具有无穷嵌套的自相似结构是混沌吸引子最典型的特征,如果取出吸引子中的一小部分进行放大,它将具有和原来吸引子相同的内部结构;若继续在其取出的一小部分中再取出一小部分继续放大,则它依然具有与原吸引子相同的内部结构,如此循环,以至无穷[20].
3 敏感性分析
混沌系统对初始条件的敏感依赖是混沌现象的特征之一,本文中对混沌现象中初始条件变化时产生的差异进行分析.以无阻尼单摆为例,固定参数为g=10 m/s2,L=1 m,m=1 kg.改变初始摆角,比较同一时间点单摆运动的θ值的差异.小角度情况下,方程(2)有较好的线性特征,结果有较好的预测性.在临界值θ0=π附近,初始条件较小的波动随时间的增加而被“放大”,结果差异很大,如图5所示.这种结果的波动作为将来时间的“初始条件”进一步被“放大”,所谓“差之毫厘,谬以千里”.为了描述单摆混沌现象对初始条件的敏感性,在参考他人的工作的基础上[21-22],本文中给出了一个量化的敏感性评价指标——敏感系数S.


图5 初始条件在临界值附近(0.97π<θ0<1.03π)时的单摆运动

图6 无阻尼单摆的敏感系数随初始摆角和摆长的变化

图7 无阻尼单摆的不同摆长条件下敏感系数随初始摆角的变化

图8 有阻尼单摆的敏感系数随初始摆角和阻尼系数的变化
4 结论
通过高精度的数值计算,严格求解无阻尼单摆和有阻尼单摆的运动方程,研究了单摆摆长、阻尼系数和初始摆角对单摆运动的影响.研究结果表明:单摆的周期与初始摆角有关;单摆在大角摆动时,系统的演化情况强烈依赖初始条件,不具有小角摆动的“可预测性”,它呈现出混沌行为.究其原因,大角摆动的运动方程不是一个线性微分方程,它的解不具有稳定性.通过计算敏感系数,发现初始摆角、单摆摆长、阻尼系数均能影响混沌系统的敏感性.
[1] Fulcher L P, Davis B F. Theoretical and experimental study of the motion of the simple pendulum[J]. Am J Phys,1976,44(1):51-55.
[2] Lima F M S, Arun P. An accurate formula for the period of a simple pendulum oscillating beyond the small angle regime[J]. Am J Phys,2006,74:892.
[3] Kidd R B, Fogg S L. A simple formula for the large-angle pendulum period[J]. Phys Teach,2002,40:81.
[4] Bender C M, Holm D D, Hook D W. Complex trajectories of a simple pendulum[J]. J Phys A: Math Theor,2007,40(3):F81.
[5] Antman S S. The simple pendulum is not so simple[J]. SIAM Rev,1998,40(4):927-930.
[6] Qing X Y, Pei D. Comment on approximation for a large-angle simple pendulum period[J]. Eur J Phys,2009,30(5):L79.
[7] Parks H V, Faller J E. Simple pendulum determination of the gravitational constant[J]. Phys Rev Lett,2010,105(11):110801.
[8] Liu Z H, Zhu W Q. Homoclinic bifurcation and chaos in simple pendulum under bounded noise excitation[J]. Chaos, Soliton Fract,2004,20(3):593-607.
[9] Humieres D, Beasley M R, Huberman B A, et al. Chaotic states and routes to chaos in the forced pendulum[J]. Phys Rev A,1982,26(6):3483.
[10] Blackburn J A, Zhou J Y, Vik S, et al. Experimental study of chaos in a driven pendulum[J]. Phys D: Nonlinear Phenomena,1987,26(1):385-395.
[11] Kadanoff L P. From periodic motion to unbounded chaos: investigations of the simple pendulum[J]. Phys Scripta,2007,1985(T9):5.
[12] Butcher J C. The numerical analysis of ordinary differential equations: Runge-Kutta and general linear methods[M]. New York: Wiley Int Sci,1987.
[13] Jameson A, Schmidt W, Turkel E. Numerical solutions of the Euler equations by finite volume methods using Runge-Kutta time-stepping schemes[J]. AIAA,1981,1259:1981.
[14] 陈文涛,龚善初.单摆振动分析[J].湖南理工学院学报:自然科学版,2008,21(1):68.
[15] Matthews P C, Strogatz S H. Phase diagram for the collective behavior of limit-cycle oscillators[J]. Phys Rev Lett,1990,65(14):1701-1704.
[16] Lorenz E N. Deterministic nonperiodic flow[J]. J Atmos Sci,1963,20(2):130-141.
[17] Brandstater A, Swinney H L. Strange attractors in weakly turbulent Couette-Taylor flow[J]. Phys Rev A,1987,35(5):2207.
[18] Ott E. Strange attractors and chaotic motions of dynamical systems[J]. Rev Mod Phys,1981,53(4):655.
[19] Grassberger P, Procaccia I. Characterization of strange attractors[J]. Phys Rev Lett,1983,50(5):346-349.
[20] 王海红,傅廷亮,李菊芳.分形和混沌系统的仿真[J].吉首大学学报:自然科学版,2012,33(4):46-48.
[21] Kolyada S F. Li-Yorke sensitivity and other concepts of chaos[J]. Ukr Mat J,2004,56(8):1242-1257.
[22] Blümel R. Exponential sensitivity and chaos in quantum systems[J]. Phys Rev Lett,1994,73(3):428-431.

