图的符号边控制与减边控制

徐保根，操叶龙，康洪波，赵利芬

（华东交通大学基础科学学院，江西南昌330013）

1 引言及定义

本文中所指的图均为无向简单图，文中未说明的符号和术语同于文献［1］。

设G=(V，E)为一个图，e∈E，则NG(e)表示G中与e相邻的边集，称为e的边邻域，NG[e]=NG(e)∪{e}为e的闭边邻域。(e)=|NG(e)|表示e在G中的边度。NG(e)和NG[e]可分别简记为N(e)和N[e]。若e=uv∈E(G)，则有d(e)=d(u)+d(v)-2。

近几年来，图的控制理论研究的内容越来越广泛，各类控制概念相继产生且研究成果不断丰富，T.W.Haynes等人的专著［2］综述了近几些年来图的控制理论研究方面的主要研究成果。然而，它们绝大多数均属于图的点控制，很少涉及到关于图的边控制问题和结果。2001年徐保根［3］首先提出了图的符号边控制概念，获得了符号边控制数的许多界限，并将这一概念推广到边上的多种符号控制，如符号星控制、符号圈控制、符号团控制、符号路控制等等。同样地，这也产生了对应的减边控制概念，从而使得控制理论研究内容和研究成果越来越丰富，徐保根专著［4］综述了这些研究成果。

定义1.1［3］设G=(V，E)是一个非空图，一个函数f:E→{- 1，+1} ：如果满足f()≥1 对每一条边e∈E(G)均成立，则称f为图G的一个符号边控制函数。图G的符号边控制数记为(G)，定义(G)=min｛f(e)|f为G的一个符号边控制函数｝。并且对于空图G=，则定义(G)=0。

定义1.2［5］设G=(V，E)为一个非空图，一个函数f:E→{-1，0，+1}被称为图G的一个减边控制函数，如果对于G中每一条边e均有f()≥1成立。图G的减边控制数定义为(G)=min｛f(e)|f为图G的减边控制函数｝，对于空图G=，则同样定义(G)=0。

比较上述两个定义不难看出，图G每一个符号边控制函数均为G的一个减边控制函数，从而有下面的引理1.1。

引理1.1对任意图G，均有m(G)≤s(G)成立。

对于图的符号边控制数，目前人们已获得了许多界限，文献［3］中我们确定了一个具有m条边的简单图的最小符号边控制数，即下面的引理1.2。

引理1.2［3］设m≥1，ψ(m)表示m条边图的最小符号边控制数，则有

由此引理，直接可得下面的引理1.3。

引理1.3对任意图G，若|E(G) |=m≥1，则有

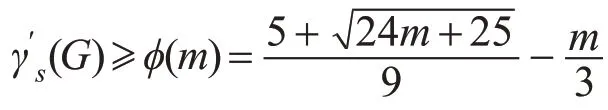
引理1.4［5］对任意图G，若δ(G)≥1，则s(G)≥|V(G)| -|E(G) |，且此下界是最好可能的。

虽然人们已获得了符号边控制数的众多下界，由引理1.1知，这些下界均不能作为减边控制数的下界，可见本文探讨减边控制数的下界是非常有意义的。此外，在现有的关于(G)的界限中，几乎都是依赖于图的阶数、边数、最大度和最小度，本文给出其依赖于边度序列的界限，并利用导出子图，通过(G)的下界来确定m(G)的下界。

2 主要结果及其证明

前面介绍了图的边度概念，一条边e∈E(G)的边度是指在图G中与e相邻的边数。对于一个非空图G，若|E(G) |=m≥1，自然有边度度序列()存在。同图的（点）度序列一样，图的边度序列常记为，即按边度的大小进行排列。

设G=(V，E)为一个非空图，S⊆E，f为图G的一个符号边控制函数或减边控制函数，为了方便，在本文中我们记f(S)=f(e)。

定理2.1对任意图G，若|E(G) |=m≥1且为其边度序列。

令k0=min，则有(G)≥2k0-m。

证明设f为图G的一个符号边控制函数，且使得(G)=f(E)。由定义1.1知，对于每一条边e∈E，均有f(N[e])≥1，故f(N[e])≥m，从而有

令：P={e∈E|f(e)=+1} ，M={e∈E|f(e)=-1} ，|P|=t，故有 |M|=m-t。

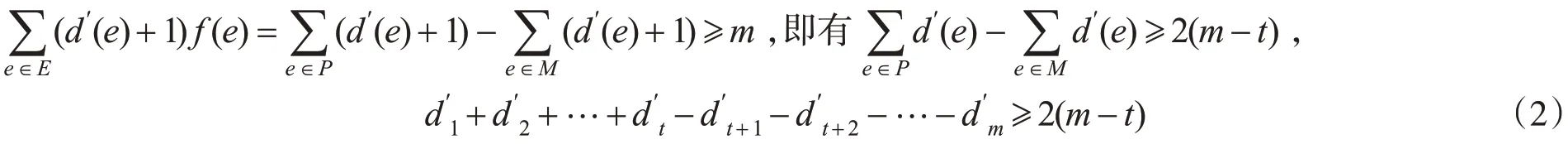
将k0的定义与（2）式比较得t≥k0，因此，(G)=2t-m≥2k0-m，定理证毕。

推论2.1对任意n阶r-正则图G，均有(G)≥。

证明由于G为一个n阶r-正则图，易见=2r-2(1 ≤i≤m)，由k0的定义中得到(2r-2)k-(2r-2)(m-k)≥2(m-k)，故k≥m=，因此，k0≥。

下面考虑图的减边控制数。与定理类似地可得到下面的结论。

定理2.2对任意图G，若|E(G) |=m≥1且d′1 ≥d′2 ≥…≥d′m为其边度序列。

则γ′m(G)≥min。

证明设f为图G的一个减边控制函数，且使得(G)=f(E)。由定义1.2 知，对于每一条边e∈E，均有f(N[e])≥1，故f(N[e])≥m，从而有

令：P={e∈E|f(e)=+1} ，M={e∈E|f(e)=-1} ，Q={e∈E|f(e)=0} ，|P|=s，|M|=t，|Q|=m-s-t。由（3）式得

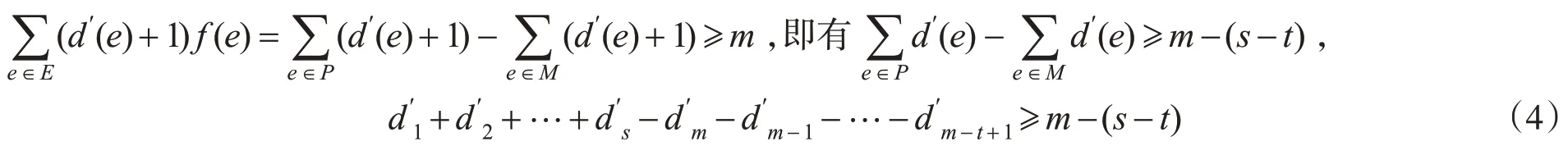
推论2.2对任意n阶r-正则图G，均有(G)≥。

证明由于G为n阶r-正则图，故=2r-2(1 ≤i≤m)，代入定理2.2中得出(2r-2)(s-t)≥m-(s-t)，故s-t≥，由定理2.2，推论2.2成立。

下面用一个图G的所有子图的最小符号边控制数来表达G的减边控制数的下界。若H为图G的一个子图，则用H⊆G来表示。

定理2.3对任意图G，令π(G)=min{(H)|H⊆G} ，则(G)≥π(G)。

证明设f为图G=(V，E)的减边控制函数且使得(G)=f(E)，令X0={e∈E|f(e)=0} ，G0=G-X0

可见f0=为图G0的一个符号控制函数，由于G0为G的子图，从而有(G)=f(E)=f0(E(G0))≥γs(G0)≥π(G)，定理证毕。

由上述定理2.3可见，一个图G的减控制数不小于其所有子图的最小符号控制数，因此有下面的结论。

定理2.4如果存在一个递减函数φ(t) ，使得对任意正整数t和任意具有t条边的图H，均有(H)≥φ(t)成立，则对任意具有m条边的图G，均有(G)≥φ(m)。

证明根据定理2.3，存在H⊆G，使得(H)=π(G)。令|E(H)| =r，故r≤m。

上述定理2.4告诉我们，如果找到了一个对任意m条边的图G都成立的的下界φ(m)，且φ(m)为m的递减函数，则φ(m)也可作为的下界。

根据引理1.3，且注意到φ(m)=为一个关于m的递减函数（m为非负整数），故由定理2.4可直接得到下面的定理。

定理2.5对任意一个具有m(m≥1)条边的图G，均有(G)≥φ(m)=。

3 若干注记

定义3.1设φ=φ(G)是一个包含图G的若干参数的解析式，如果对任意图G的任意子图H⊆G，均有φ(H)≥φ(G)成立，则称φ为图的减性表达式，反之为增性表达式。

根据定理2.3，可将定理2.4推广为如下的结论。

定理3.1如果存在一个关于图的减性表达式φ，使得对任意图H，均有(H)≥φ(H)成立，则对任意图G，均有m(G)≥φ(G)。

猜想对任意图G，若δ(G)≥1，则有m(G)≥|V(G) |-|E(G) |。

值得注意的是，类似的方法也可用在点控制中，参见文献［7］，或许还可用在符号全控制中［8］及反符号边控制［9］，这有待于进一步的研究。

［1］帮迪J A，默迪V S R.图论及其应用［M］.上海：科学技术出版社，1984：5-35.

［2］HAYNES T W，HEDETNIEMI S T，SLATER P J.Domination in Graphs［M］.New York：Marcel Dekker，Inc.，1998：32-41.

［3］BAOGEN XU.On signed edge domination numbers of graphs［J］.Discrete Math，2001，239：179-189.

［4］徐保根.图的控制理论［M］.北京：科学出版社，2008：130-153.

［5］BAOGEN XU.Two classes of edge domination in graphs［J］.Discrete Appl Math，2006，154：1541-1546.

［6］BAOGEN XU.On edge domination numbers of graphs［J］.Discrete Math，2005，294：311-316.

［7］BAOGEN XU.On minus domination and signed domination number in graphs［J］.J of Math Res and Exposition，2003（4）：586-590.

［8］赵金凤，徐保根. On signed edge total domination numbers of graphs［J］. J of Math Res and Exposition，2011，32（2）：209-214.

［9］徐保根.关于图的反符号边控制［J］.华东交通大学学报，2007，24（5）：144-147.