数学思维品质培养的案例教学

任俊红

（安徽省合肥市巢湖第一中学，安徽 合肥 238000）

数学思维品质培养的案例教学

任俊红

（安徽省合肥市巢湖第一中学，安徽 合肥 238000）

思维与数学学习关系密切，因此培养学生的数学思维能力是提高数学效益的关键。良好的数学思维平直有利于减轻当下中国中学生学习数学的负担，提高其学习数学的效率，因而具有重要的意义。本文就如何对数学思维品质的培养进行研究并结合课堂实践给出了案例分析。

思维品质；深刻性；广阔性；创新性；批判性

数学教育的主要任务就在于使学生形成完善的思维结构，并借助于这种结构掌握数学知识，提高数学能力。数学思维的教学功能也被越来越多的教师重视，新的数学教学大纲把数学思想方法纳入基础的知识范畴是落实数学素质教育的重大举措。在数学教学中向学生展示获取知识、技能及解决问题的思维品质之目的，创造了“客观”基础，提供了可能，才能使学生终身受益。本文试举几例说明，以供参考。

一、挖掘数学表达式的内涵，发掘思维的深刻性

思维的深刻性是指思维活动的抽象程度和逻辑水平以及思维活动的深度。它集中的表现为能透过表面现象和外部联系，深刻地理解概念，抓住概念定理的核心及内在联系，准确地掌握概的内涵及使用条件和范围。揭示问题规律的一个由感性到理性的思维过程。从特殊到一般进行联想，是培养这一深刻的一个重要方面。

所以z2/y+y2/z+z2/x≥x+y+z（当x=y=z时取等号）

在证出后，可引导学生探索一般的规律，对多个正数是否也有（1）成立呢？

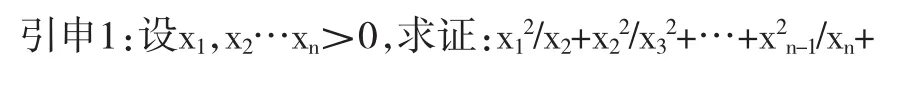
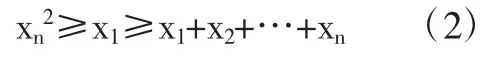
事实上，按证（1）的方法以，同理可证（2），还可进一步思考：对（2）式我们发现左边各项的分线具有一种特殊的顺序。此时可问，分母不具备这种顺序是否也有同样的结论？

引申2：设y1·y2…yn＞0，x1·x2…xn＞0且x1+x2+…+xn=y1+y2+…+yn

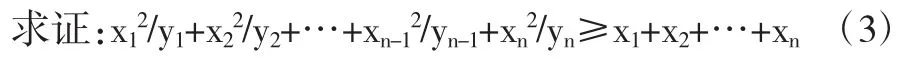
这样使问题层层深入，思维不断深化。数学思维的深刻性表现在：善于洞察数学对象的本质属性与相互联系，能捕捉矛盾的特殊性，从研究材料中发现最有价值的因素。能迅速确定解题策略和各种方法，模式等。在教学中抓住以下几个过程：（1）对各种数学材料整理的概括过程。（2）对有关数学概念背景，内涵，外延认识的深化过程。（3）对具体数量关系与空间形式的抽象过程。（4）对基本数学观点与方法的总结过程。

二、多角度思考、探索，培养思维的广阔性

思维的广阔性是指思维活动作用的广泛和全面的程度，它集中表现为思路宽广，能从众多的知识领域和多方面的知识出发，全面的考察问题，作出广泛的联想，多角度、多层次、多方位的观察与思考。在广泛的范围内寻求解法，是思路开阔而全面的思维品质。在数学学习中，应要求学生既把握数学问题的整体，抓住它的基本特征，又要求不忽略重要的细节和特殊的因素，放开思路进行思考，解决问题。

分析：观察待证不等式的结构，抓住其形式特征。

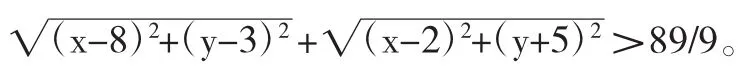
多向地进行联想，从不同的角度沟通，联系就得：

联想1：不等式左边看成动点p（x，y）到两定点A（8，3）.B（2，-5）的距离之和.由=10。

联想2：以动点到两点距离之和为线索，联想到椭圆的定义，视长轴2a可变，即2a为参数。令=10且椭圆中2a＞2c故结论成立。

联想3：向量模的形式与题给不等式左边有相似性，故想到可用向量不等式证明，即令有

但红江橙的发展之路却并不平坦。陈树华为我们回忆了几代红江橙园的命途多舛：“1993年，黄龙病蔓延，两万多亩橙树全部毁灭。1997年种了300多亩，2003、2004年又开始不行了……红江人不死心啊，从来没有放弃过！”

联想4：由联想3易想到可用复数去证明。可令：

z1=（x-8）+（y-3）i，z2=（x-2）+（y+5）i。则|z1|+|z2|≥|z1-z2|=|-6-8i|=10这几种联想证明既简洁，又具有独到之处，如果经常这样训练，对开阔学生思路，活跃学生思维大有裨益。另在数学教学中，为了培养学生思维的广阔性，还可以建构观，形象的心智图像，使抽象问题具体化，隐性问题显性化。

例3.已知△ABC中，角A.B.C的对边分别是a，b，c。且B=2C求证：b2=c（a+c）。

这是我在教学过程中遇到的一道习题，利用解三角形的知识可以证明，接着利用直观，形象的心智图像。有如下解法：

方法1（图1）：如果把b2=c（a+c）看成b/c=（a=c）/b，则会出现“相似三角形”的形象。

方法2（图2）：如果把b2=c（a+c）看成b·b=（a+c）·c，则会出现“相交弦定理”的心智图像。

方法3（图3）：如果把b2=c（a+c）的特点，也会联想到“圆的切割线定理”。

从以上几个方面进行分析，学生当时大为感叹！不但提高学生的听课兴趣，而且能使初高中的数学知识得以衔接。

数学思维的广阔性主要体现在：一题多解，一题的多种解释，加强变式训练。选择典型问题，或从条件入手，或从结论入手进行变迁，得到一系列结构相互联系，解题思路逐步深入的题组。所以教师在教学过程中对学生思维广阔性的培养应注重在“一题多变”上进行，这样既开拓了学生的思路，巩固了学生的知识，还可以激发学生学习的积极性，提高了他们学习数学的兴趣。

图一

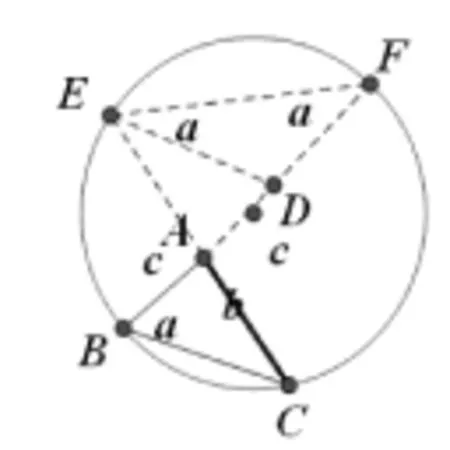
图二

图三

三、广泛联想，发挥想象力，活跃数学创新思维

在数学教学中，应重视对学生联想思维的训练，能将定议或属性相距甚远的两个事物联想起来思考，打开思维的通道，突破思维的定式。教会学生分析、观察、类比，引导学生学会转化，掌握联想法则，把学生思维的变式、发展、求异等优秀的思想品质在解题中落到实处。培养学生大胆猜想，勇于探索，严谨求实的创新思维。

在高中数学教材p16，有这样的不等式：

例4.求证：（ac+bd）2≤（a2+b2）（c2+d2）。

再介绍运用比较法，分析法，综合法后，引导学生进一步思考。

思考1：如果把不等式两边乘以4，与判别式b2≤4ac类似，由此可构造二次函数f（x）=（a2+b2）x-2（ac+bd）x+（c2+d2）=（ax-c）2+（bx-d）2≥0

从而Δ≤0即证。

思考2：如果把不等式两边同开方，可想到向量的模。

在中学，思维的创新性更多表现在发生矛盾以后，把知识融会贯通，以进攻的姿态，突破矛盾，最终解决问题。在平面向量的教学中，学生向我求解这样一道习题。

例5.求证：sin0+sin（2π/n）+sin（4π/n）+sin（6π/n）+…+sin（2n-2）π/n=0。

分析：该题纯从三角去考虑，是较烦琐的。如果想到单

位圆上的点A（kcos2kπ/n·sin2kπ/n）。而点Ak又对应着向量命题转化为即可。又向量可视为力fk进而想到大小一样终端分布在正n边行的n个顶点上的共点于正n边行中心的力系其合力为零。故所以sin0+sin（2π/n）+sin（4π/n） +sin（6π/n）+…+sin（2n-2）π/n=0且cos0+cos（2π/n）+cos（4π/n）+…+cos（2n-2）π/n=0证明（略）用数学方法解决物理总是似乎理所当然，但反过来用物理方法去解决数学问题是不太被人们重视，但对有些问题这样去做不仅解法新颖，具有创新性，而且强化了各科之间的相互联系、相互渗透，这无疑是为培养思维创新性的优良品质提供锻炼机会。

四、培养思维的批判性

思维的批判性是指思维活动中善于严格地估计思维材料和精细地检查思维过程。在数学教学中，学生思维的批判性表现为愿意进行各种方式的检验和反思。对已有的数学表述或论证能提出自己的看法，不是一味盲从，思想上完全接受了东西，也要谋求改善提出新的想法和见解可从这几方面入手：（1）培养学生解题后的反思习惯，就是培养学生对解题活动进行回顾，思考，总结，评价，调节也就是对经验和教训的反思。（2）教学中经常进行改错训练，教学中教师经常出一些改错题，让学生讨论改正，有助于学生形成思维的批判性。（3）教学中经常提倡学生不要迷信书本，不要迷信老师，要有自己的独立思考，敢于提出不同的见解。总之，思维品质的培养是一个长期的过程，不能立竿见一蹴而就，它艰巨而复杂。在教学中引导学生对问题的直觉感悟、探索、猜想、证明，培养学生的科学精神，创新能力，形成良好的数学思维习惯和用数学的意识，感受数学创造的乐趣，增进学好数学的信心，获得对数学较为全面的体验和理解，为培养学生综合运用知识，解决问题提供机会。

[1]曹才翰，章建跃.中学数学教学概论[M].第二版.北京：北京师范大学出版社，2008.

[2]朱应声.复数教学中数学思想方法的培养[J].数学教学，1989，（02）.

[3]刘辉.中考数学综合题解题指导[J].学生之友（初中版）（中考），2009，（04）.

[4]邱宗如.剖析线性规划试题所渗透的数学思想方法[J].福建中学数学，2010，（07）.

[5]孙秀荣.数学教学要注重渗透数学思想方法[J].赤峰教育学院学报，2003，（02）.

[6]宁连华，等.心智图象对问题解决的认识功能探析[J].中学数学杂志，2011，（03）.

[5]王子忻.数学教学方法[M].北京：高等教育出版社，2008.

[6]王万军.学习解题改错心理浅析[J].中学数学研究，2011，（05）.

G633.6

A

1674-9324（2014）04-0113-03

任俊红（1977-），男，安徽无为人，中学教师。