关于不定方程x3＋8＝61y2的整数解

王 龙

（陕西广播电视大学延安分校，陕西延安716000）

关于不定方程x3＋8＝61y2的整数解

王 龙

（陕西广播电视大学延安分校，陕西延安716000）

利用递归数列和同余式的相关性质证明了不定方程x3＋1＝122y2仅有整数解（x，y）＝（－1，0），然后证明了不定方程x3＋8＝61y2仅有整数解（x，y）＝（－2，0）。

不定方程；递归数列；同余式；整数解

不定方程

（其中：D是无平方因子的正奇数）是一类基本而重要的Diophantine方程。文献［1］证明了当D是奇素数时，如果D＝3，则方程（1）仅有整数解（x，y）＝（11，±21）。文献［2］证明了不定方程x3－8＝7y2仅有整数解（x，y）＝（2，0）。对于不定方程x3± 1＝Dy2（D＞0）也有不少作者进行了研究。文献［3］给出了x3＋1＝13y2仅有整数解（x，y）＝（－1，0），文献［4］证明了x3＋1＝14y2有整数解（x，y）＝（－1，0），（5，±3），文献［5］证明了当D＝301时，不定方程x3－1＝Dy2（D＞0）仅有整数解（x，y）＝（1，0），文献［6］也给出了x3＋1＝7y2有整数解。

受到以上文献的启发，本文用递归数列与同余式的相关性质首先证明了不定方程x3＋1＝122y2仅有整数解（x，y）＝（－1，0），接着利用这一结果和以上知识点证明了不定方程x3＋8＝61y2仅有整数解（x，y）＝（－2，0）。

1 相关引理

引理1［7］4x4－3y2＝1有整数解（x，y）＝（1，1），（－1，－1），（1，－1），（－1，1）。

引理2［7］x2－3y4＝1有整数解（x，y）＝（2，1），（7，2），（1，0），（－1，0）。

引理3不定方程

只有整数解（x，y）＝（－1，0）。

证明：因为（x＋1，x2－x＋1）＝1或3，所以方程（2）式给出以下4种可能的分解。

因为61≡5（mod8），如果2｜z，那么x≡－1（mod8），从而3≡5w2（mod8），这是不可能的。如果2｜z，那么x≡1（mod8），从而1≡5w2（mod8），这也是不可能的。因此这种情况无解。

由x2－x＋1＝w2解得x＝0，1，这两种情况都不符合x＋1＝122z2。因此这种情况无解。

因为61≡5（mod8），如果2｜z，那么x≡－1（mod8），从而3≡7w2（mod8），显然这是不可能的。如果2｜z，那么x≡1（mod8），从而有1≡7w2（mod8），这也是不可能的。因此这种情况也无解。

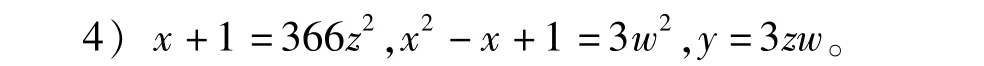
x2－x＋1＝3w2可化为把x＋1＝366z2代入上式得（2w）2－3（244z2－1）2＝1。于是有

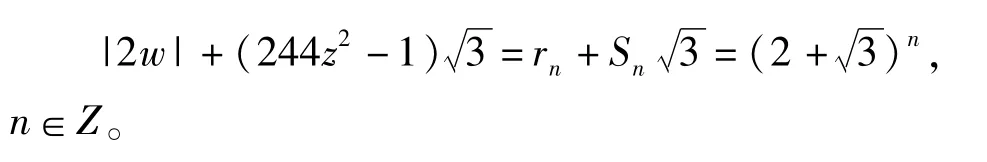
所以有

因为2｜n时，2｜Sn，但是（3）式不可能成立。

若n≡1（mod4），Sn≡1（mod8），可得出244z2≡2（mod8），这也是不可能的。因此只需考虑n≡－1（mod4）的情况。

令n＝4m－1，有

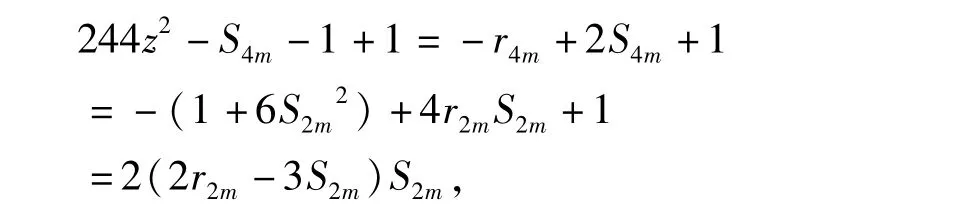
因此有244z2＝r2mS2m。

又由于

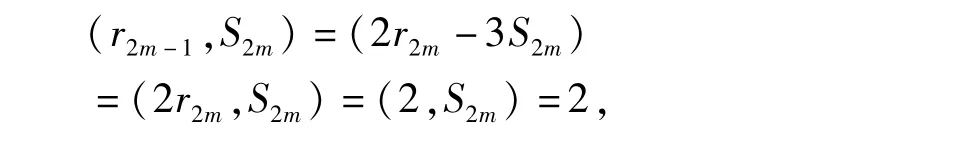
则有

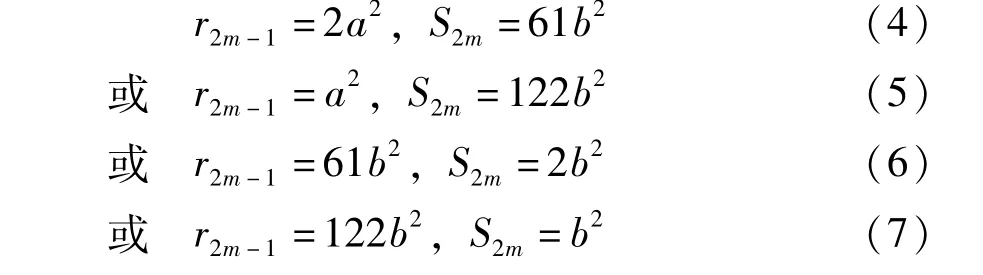
其中z＝ab。

根据引理1可知，（8）式有整数解（a，S2m－1）＝（1，1）或（1，－1）或（－1，1）或（－1，－1）。从而有S2m－1＝±1，即m＝0或1。

当m＝1时，不满足（4）式中的S2m＝61b2，因此m≠1。当m＝0时，S2m＝61b2得b＝0，从而z＝0，代入情形4）中得平凡解为（x，y）＝（－1，0）。

因为2｜z时，rn≡2（mod4）可得（5）式和（6）式的第一个式子不成立，因此可排除（5）和（6）的这两种情况。

由（7）中S2m＝b2可得

由引理2知（9）式有整数解（r2m，b）＝（2，1）或（7，2）或（1，0）或（－1，0）。但2｜S2m，由（7）得2｜b2，因此b＝2或0。

当b＝0时，也即S2m＝0，得m＝0与r2m－1＝122b2矛盾，因此b≠0。当b＝2时，S2m＝4，即m＝1与r2m－1＝122b2矛盾，因此b≠2，故而（7）这种情况无解。

所以，情形4）给出平凡解（x，y）＝（－1，0）。

综合上述4种情况的解述，得出不定方程x3＋1＝122y2只有整数解（x，y）＝（－1，0）。

2 主要结论及证明

定理不定方程

仅有整数解（x，y）＝（－2，0）。

证明：若x≡0（mod2），由（10）式得出y≡0（mod4）。故而方程（10）可化为由引理3可知，x3＋1＝122y2仅有整数解（x， y）＝（－1，0），此时方程（10）有整数解（x，y）＝（－2，0）。

若x≡1（mod2），此时（x＋2，x2－2x＋4）＝1或3，因此（10）式给出下列4种可能的分解情况：

情形1：x＋2＝183u2，x2－2x＋4＝3v2，y＝3uv；

情形2：x＋2＝61u2，x2－2x＋4＝v2，y＝uv；

情形3：x＋2＝3u2，x2－2x＋4＝183v2，y＝3uv；

情形4：x＋2＝u2，x2－2x＋4＝61v2，y＝uv。

下面分别讨论这4种情形给出的（10）式的整数解。

情形1 由x2－2x＋4＝3v2化简有3v2－（x－1）2＝3，将x＋2＝183u2代入得到v2－3（61u2－1）2＝1，所以有

61u2－1＝Sn，n∈N。

容易验证下列式子成立：

因为x≡1（mod2），所以u≡1（mod2），Sn≡0（mod2），从而n≡0（mod2）。

当n≡0，2（mod4）时，有Sn≡0，4（mod8）。由61u2－1＝Sn有61u2≡3，7（mod8）。所以5u2≡3，7（mod8），这显然不可能，故该情况下（10）式无整数解。

情形2 由x2－2x＋4＝v2得出x＝2，0，这两个解均不符合式x＋2＝61u2，故该情形下（10）式无解。

情形3 将x2－2x＋4＝183v2化解为（x－1）2－183v2＝－3，将x＋2＝3u2代入得到3（3u2－3）2＋3＝183v2，化简即61v2－3（u2－1）2＝1。

根据文献［8］有

O156.1

A

1004－602X（2014）03－0004－03

10.13876/J.cnki.ydnse.2014.03.004

2014-06-20

王 龙（1981—），男，陕西延安人，陕西广播电视大学延安分校讲师。