TTI介质相速度对弹性模量参数的敏感性研究
黄光南,刘 洋,李红星,张 华,李泽林
(1.东华理工大学放射性地质与勘探技术国防重点学科实验室,江西南昌330013;2.中国石油大学(北京)油气资源与探测国家重点实验室,北京102249;3.中国石油大学(北京)CNPC物探重点实验室,北京102249)
各向异性现象在地下介质中普遍存在,室内研究和野外观测表明大多数岩石存在明显的各向异性性质。引起岩石各向异性性质的主要因素有:岩石的颗粒排列、晶格结构、薄层叠加、裂隙裂缝以及方向应力[1-4]。由于地震波在各向同性介质与各向异性介质中传播的差异性,地震数据的处理、解释和反演必须考虑到岩石的各向异性性质,如果仍然延用各向同性介质的假设,可能会导致一些错误的处理和解释结果。从地球物理反演角度分析,敏感性是指模型参数产生一个微小扰动量时,对应观测数据的变化大小。速度反演通常利用雅克比矩阵对当前模型不断更新,雅克比矩阵的元素一般是偏微分算子,这个偏微分算子就是速度敏感函数。如果某个弹性参数对应的速度敏感函数很灵敏,则经过几次迭代就可以得到正确的反演结果;相反,如果该弹性参数对应的速度敏感函数不灵敏,则无论经过几次迭代反演都很难得到正确的反演结果。
关于各向异性介质速度敏感函数的计算方法,Every等[5]、Chapman等[6]和Zhou等[7]分别做了大量的研究工作。1992年,Every等在研究各向异性介质的弹性参数时,将弹性参数刚度矩阵分解成各向同性介质弹性参数矩阵与各向异性介质扰动量矩阵之和,并且通过求解特征方程得到了纵波相速度表达式,纵波相速度表达式对弹性参数求偏微分得到了敏感性系数。1996年,Chapman等对各向异性介质的速度敏感函数做了研究,利用“固定图钉法”原理分析了qP波和qSV波在介质对称轴倾角为0,45°和90°方向的速度值。在此基础之上,给定各向异性介质参数一个扰动量,分析qP波和qSV波在0,45°和90°方向的相速度变化大小。2005年,Zhou等基于VTI介质模型对速度敏感函数进行了详细研究,分别利用特征值法与特征向量法求取了速度敏感函数表达式,其中特征值法包括相速度偏微分表达式和群速度偏微分表达式。
分析可知,上述学者们所做的研究工作尚存在一些不足之处。Every等推导出的敏感性系数表达式是从材料科学的角度提出的,表达式极其复杂,所以缺乏实用性。Chapman等推导的相慢度扰动量表达式非常有意义,但是该表达式只能针对特定的几个角度,未能描述不同观测角度时相慢度扰动量的变化。Zhou等推导的速度敏感函数是基于VTI介质模型,其中速度敏感函数的群速度偏微分表达式非常复杂,在实现各向异性走时反演时比较困难。
参考前人基于VTI介质模型的速度敏感函数计算方法,我们推导了基于TTI介质模型以相速度偏微分表达的速度敏感函数计算方法。针对层间块状异常体模型,分别对背景介质与异常体介质计算qP,qSV和qSH波的速度敏感函数,同时分析VTI介质和TTI介质情形下不同波模式的速度敏感函数特性。为了验证TTI介质速度敏感函数计算方法的正确性,利用TI介质反射波非线性走时反演算法对层间块状异常体模型进行了走时反演。
1 TTI介质速度敏感函数计算方法
1982年,Cerveny等[8]提出了各向异性介质一阶走时扰动方程,很多学者提出的地震走时反演表达式都是对该方程的演化[9-11]。Zhou等[12]推导出了走时扰动方程的3种表达形式,其中相对简单的是一阶走时扰动方程的相速度偏微分表达式:
(1)
式中:c和U分别为各向异性介质的相速度和群速度;av∈{a11,a13,a33,a44,a66,θ0,φ0}为各向异性介质模型的弹性参数、对称轴倾角和方位角。由公式(1)可以看出,相速度的偏微分(∂c/∂av)是各向异性介质走时扰动方程的重要组成成分,对各向异性介质走时反演至关重要。
速度敏感函数是相速度(或群速度)对各向异性介质参数的偏微分表达式。由于群速度是相速度的函数,所以利用相速度偏微分表达速度敏感函数更加简便。我们基于TTI介质模型推导相速度对介质弹性模量参数的偏微分表达的速度敏感函数计算方法。
TTI介质模型由5个弹性参数(a11,a13,a33,a44,a66)或者Thomsen参数(α0,β0,γ,ε,δ*)来定义。基于描述各向异性介质中地震波传播运动学特性的克里斯托夫方程,在TTI介质中克里斯托夫矩阵的特征值,即相速度的表达式也可以写成如下形式[13]:
(2)
其中,P和Q的表达式为
(3)
Q1,Q2和Q3的表达式为
(4)
式中:ϑ为相慢度向量n和TTI介质对称轴ez′之间的夹角。n=(sinθcosφ,sinθsinφ,cosθ);ez′=(sinθ0cosφ0,sinθ0sinφ0,cosθ0);θ和φ分别为相慢度向量n的倾角和方位角,θ从垂直向下的z轴方向开始测量,φ从水平方向的x轴方向开始测量;θ0和φ0为TTI介质对称轴的倾角和方位角。将(3)式和(4)式代入(2)式并对av∈{a11,a13,a33,a44,a66,θ0,φ0}求偏导数,得到3个相速度c1,c2和c3对TTI介质弹性模量参数的偏微分表达式:
(5)

(6)

(7)
由TTI介质的对称轴向量与相慢度向量之间的关系,可以计算出两个向量之间的夹角和夹角的余弦表达式:
(8)
(9)
将(6)式、(7)式和(9)式逐一代入(5)式,即可以得到相速度c1,c2和c3对TTI介质弹性模量参数av∈{a11,a13,a33,a44,a66,θ0,φ0}的偏微分表达式,即速度敏感函数。利用弹性模量参数与Thomsen参数之间的关系式,可以进一步得到相速度对Thomsen参数的偏微分表达式。
2 速度敏感函数的数值模拟分析
利用数值模型对上述TTI介质速度敏感函数计算方法进行测试,通过数值模拟来分析VTI介质模型和TTI介质模型的速度敏感函数特性。图1 给出了测试采用的层间块状异常体模型,模型水平方向的长度为800m,深度为500m;模型的背景介质为VTI介质,其弹性模量参数为a11=12,a13=5,a33=10,a44=4,a66=6,对称轴倾角和方位角分别为θ0=0和φ0=0;模型内的块状异常体为TTI介质,其弹性模量参数为a11=20,a13=10,a33=15,a44=8,a66=12,对称轴倾角和方位角分别为θ0=450和φ0=0。

图1 层间块状异常体模型
2.1 VTI介质的速度敏感函数特性
首先分析模型背景VTI介质的速度敏感函数特性。图2到图4分别是VTI介质qP,qSV和qSH波的速度敏感函数,由这3张图可以看到,VTI介质中3种波的相速度对方位角φ的偏微分均等于0,这是因为VTI介质的相速度不随观测方位角的变化而变化。
图2是qP波的速度敏感函数图。从图2中可以看出∂c1/∂a11(图2a),∂c1/∂a33(图2c)和∂c1/∂a44(图2d)的峰值比∂c1/∂a13(图2b)的峰值大,这说明qP波的相速度对不同弹性参数的敏感性强度存在差别。另外,不同偏微分的峰值对应的观测角度也不一样,例如,∂c1/∂a11的峰值在90°附近,∂c1/∂a33的峰值在0和180°附近,∂c1/∂a13和∂c1/∂a44的峰值在45°和135°附近。∂c1/∂θ0(图2e)的数值从0到180°呈逐渐增大趋势。

图2 VTI介质qP波的相速度(c1)对弹性模量参数以及介质对称轴倾角和方位角的偏微分a c1对a11的偏微分; b c1对a13的偏微分; c c1对a33的偏微分; d c1对a44的偏微分; e c1对θ0的偏微分; f c1对φ0的偏微分
图3是qSV波的速度敏感函数图。与qP波的速度敏感函数特性类似,qSV波的相速度对不同弹性参数的敏感性强度也存在差别,不同偏微分的峰值出现在不同的观测角度范围内。
图4是qSH波的速度敏感函数图。qP波和qSV波的相速度与a11,a13,a33,a44,θ0,φ0有关,而qSH波的相速度与a44,a66,θ0,φ0有关。可以看出,∂c3/∂a44(图4a)和∂c3/∂a66(图4b)的敏感性强度大致相同,但是它们的敏感性峰值存在于不同的观测角度范围内,∂c3/∂a44的峰值在0和180°附近,∂c3/∂a66的峰值在90°附近。
从图2到图4可知,VTI介质不同弹性参数对应的速度敏感性强度存在差别,而且敏感性峰值对应的观测角度也不同。

图3 VTI介质qSV波的相速度(c2)对弹性模量参数以及介质对称轴倾角和方位角的偏微分a c2对a11的偏微分; b c2对a13的偏微分; c c2对a33的偏微分; d c2对a44的偏微分; e c2对θ0的偏微分; f c2对φ0的偏微分

图4 VTI介质qSH波的相速度(c3)对弹性模量参数以及介质对称轴倾角和方位角的偏微分a c3对a44的偏微分; b c3对a66的偏微分; c c3对θ0的偏微分; d c3对φ0的偏微分
2.2 TTI介质的速度敏感函数特性
继续分析模型中异常体TTI介质的速度敏感函数特性。图5到图9分别是qP波、qSV波和qSH波的速度敏感函数。由图5到图9可以看到,TTI介质的速度敏感函数比VTI介质的速度敏感函数复杂得多,这是因为岩石的对称轴倾角θ0和方位角φ0,任何一个发生变化都会使速度敏感函数产生变化。TTI介质的速度敏感函数粗看起来似乎没有规律,实际上仍然可以看出各个弹性参数对应的速度敏感函数强度大小,以及速度敏感函数峰值的分布区间。例如,qP波的速度敏感函数(图5,图6),∂c1/∂a13比其它5个参数的敏感性峰值更小,∂c1/∂a11的敏感性相对还较简单,其它5个参数的敏感性变化更加剧烈。

图5 TTI介质qP波的相速度(c1)对介质对称轴倾角θ0(a)和方位角φ0(b)的偏微分

图6 TTI介质qP波的相速度(c1)对弹性模量参数的偏微分a c1对a11的偏微分; b c1对a13的偏微分; c c1对a33的偏微分; d c1对a44的偏微分

图7 TTI介质qSV波的相速度(c2)对弹性模量参数的偏微分a c2对a11的偏微分; b c2对a13的偏微分; c c2对a33的偏微分; d c2对a44的偏微分
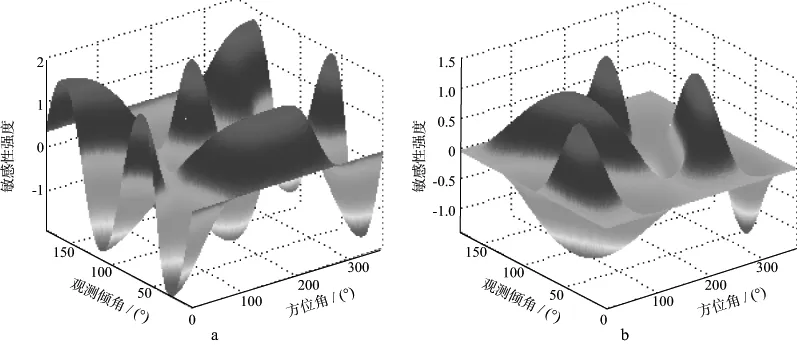
图8 TTI介质qSV波的相速度(c2)对介质对称轴倾角θ0(a)和方位角φ0(b)的偏微分

图9 TTI介质qSH波的相速度(c3)对弹性模量参数以及介质对称轴倾角和方位角的偏微分a c3对a44的偏微分; b c3对a66的偏微分; c c3对θ0的偏微分; d c3对φ0的偏微分
3 速度敏感函数计算方法验证
为了验证本文推导出的速度敏感函数计算方法的正确性,编写了TI介质反射波非线性走时反演算法程序,利用该算法对层间块状异常体模型进行qP波走时反演,同时结合速度敏感函数分析弹性参数反演结果。根据反演理论,多参数反演会发生耦合效应,这样会导致反演结果的不确定性增强,所以这里只对5个弹性参数进行反演。将背景介质作为反演的初始模型,块状异常体作为反演目标。在模型上表面(地表)进行激发和接收,道间距为16m,炮点与检波点均为51个。模型的网格间距为50m,对于5个弹性参数剖面,需要求解的未知量一共有935个,而反射波走时有2601个,反问题处于超定形式。图10为层间块状异常体模型正演的射线路径分布图。

图10 层间块状异常体模型正演射线路径分布
图11为块状异常体的速度敏感函数图(图中紫线代表∂c1/∂a11;红线代表∂c1/∂a13;绿线代表∂c1/∂a33;蓝线代表∂c1/∂a44)。由图11可以看出,a11的速度敏感函数(紫色曲线)的敏感性最弱,由此预测较难得到正确的反演结果;a33的速度敏感函数(绿色曲线)在射线照射角度为45°和135°附近时最强,由于地表观测方式在45°和135°附近的射线较多,可以预测能够比较容易地得到正确的反演结果;a13和a44的速度敏感函数(红色和蓝色曲线)形态相似,但是a44比a13的敏感性强,在射线照射角度为0,90°和180°附近时较为敏感,由于水平与垂直方向的射线较少,所以它们的反演难度较a33困难。因此,预测4个弹性参数的敏感性强度排序为a33>a44>a13>a11。

图11 块状异常体的速度敏感函数曲线
图12为真实弹性参数剖面与反演剖面的对比图,左侧为真实剖面,右侧为反演剖面。由于很难反演得到a11参数的正确结果,这里只给出了a13,a33和a44的反演剖面。由图12可以看出,a33的反演效果最好,a13和a44的反演效果相当,反演结果与速度敏感函数的预测结果一致。由此验证了TI介质速度敏感函数计算方法的正确性,也证实了速度敏感函数对反演结果具有预测和指示作用。

图12 层间块状异常体模型弹性参数(a13,a33,a44)的真实剖面(a)与反演剖面(b)
4 结束语
速度敏感函数有群速度偏微分和相速度偏微分两种,由于群速度是相速度的函数,所以相速度偏微分表达速度敏感函数更加简便。我们基于TTI介质模型推导出了相速度偏微分形式的速度敏感函数计算方法,并对层间块状异常体模型的背景VTI介质和块状TTI介质异常体分别模拟计算了速度敏感函数。对速度敏感函数特性进行分析得出5点结论:①同一种波模式,不同弹性参数的速度敏感性强度不同;②速度敏感函数在不同观测角度的敏感性强度不同;③VTI介质的速度敏感函数在观测倾角为0~90°和90°~180°呈对称关系;④VTI介质的速度敏感函数不随观测方位角发生变化;⑤TTI介质的速度敏感函数比VTI介质复杂得多,它的敏感性随观测角度的变化而变化。
由于速度敏感函数是各向异性介质走时扰动方程的重要组成成分,文中利用TI介质反射波非线性走时反演算法对层间块状异常体模型进行反演,得到了a13,a33和a44参数的反演结果,从而验证了本文速度敏感函数计算方法的正确性,也证实了速度敏感函数对反演结果具有预测和指示作用。
致谢:感谢澳大利亚阿德莱德大学周兵高级研究员对本文给予的指导和帮助。
参 考 文 献
[1] Crampin S.Effective anisotropic elastic constants for wave-propagation through cracked solids[J].Geophysical Journal of the Royal Astronomical Society,1984,76:135-145
[2] Helbig K.Systematic classification of layered-induced transverse isotropy[J].Geophysical Prospecting,1981,29:550-577
[3] Thomsen L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954-1966
[4] 李芳,曹思远,姚健.任意各向异性介质相(群)速度的计算[J].地球物理学报,2012,55(10):3420-3426
Li F,Cao S Y,Yao J.Calculation of phase and group velocities in an arbitrary anisotropic medium[J].Chinese Journal of Geophysics,2012,55(10):3420-3426
[5] Every A G,Sachse W.Sensitivity of inversion algorithms for recovering elastic constants of anisotropic solids from longitudinal wavespeed data[J].Ultrasonics,1992,30(4):43-48
[6] Chapman C H,Miller D E.Velocity sensitivity in transversely isotropic media[J].Geophysical Prospecting,1996,44:525-549
[7] Zhou B,Greenhalgh S A.Analytic expressions for the velocity sensitivity to the elastic moduli for the most general anisotropic media[J].Geophysical Prospecting,2005,53:619-641
[8] Cerveny V,Jech J.Linearized solutions of kinematic problems of seismic body waves in inhomogeneous slightly anisotropic media[J].Journal of Geophysics,1982,51:96-104
[9] Jech J,Psencik I.First-order perturbation method for anisotropic media[J].Geophysical Journal International,1989,99:369-376
[10] Chapman C H,Pratt R G.Traveltime tomography in anisotropic media-I[J].Geophysical Journal International,1992,109:1-19
[11] Pratt R G,Chapman C H.Traveltime tomography in anisotropic media-II[J].Geophysical Journal International,1992,109:20-37
[12] Zhou B,Greenhalgh S A.Non-linear traveltime inversion for 3-D seismic tomography in strongly anisotropic media[J].Geophysical Journal International,2008,172:383-394
[13] Zhou B,Greenhalgh S A.Raypath and traveltime computations for 2D transversely isotropic media with dipping symmetry axes[J].Exploration Geophysics,2006,37(2):150-159

