Numerical Solution of Fractional Fredholm-Volterra Integro-Differential Equations by Means of Generalized Hat Functions Method
Baofeng Li
1 Introduction
Fractional calculus has been known for more than 300 years.These fractional phenomena allow us to describe a real object more accurately than the classical integer order methods.As we all know,the nature of real objects is fractional.However,for many of them the fractionality is very low.The fractional system describes many typical examples,such us the voltage current relation of a semi-infinite lossy transmission line[Wang(1987)],the diffusion of heat through a semi-infinite solid,where heat flow is equal to the half derivative of the temperature[Westerlund(2002)].In recent years,there are a lot of methods for approximation of fractional derivatives and integrals can be used in wide filed of applications.Fractional order calculus plays an important roles in electrical engineering[Nakagava and Sorimachi(1992)],physics[Valdes-Parada;Ochoa-Tapia;Alvarez-Ramirez(2007)],signal processing[Vinagre and Chen(2003);Tseng(2007)],robotics[Maria da Graca Marcos,Duarte,Tenreiro Machado(2008)],chemistry[Oldham and Spanier(1974)],chaos[Tavazoei and Haeri(2008)],and so on.In general,it is difficult to derive the analytical solutions to most of the fractional differential equations.Therefore,it is important to develop some reliable and efficient techniques to solve fractional differential equations[Chen,Yi,Chen and Yu(2012);Yi and Chen(2012);Chen,Sun,Li and Fu(2013)].The numerical solutions of fractional differential equations have attracted considerable attention from many researchers.The most commonly used methods are Variational Iteration Method[Zaid M.Odibat(2010)],Adomian Decomposition Method[EI-Kalla(2008)and Hosseini(2006)],and Generalized Differential Transform Method[Shaher and Zaid(2007);Zaid and Shaher(2008)].Wavelet basis approach has also been successfully employed to solve the factional differential equations.
The motivation of this paper is to extend the application of generalized hat functions to provide approximate solution of linear and nonlinear integro-differential equations of fractional order.The linear and nonlinear integro-differential equations of fractional order can be solved by many numerical methods.Saeedi and Moghadam[Saeedi and Moghadam(2011)]applied CAS wavelets method to solve the numerical solution of nonlinear Volterra integro-differential equations of fractional order and nonlinear Fredholm integro-differential equations of fractional order.In Refs.[Zhu and Fan(2013),Zhu and Fan(2012)],the authors solved the same integrodifferential equations by using the second kind Chebyshev wavelets[Babolian and Mordad(2011)].
The structure of this paper is as follows:In Section 2,the generalized hat functions are introduced.The generalized hat functions operational matrix of fractional integration is also introduced and the error analysis of generalized hat functions is given in Section 3.In Section 4,we summarize the application of generalized hat functions operational matrix method to the solution of the fractional integro-differential equation.Four numerical examples are provided to clarify the approach in Section 5.The conclusion is given in Section 6.
2 Generalized hat functions and their properties

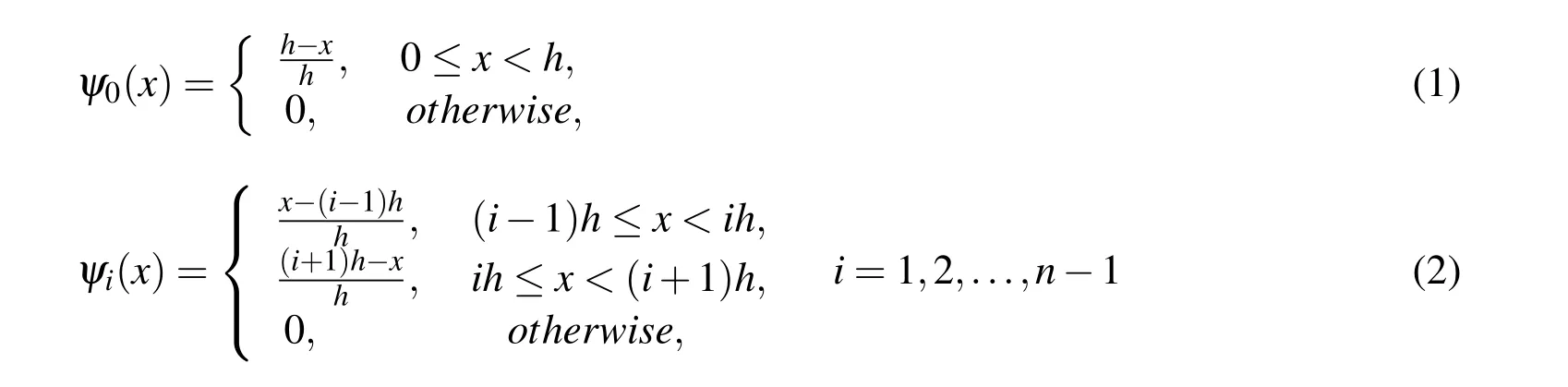
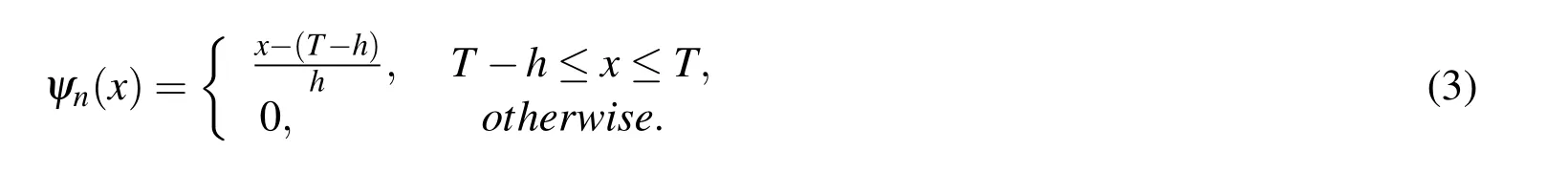
Using the definition of generalized hat functions,we can obtain

An arbitrary functionu∈L2[0,T]is approximated in vector form as

whereUn+1=[u0,u1,...,un]Tand Ψn+1(x)=[ψ0(x),ψ1(x),...,ψn(x)]T.
Substituting Eq.(1)-(3)into the Eq.(6),we get the coefficients in Eq.(6)as following

3 Operational matrix of the integration for generalized hat functions
3.1 Fractional calculus
Before we introduce the generalized hat functions operational matrix of the fractional integration,we first review some basic definitions of fractional calculus,which have been given in[Li and Sun(2011)].
Definition 1.The Riemann-Liouville fractional integral of orderαis given by
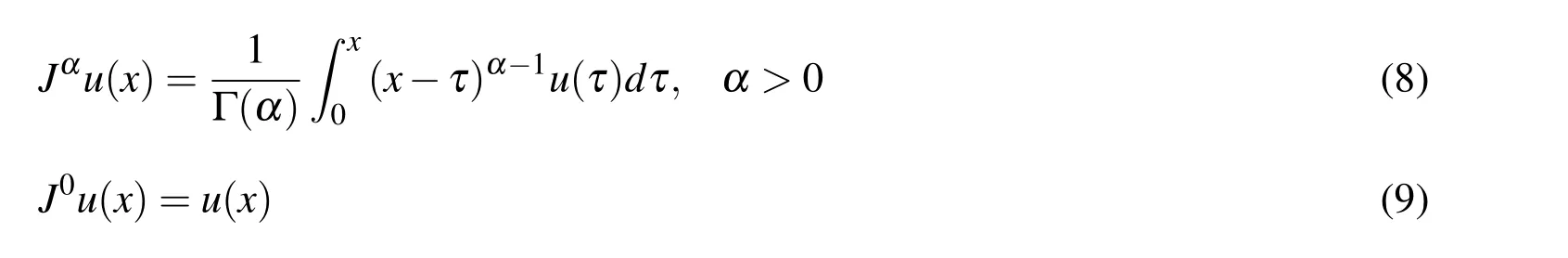
Definition 2.The Caputo definition of fractional differential operator is given by
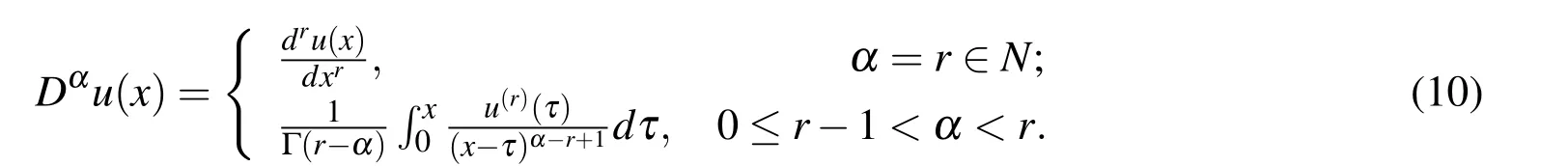
The Caputo fractional derivatives of orderαis also defined asDαu(x)=Jr−αDru(x),whereDris the usual integer differential operator of orderr.The relation between the Riemann-Liouville operator and Caputo operator is given by the following expressions:
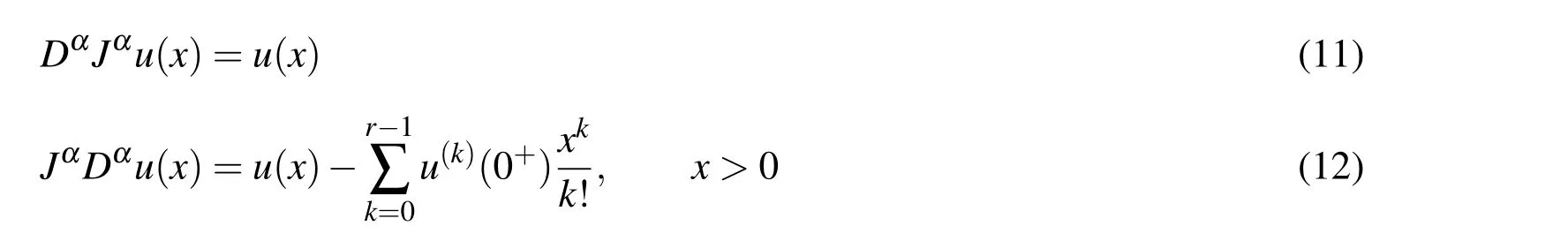
3.2 Fractional order generalized hat functions operational matrix of integration.
IfJαis fractional integration operator of generalized hat functions,we can get:

Apart from the generalized hat functions,we consider another basis set of block pulse functions.The set of these functions,over the interval[0,T),is defined as


LetBn(x)=[b0(x),b1(x),...,bn−1(x)]T.SupposeJα(Bn(x))≈FαnBn(x),thenFαnis called the block pulse operational matrix of fractional integration[21],here
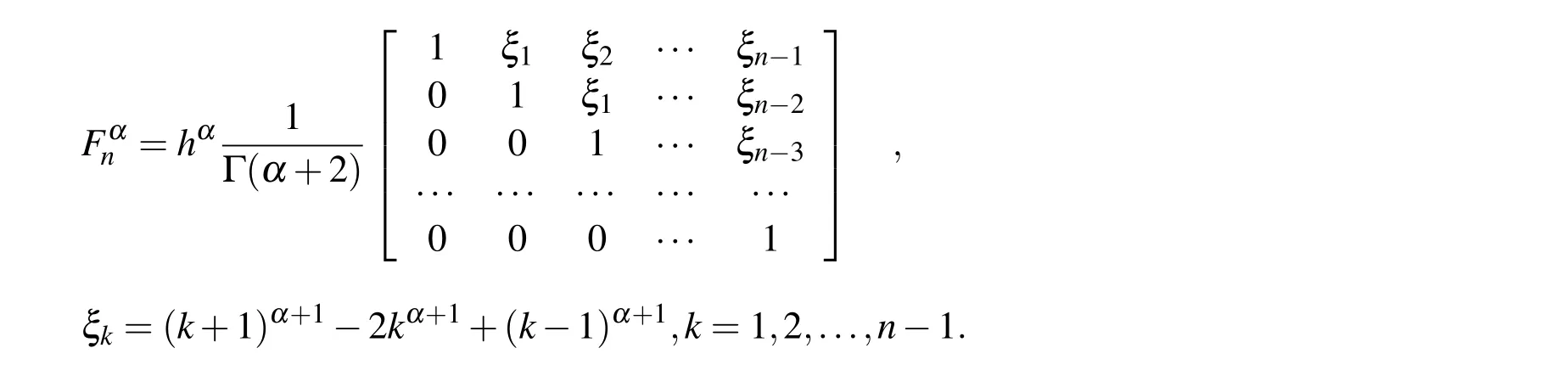
There is a relation between the block pulse functions and generalized hat functions,namely
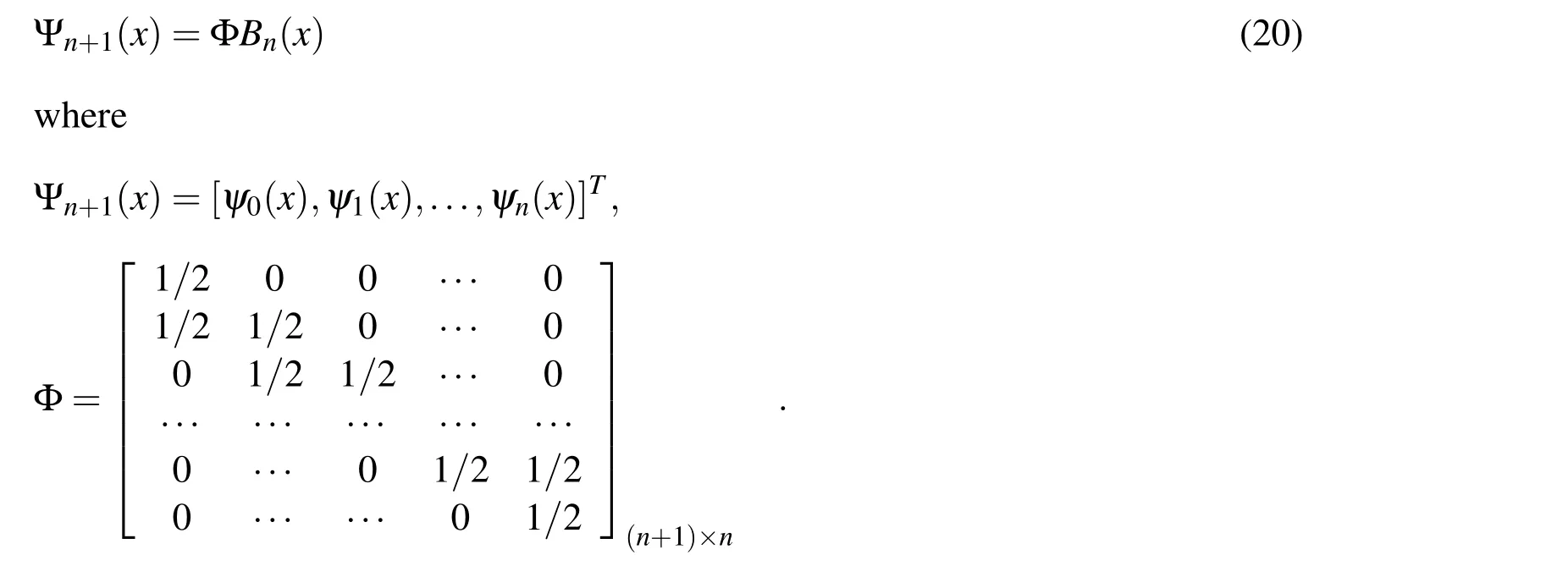
3.3 Error analysis
In this section,from Eq.(6),we suppose
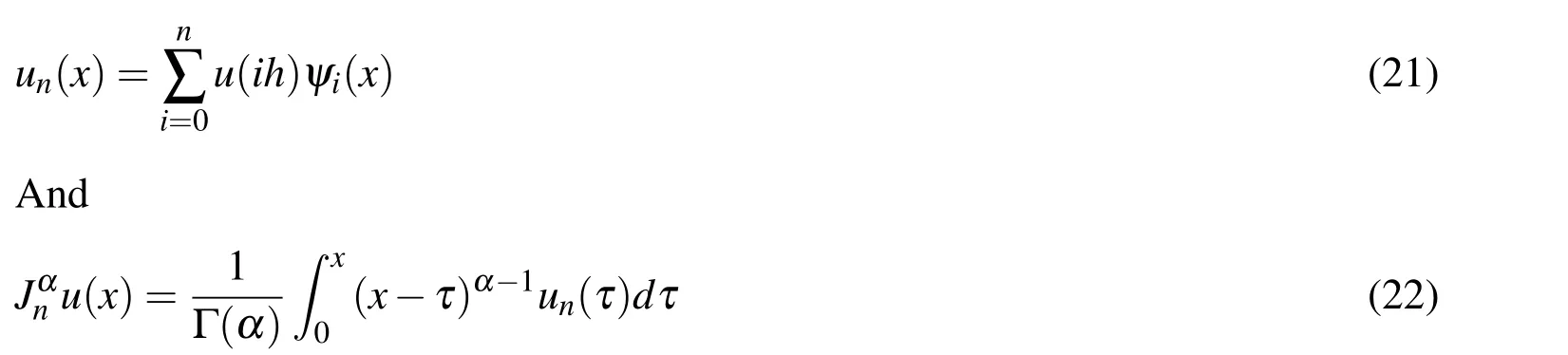
whereJαnu(x)denotes the approximation ofαorder Riemann-Liouville fractional integral ofu(x).Letεn(x)=|Jαu(x)−Jαnu(x)|,then we have the following theorem.
Theorem 3.1Ifu(x),x∈[0,T]is approximated by the Eq.(6),then
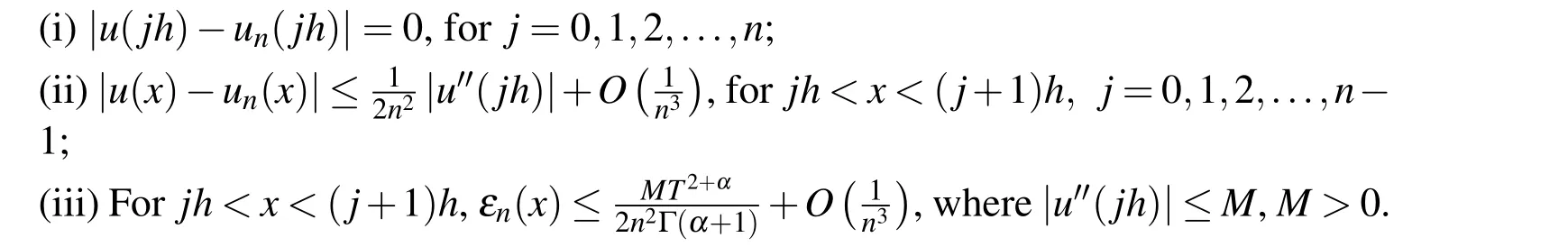
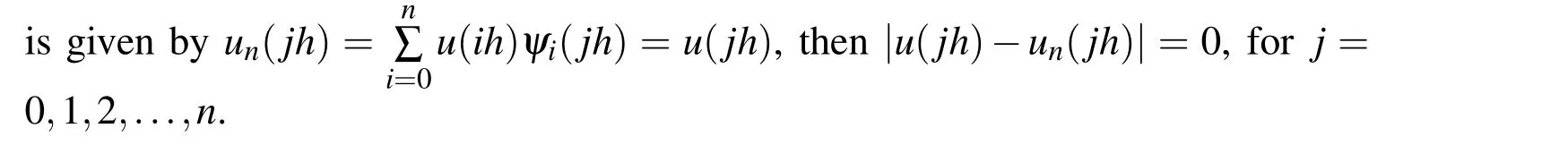
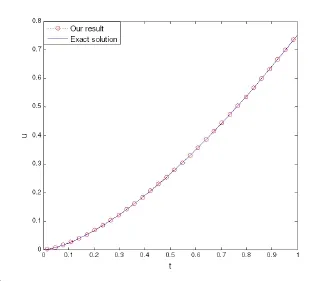
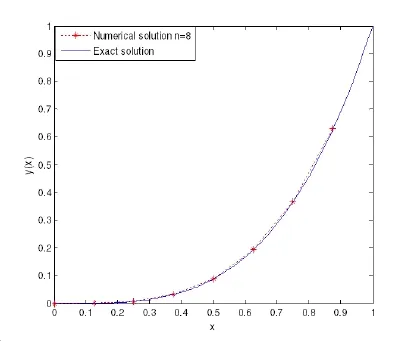
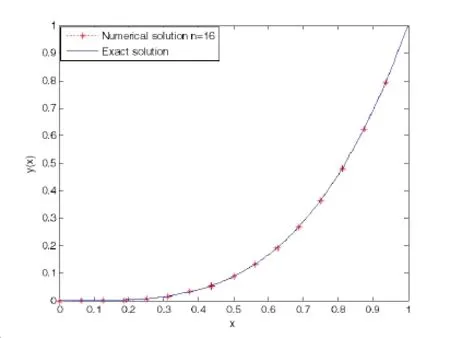
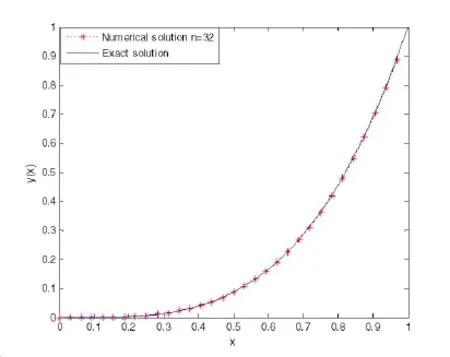
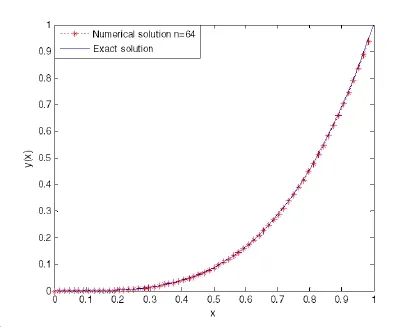
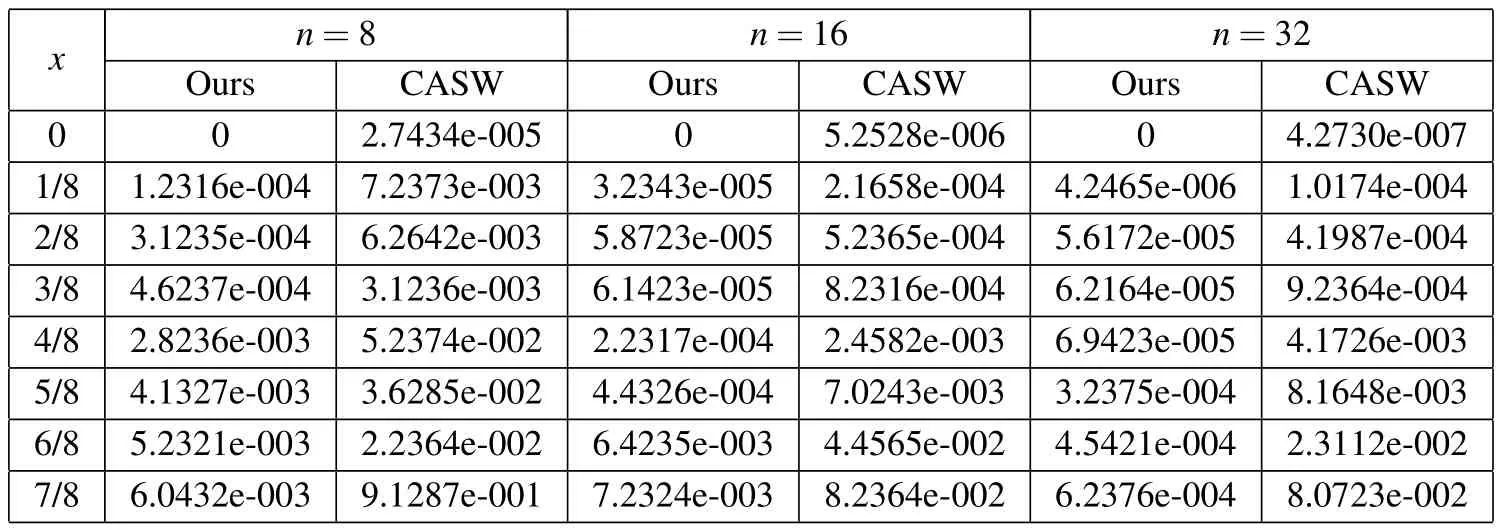
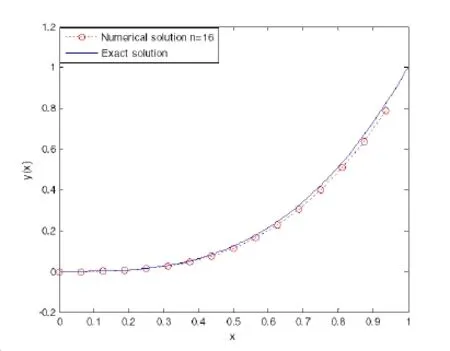
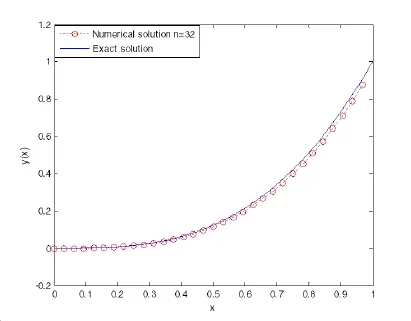
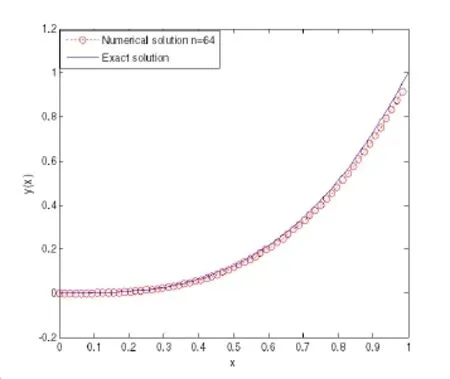
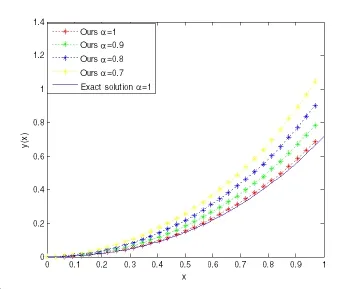
(ii)Ifjh Using the Taylor’s series ofu(x),in the powers of(x−jh),we have whereu(k)denotes thekth order derivative ofu(x).From Eq.(24)and Eq.(25),we get 2.1 两组患者临床疗效比较 观察组患者治愈率高于对照组,组间比较差异有统计学意义(χ2=8.362,P<0.05),见表1。 (iii)According to the definition of the absolute errorεn(x),we obtain Forjh Substituting Eq.(27)into Eq.(29),we have IfMax|u00(kh)|≤M,k=0,1,2,...,j,then we obtain This completes the proof. Whenα=0.5,m=32,the comparison results for the fractional integration is shown in Figure 1 Consider the linear fractional integro-differential equations subject to initial conditions Figure 1:0.5-order integration of the function u(t)=t. whereu(s)(x)stands for thesth-order derivative ofu(x),Dα(·)denotes the Caputo fractional order derivative of orderα,f(x)is input term andu(x)is the output response.k1(x,t),k2(x,t)are given functions.λ1,λ2are real constants. Now we approximateDαu(x),k1(x,t),k2(x,t)andf(x)in terms of generalized hat functions as follows Now using Eq.(35)and Eq.(12),we obtain Substituting Eq.(20)into Eq.(37),we have Substituting the above equations into Eq.(33),we have which is a linear system of algebraic equations.By solving this system we can obtain the approximation of Eq.(37). In this section we deal with nonlinear fractional integro-differential equation of the form subject to initial conditions wherep,q∈N,and the other parameters and variables are the same as the section 4.1.While dealing with such a situation,the same procedure(as in linear case)of expansion of fractional order derivatives via generalized hat functions is adopted with exception at the term containing[u(t)]p,[u(t)]q. From Eq.(38),we haveu(x)≈EBn(x)and hence Following the procedure of section 4.1 and using the Eq.(45)and Eq.(46),the Eq.(44)is transformed into a nonlinear system of algebraic equations Solving the system of equations given by Eq.(47),the approximate numerical solutionu(x)is obtained.The Eq.(47)can be solved by iterative numerical technique such as Newton’s method.Also the Matlab function “fsolve”is available to deal with such a nonlinear system of algebraic equations. In order to illustrate the effectiveness of the proposed method,we consider numerical examples of linear and nonlinear nature. Example 5.1Consider this equation: Figure 2:Comparison of Num.sol.and Exa.Sol.of n=8. Example 5.2Consider the following nonlinear equation: Figure 3:Comparison of Num.sol.and Exa.Sol.of n=16. Figure 4:Comparison of Num.sol.and Exa.Sol.of n=32. Figure 5:Comparison of Num.sol.and Exa.Sol.of n=64. Table 1:The absolute errors for different values of n. We can see that the numerical solutions are more and more close to the exact solution with the value ofnbecomes large by taking a closer look at Figures 6-8. Example 5.3Consider this equation: Figure 6:Comparison of Num.sol.and Exa.Sol.of n=16 for Example 3. Figure 7:Comparison of Num.sol.and Exa.Sol.of n=32for Example 3. The comparison of numerical results forα=0.7,α=0.8,α=0.9,α=1 and the exact solution forα=1 are shown in Figure.9. Figure 8:Comparison of Num.sol.and Exa.Sol.of n=64for Example 3. Figure 9:Numerical solution and exact solution of α=1. From Figure 9,we can see clearly that the numerical solutions are in very good agreement with the exact solution whenα=1.It is evident from the Figure 9 that,asαclose to 1,the numerical solutions by the generalized hat functions converge to the exact solution. In this work,we introduce the generalized hat functions and operational matrix of the fractional integration.Using the operational matrix to solve the fractional linear and nonlinear integro-differential equations numerically.By solving the linear and nonlinear system,numerical solutions are obtained.The error analysis of generalized hat functions is proposed.The numerical results show that the approximations are in very good coincidence with the exact solution Acknowledgement:This work is supported by the Natural Science Foundation of Tangshan Normal University(2014D09). Babolian,E.;Mordad,M.(2011):A numerical method for solving systems of linear and nonlinear integral equations of second kind by hat basis functions.Comput.Math.Appl,vol.62,no.1,pp.187-198. Chen,Y.M.;Yi,M.X.;Chen,C.;Yu,C.X.(2012):Bernstein polynomials method for fractional convection-diffusion equation with variable coefficients.Computer Modeling in Engineering&Sciences,vol.83,no.6,pp.639-653. Chen,Y.M.;Sun,L.;Li,X.;Fu,X.H.(2013):Numerical solution of nonlinear fractional integral differential equations by using the second kind Chebyshev wavelets.Computer Modeling in Engineering&Sciences,vol.90,no.5,pp.359-378. da Graca Marcos,M.;Duarte,F.;Tenreiro Machado,J.A.(2008):Fractional dynamics in the trajectory control of redundant manipulators.Communications in Nonlinear Science and Numerical Simulations,vol.13,pp.1836-1844. EI-Kalla,I.L.(2008):Convergence of the Adomian method applied to a class of nonlinear integral equations.Applied Mathematics and Computation,vol.21,pp.372-376. Hosseini,M.M.(2006):Adomian decomposition method for solution of nonlinear differential algebraic equations.Applied Mathematics and Computation,vol,181,pp.1737-1744. Li,Y.L.;Sun,N.(2011):Numerical solution of fractional differential equations using the generalized block pulse operational matrix.Comput.Math.Appl,vol.62,pp.1046-1054. Momani,S.;Odibat,Z.(2007):Generalized differential transform method for solving a space and time-fractional diffusion-wave equation.Physics Letters A,vol.370,pp.379-387. Nakagava,M.;Sorimachi,K.(1992):Basic characteristics of a fractance device,IEICE Transactions on Fundamentals of Electronics.Communications and Computer Sciences,vol.E75-A,no.12,pp.1814-1818. Oldham,K.B.;Spanier,J.(1974):The Fractional Calculus,Academic Press,New York. Odibat,Z.M.(2010):A study on the convergence of variational iteration method.Mathematical and Computer Modelling,vol.51,pp.1181-1192. Odibat,Z.;Momani,S.(2008):Generalized differential transform method:Application to differential equations of fractional order.Applied Mathematics and Computation,vol.197,pp.467-477. Podlubny,I.(1999):Fractional Differential Equations,Academic press. Saeedi,H.;Moghadam,M.M.(2011):Numerical solution of nonlinear Volterra integro-differential equations of arbitrary order by CAS wavelets.Commun.Nonlinear Sci.Numer.Simulat.,vol.16,pp.1216-1226. Saeedi,H.;Moghadam,M.M.;Mollahasani,N.;Chuev,G.N.(2011):A CAS wavelet method for solving nonlinear Fredholm integro-differential equations of fractional order.Commun.Nonlinear Sci.Numer.Simulat,vol.16,pp.1154-1163. Tseng,Ch.(2007):Design of FIR and IIR fractional order Simpson digital integrators.Signal Processing,vol.87,pp.1045-1057. Tavazoei,M.S.;Haeri,M.(2008):Chaotic attractors in incommensurate fractional order systems.Physical D,vol.237,pp.2628-2637. Valdes-Parada,F.J.;Ochoa-Tapia,J.A.;Alvarez-Ramirez,J.(2007):Effective medium equations for fractional Fick’s law in porous media.Physical A,vol.373,pp.339-353. Vinagre,B.M.;Chen,Y.Q.(2003):Two direct Tustin discretization methods for fractional-order differentiator/integrator.Journal of the Franklin Institute,vol.340,pp.349-362. Wang,J.C.(1987):Realizations of generalized Warburg impedance with RC ladder networks and transmission lines.Journal of the Electrochemical Society,vol.134,no.8,pp.1915-1920. Westerlund,S.(2002):Dead Matter Has Memory,Causal Consulting,Kalmar,Sweden,2002. Yi,M.X.;Chen,Y.M.(2012):Haar wavelet operational matrix method for solving fractional partial differential equations.Computer Modeling in Engineering&Sciences,vol.88,no.3,pp.229-244. Zhu,L.;Fan,Q.B.(2013):Numerical solution of nonlinear fractional-order Volterra integro-differential equations by SCW,Commun.Nonlinear Sci.Numer.Simulat.,vol.18,pp.1203-1213. Zhu,L.;Fan,Q.B.(2012):Solving fractional nonlinear Fredholm integro-differential equations by the second kind Chebyshev wavelet.Commun.Nonlinear Sci.Numer.Simulat.,vol.17,pp.2333-2341.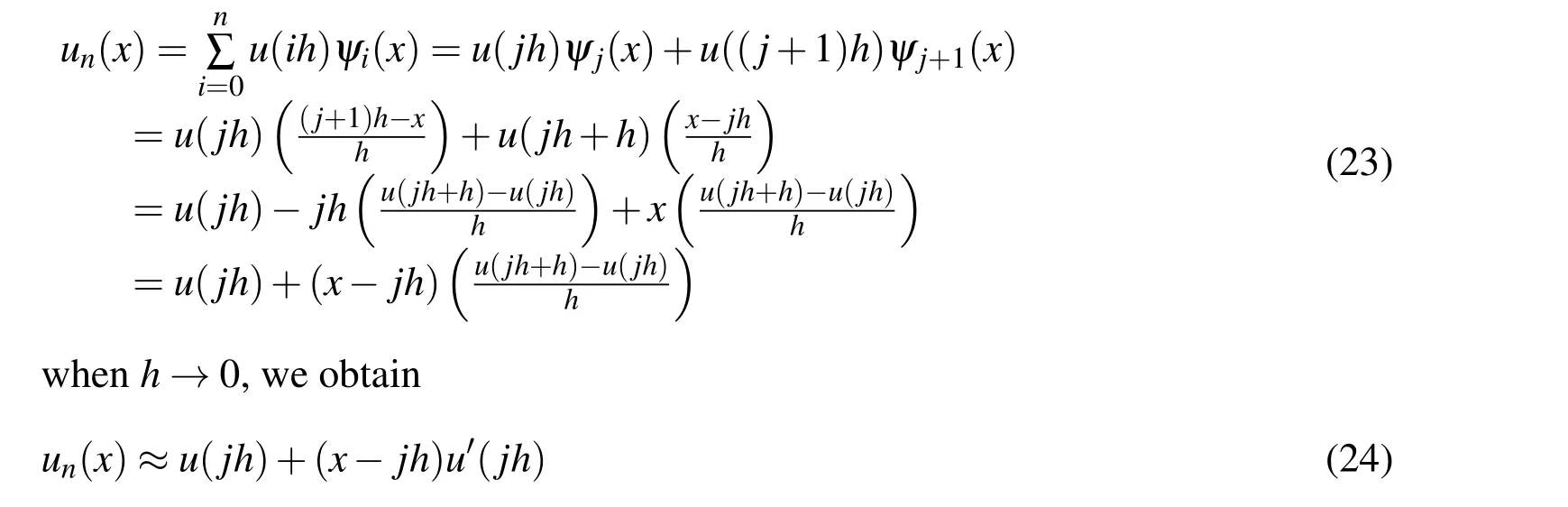

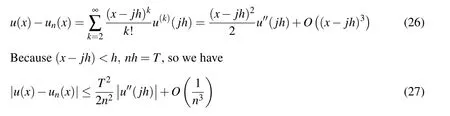
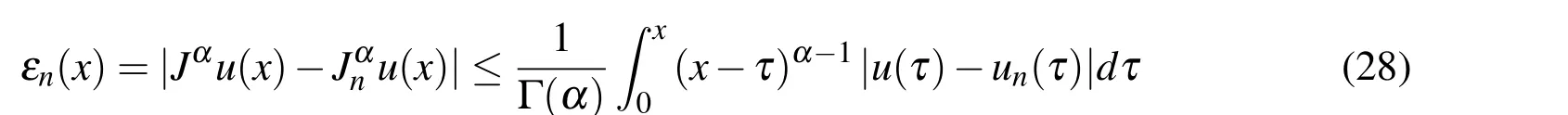
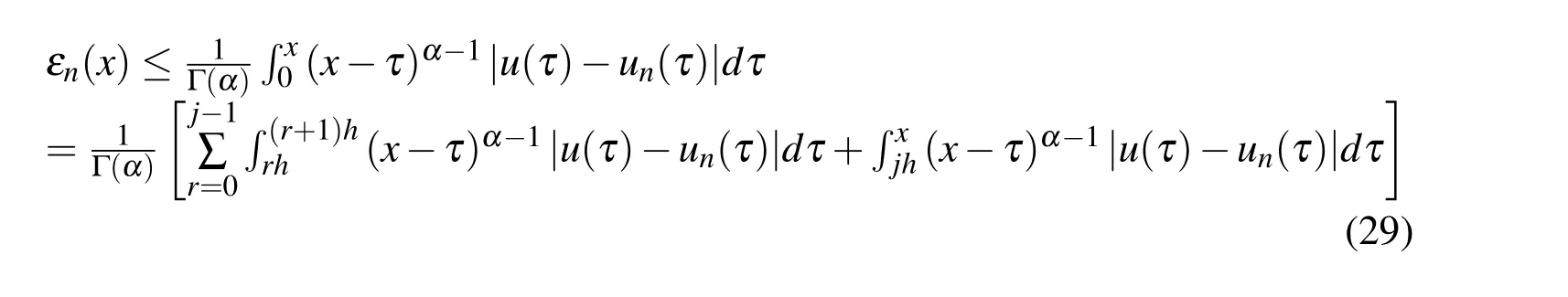
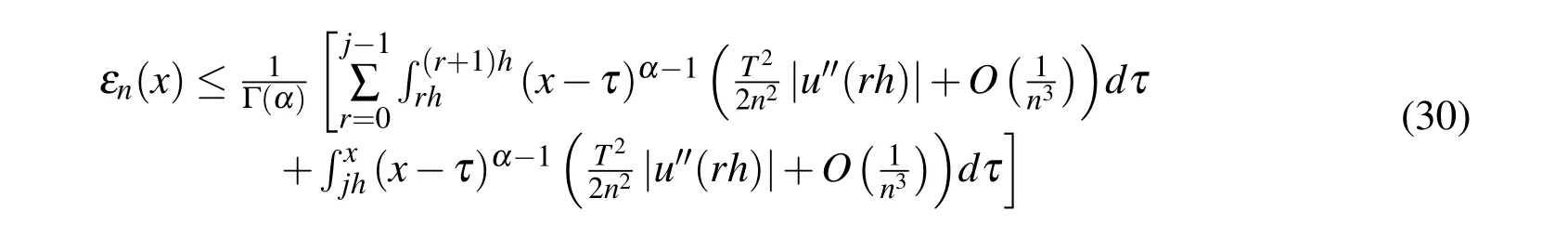
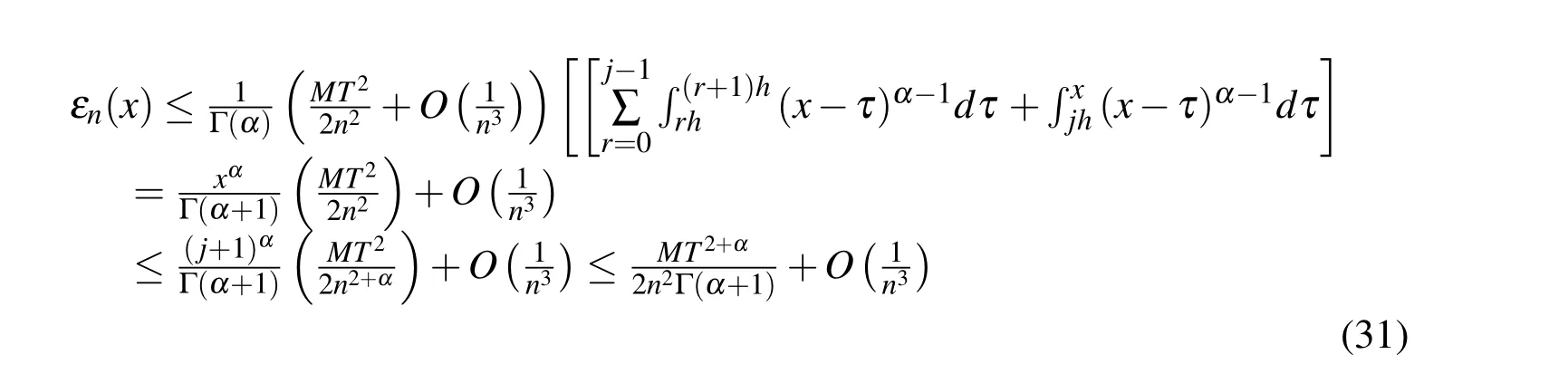
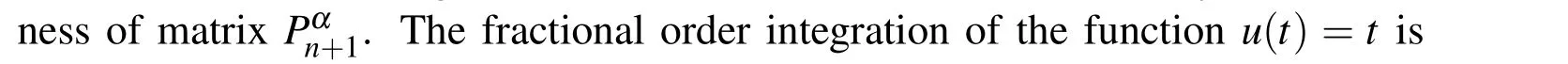

4 The algorithm for finding numerical solution of fractional integro-differential equations
4.1 Linear fractional integro-differential equations
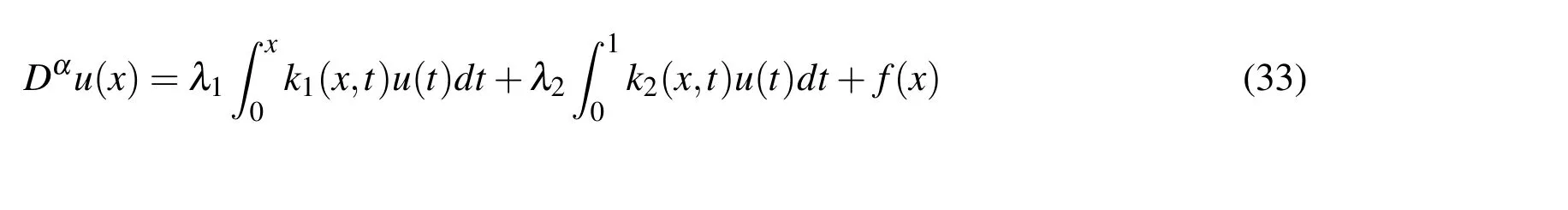

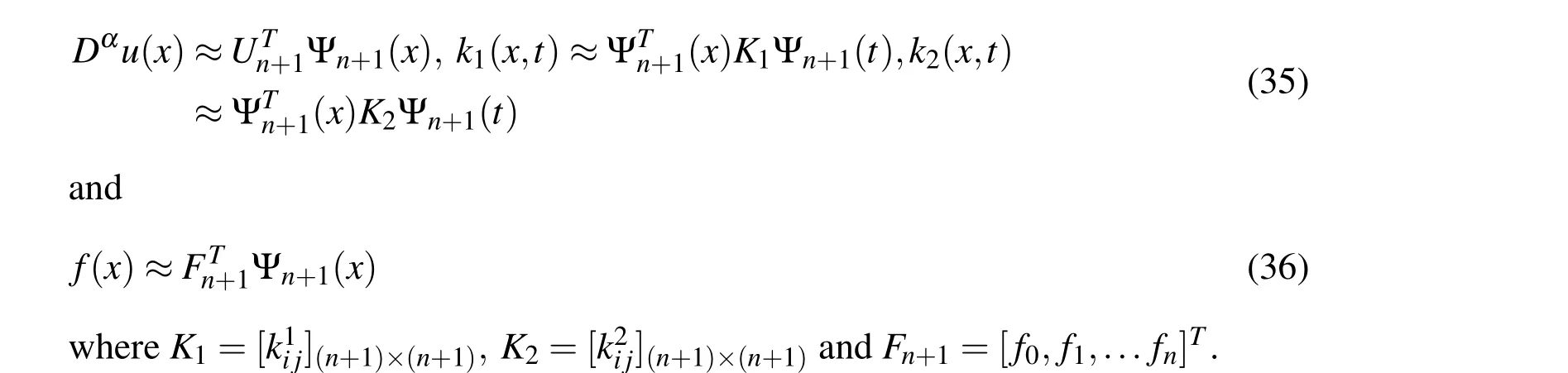
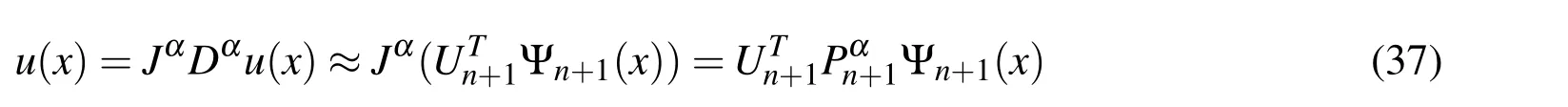

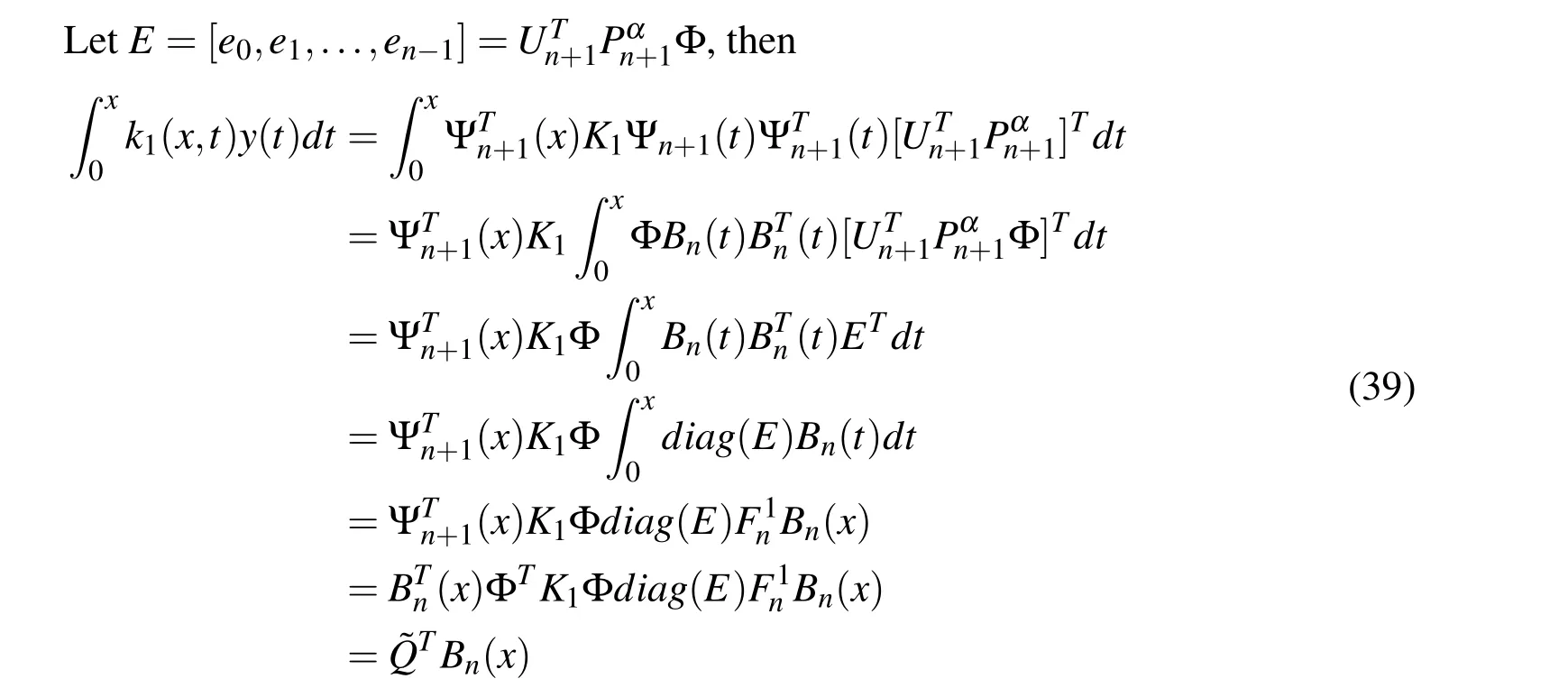
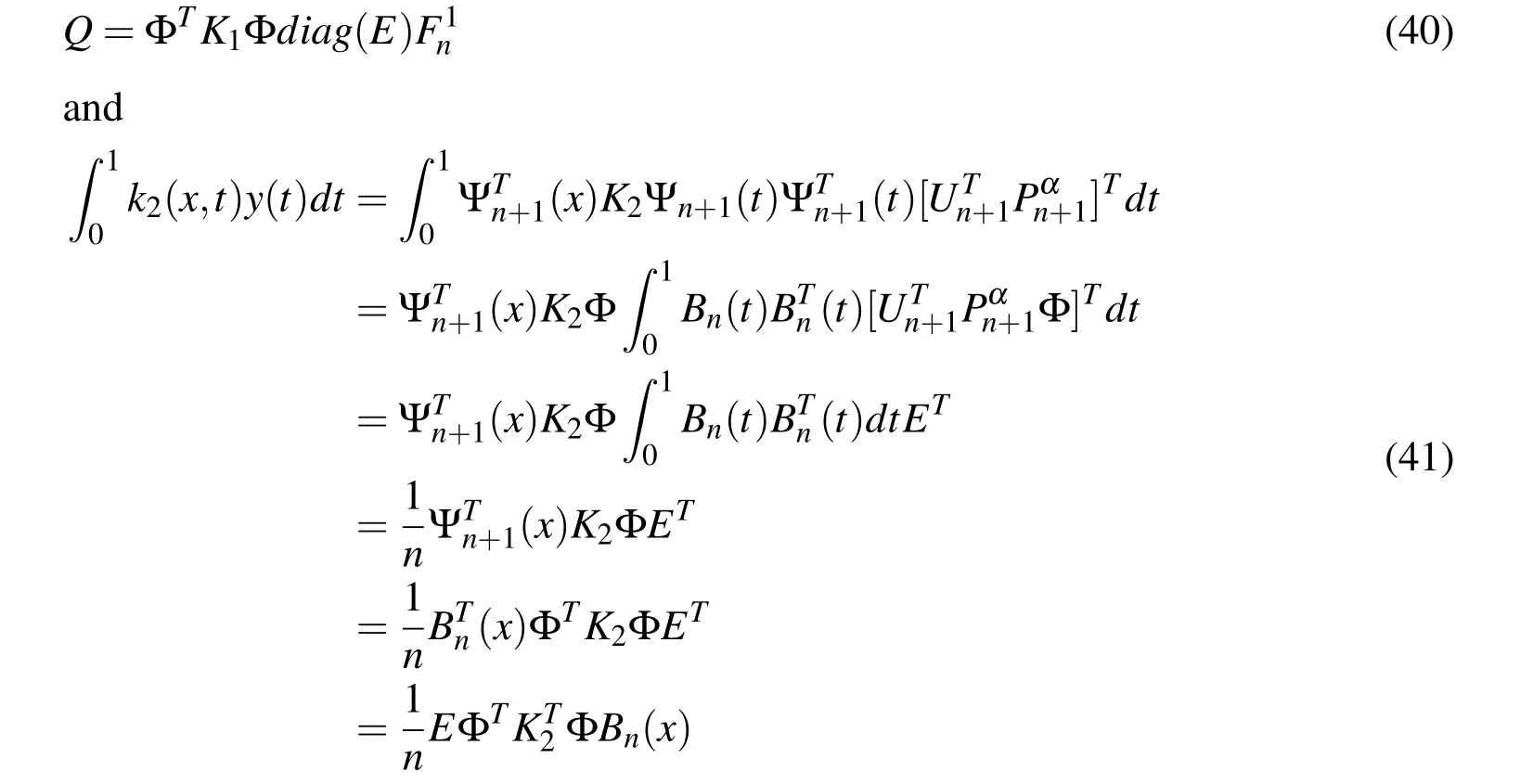
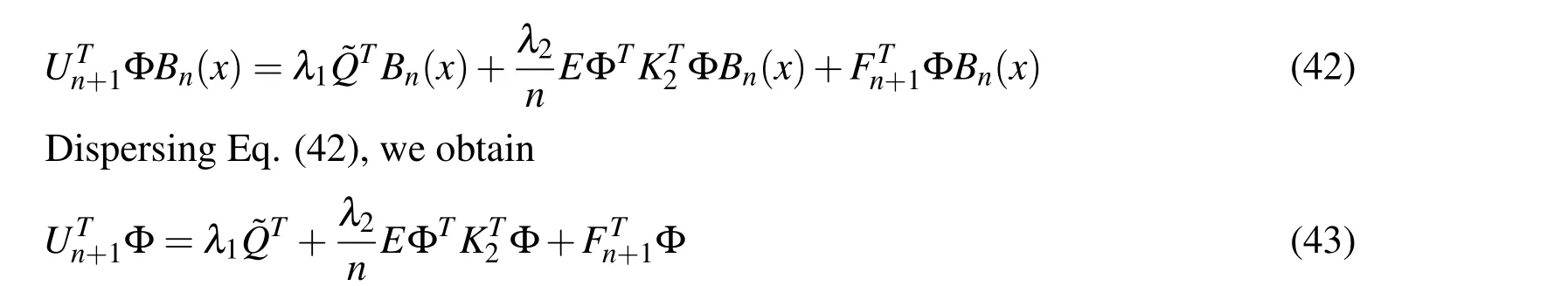
4.2 Nonlinear fractional integro-differential equations
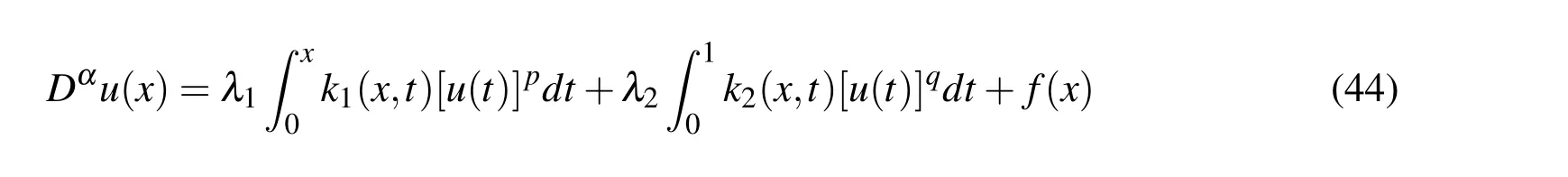

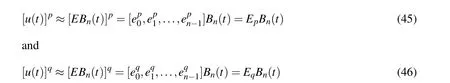
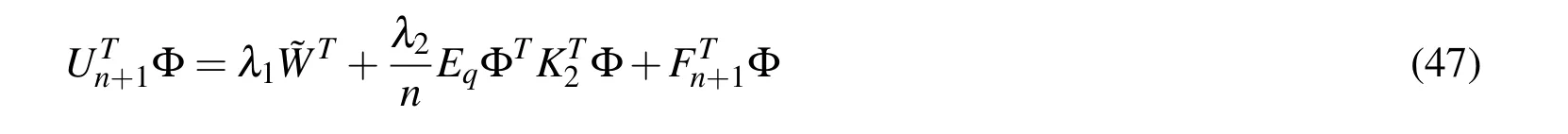

5 Numerical examples
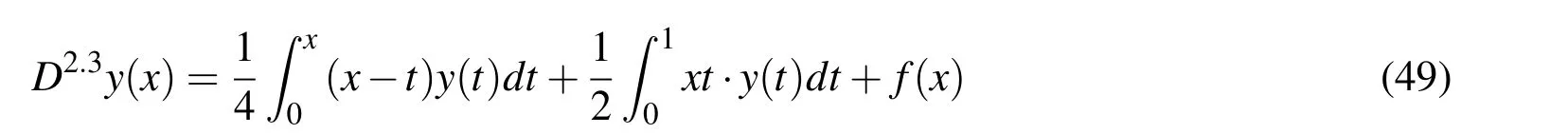

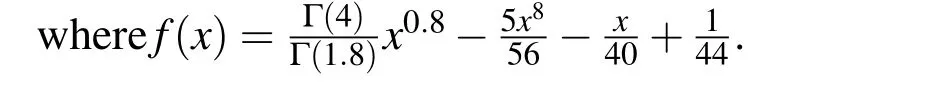
6 Conclusion
 Computer Modeling In Engineering&Sciences2014年14期
Computer Modeling In Engineering&Sciences2014年14期
