Simulation of Stress Concentration Problem s by Hexahedral Hybrid-Trefftz Finite Element M odels

F.L.S.Bussamra,E.Lucena Neto and W.M.Ponciano

1　Introduction

The displacement-based finite element models are traditionally the most currently used in structural analysis because of their simplicity and general effectiveness.However,there are certain analyses in which these models are not sufficiently effective.As an example,the stress field provided by them is likely to display greater error than the displacement field.The reason for this behavior is that the stress field is obtained by differentiation of the displacement field,and differentiation discloses differences.Computed stresses are usually most accurate at locations within an element rather than on its boundaries.This is unfortunate because stresses of greatest interest usually appear at boundaries.Therefore,stresses may be calculated at certain points within an element,then extrapolated to element boundaries,or treated by some smoothing scheme.Stress smoothing is discussed by[Hinton and Campbell(1974)];Hinton,Scott and Ricketts(1975)].The lower quality of the predicted stress field becomes yet worse in the presence of sharp geometric discontinuities caused by cracks,holes, fillets and notches,where stresses are the most relevant mechanical quantities[Cook,Malkus,Plesha and Witt(2002);Bathe(1996)].

Mixed,hybrid and mixed-hybrid formulations have been developed to offer some advantages compared to the standard displacement-based formulation.A hybrid stress finite element formulation,for instance,is based on the independent approximation of stresses within the element and displacements on its boundary.As displacements are not favor over stresses or vice versa,a better stress description perm its the improvement of the stress approximation[Kardestuncer(1988)].

Trefftz elements,a kind of hybrid elements,are known to produce accurate stress estimates.The strongest limitation in developing this type of element is the fulfillment of the Trefftz constraint,i.e.,the stress bases must be extracted from the Navier equation solution of the problem being analyzed.The derivation of such bases may not be trivial.However,once these bases are secured,the advantages offered by Trefftz elements are difficult to surpass as they combine the major features of the competing finite element and boundary element methods[Freitas and Cismasiu(2001)].

Many authors have proposed the enrichment of the original approximation functions set with some novel functions.Singular solutions derived from[Williams(1952)]biharmonic stress potential are implemented to the 2-D hybrid-Trefftz elements to model high stress gradients[Freitas and Ji(1996a)]and crack problems[Freitas and Ji(1996b)].Exploring the clouds concept to define a support region[Duarte,Babuška and Oden(2000)],the enrichment of the initial approximation stress bases is introduced in the hybrid-Trefftz formulation for plane elasticity by[Souza and Proença(2011)].Singularities in crack problems are analyzed by Trefftz elements with collocation method by[Li,Lu and Hu(2004)].

Construction of appropriate models for heterogeneous materials may involve a formidable task due to the presence of numerous voids or inclusions and,consequently,the stress concentration around them.To deal with such issue in an attractive manner,[Dong and Atluri(2012a,b,c)]develop micro mechanical models based on special Trefftz elements with built-in voids or inclusions.

[Freitas and Bussamra(2000)]have presented hybrid-Trefftz stress elements for the analysis of three-dimensional elastic problems:6-face elements(hexahedrons)and 4-face elements(tetrahedrons).The stress bases are extracted from the Papkovitch-Neuber solution of Navier equations for isotropic material,assigning Legendre and Chebyshev polynomials to Papkovitch-Neuber potentials.These elements have shown good performance in the analysis of three-dimensional solids:no locking in the incompressibility or near incompressibility regime,low sensitivity to ele-ment distortion(deviation from a right-angle hexahedron)and good estimates for stresses and displacements.In special,very low sensitivity to high aspect ratio(ratio between the largest and smallest element edges)was reported for the hexahedral elements in modeling thin plates.This formulation has been extended to the elastoplastic analysis of solids[Bussamra,Pimenta and Freitas(2001)]and to the analysis of laminated composite plates[Bussamra,Lucena Neto and Raimundo(2012)].

The above element attributes,in addition to the symmetry,high sparsity and well conditioning of the solving system,have motivated the use of the hexahedral elements presented by[Freitas and Bussamra(2000)]to handle thin plates with geometric discontinuities.Solution of stress concentration problems is carried out and comparison of the obtained stress concentration factors and stress intensity factors is made with available results.The hierarchicalp-refinement strategy is exploited in the numerical tests.It is shown that good results can be directly computed with relatively coarse meshes.

2　Finite element formulation

LetV be the domain of a typical finite element and Γ its boundary.Let Γuand Γσbe the portions of Γ on which displacements and tractions are specified,respectively.The equilibrium equations and strain-displacement relations are

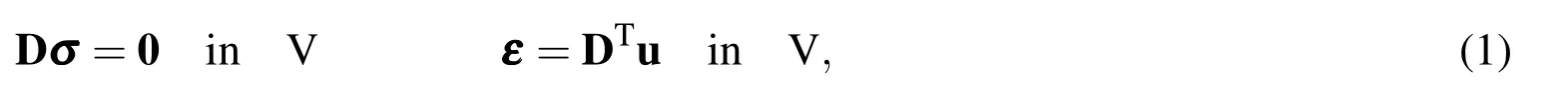
whereuis the displacement vector,σandεare vectors which collect the independent components of stress and strain tensors andDis a differential operator.Body forces and residual stress are not taken into account for simplicity.On the boundary,

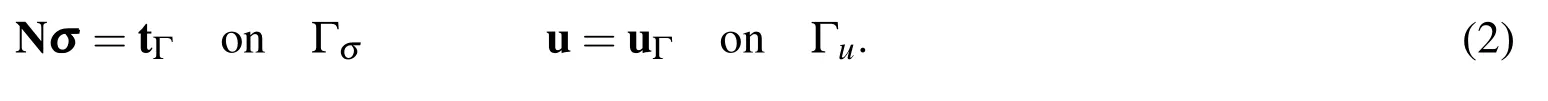
MatrixNcontains the components of the unit outward normal vector to Γ;vectorstΓanduΓare the specified surface tractions on Γσand displacements on Γu.The stress-strain relations of a linearly hyperelastic material are denoted by

wherekis the 6×6 material stiffness matrix.

2.1　Approximations

The Hybrid-Trefftz elements are based on the direct and independent approximations of stressσin V and displacementonΓσand also on the interelement bound-ary

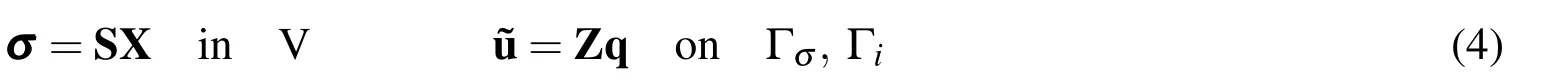
MatricesSandZcollect the approximation functions and vectorsXandqcollect the corresponding weights.

The equilibrium equations can be expressed in terms of the displacement field by

known as Navier equations.Trefftz constraint requires a choice ofSsuch thatuwithin the element satis fies(5).The stress is then determined from the displacement by means of

If the displacement is w ritten as

whereurcollects the rigid-body displacement components andUcollects functions related to the displacement basis,one gets from(4)and(6)

2.2　On the choice of U

Each column ofUis stated as a Papkovitch-Neuber solution of(5)for isotropic material:

whereψandφare vector and scalar harmonic displacement potentials,respectively,rthe position vector,∇ the gradient operator andνthe Poisson’s ratio[Slaughter(2002)].

Legendre and Chebychev polynomials are attributed toψandφ,as explained in[Freitas and Bussamra(2000)],in order to generate a displacement basisU.Linearly dependent modes,i.e.,linearly dependent columns ofU,eventually introduced in this process are eliminated.The stress basis(8)is then described by 186 complete,linearly independent polynomial modes of degree dσ=6.Higher degrees are possible,but incomplete bases are generated.For degrees 7,8 and 9,for instance,the stress bases have 231,278 and 326 independent modes with deficits of 6,16 and 31 modes to be completed,respectively.

A complete polynomial basis of degree dσ≤6 is explicitly written in the computer code.In this case,linearly dependent modes generated by Legendre and Chebyshev associated polynomials have been detected and eliminateda priorifrom the stress basisS.For greater polynomial degrees dσ＞6,polynomials are recursively calculated so that linearly dependent modes detection and elimination are performed during the solving system solution,when a zero,or an almost zero,pivot is found in the Gauss elimination process.Construction of complete and linearly independent sets of Papkovich-Neuber solutions in polynomial form can be found in[Fu,Yuan,Cen and Tian(2012);Wang,Xu and Zhao(2012)].

2.3　On the choice of Z

Displacements on Γσand Γiare approximated by independent hierarchical monomial bases,following the Pascal’s triangle scheme in a local coordinate system(ζ1,ζ2)with−1≤ζi≤1,assigned to each one of the 6 faces of the master cubic element[Cook,Malkus,Plesha and Witt(2002)].As there are three displacement components,the number of independent displacement modes on each face is

for a polynomial of degreen.

2.4　Element matrices

The element is based on the variational expressions

which require that the approximation of the stress fieldσmust be extracted from the Navier equation solution and the approximation of the displacement fieldmust be the same along the common boundaries of any two adjacent elements[Washizu(1982);Fung and Tong(2001);Wunderlich and Pilkey(2002)].There is no other constraint to be satisfied.

The divergence theorem allows to w rite

which reduces to

sinceDTurandDδ σare both null vectors.In view of(13),substitution of the approximations(4)and(7)into(11)yields the discrete equations

or

where

All integrals in(16)are exactly integrated by Gauss-Legendre quadrature with the minimum number of points required.

Asσis chosen independently for each element,Xcan be eliminated from the element equation(15),

by assuming that the matrixFis nonsingular,to give

LetnXandnqbe the number of stress and displacement parameters inXandq.Then

where 6 is the number of rigid body modes associated with the basisZ.The rank of the matrix w ill be deficient and there w ill be spurious modes ifnX＜nq−6[Fung and Tong(2001)].In accordance with[Pian(1995);Pian and Wu(2006)],suppression of spurious modes,as it is done in this paper whenever a linearly dependent mode is detected,is the practical procedure for satisfying the mathematical form of a stability criterion,namely the LBB condition[Babuška(1973);Brezzi(1974)].The restrictionnX＜nq−6 for an individual element is necessary,but not sufficient,to ensure the satisfaction of the LBB condition.

A hybrid element becomes stiffer as the numbernXincreases,and usually becomes more flexible as the numbernqincreases.One cannot say in general that a model built of hybrid elements w ill be either stiffer or more flexible than the mathematically exact solution.The optimal relation betweennXandnqshould be found by numerical experimentation.

Some comments are in order on the numerical solution of the assembled set of equations of a finite element model.Because the assembled square matrix is symmetric and highly sparse,substantial memory is saved by storing only its nonzero entries,located in the upper triangle,in a three-column matrix with each row containing a nonzero entry and its position(row and column)in the original square matrix.Sparsity,defined as the ratio between the number of zero elements of the square matrix and its total number of elements,is typically greater than 99%.Symbolic Cholesky decomposition is applied to reduce fill-in,and then direct Gauss elimination method is applied to find the solution[Pissanetsky(1984)].

To increase the sparsity and also improve the conditioning a little more,the origin of the local Cartesian coordinate system is positioned at each element centroid.Material properties and geometric dimensions are scaled properly and advantage has been taken of the fact that identical elements,wherever are placed,have the same sub matrixF.

3　Numerical tests

Three examples have been chosen to illustrate the performance of the hybrid-Trefftz formulation in the analysis of stress concentration in plates subjected to a uniformly distributed edge loadq.All the examples are three-dimensional models of isotropic rectangular plates with thicknessh,lengthL,widthH,Young’s modulusEand Poisson’s ratioν.The relevant data for the numerical analysis are summarized in Tab.1(consistent units are used).Although just one layer of elements is adopted in the thickness direction,the discretization can still be improved underp-refinement in that direction.

Neither the formulation nor the approximation bases constrain the element geometry,which may be non-convex or multiple connected.However,and for simplicity,only one cubic master element is employed.

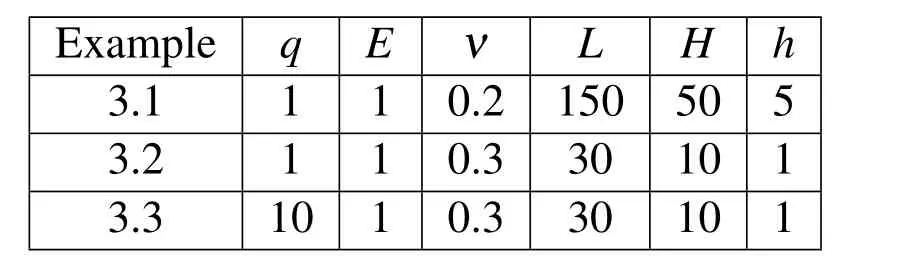
Table 1:Data for the numerical analysis

Several hybrid-Trefftz stress elements,identified by HTS(dσ,du),are tested.The symbol dustands for the degree adopted for displacement polynomial approximation in each element face and dσ,as already defined,is the degree of the stress polynomial approximation.Elements with dσ＞6 w ill involve incomplete stress basis.

3.1　Notched plate

The first set of tests is concerned with stress concentration factor calculation in a double notched plate,as depicted in Fig.1.The plate has half-circular notches with radiusr,the left edge fixed and the right one submitted to the action of a uniformly distributed loadq,and refers to a Cartesian coordinate system with thexy-plane located in the plate midsurface.

Figure 1:Notched plate.

Figure 2 shows the meshes used in the notched plate analysis,with 38,36 and 52 elements.The convergence of the stress concentration factorKtis verified with different degrees of polynomial stress approximation dσin the element domain and displacements duin the element boundary.The stress concentration factor is defined as the ratio between the maximum stressσxx,evaluated in the plate midsurface atorand the nominal stressFigure 3 summarizes the results forKt/Ktnobtained withr=0.4H,where the reference valueKtn=1.141 is taken from

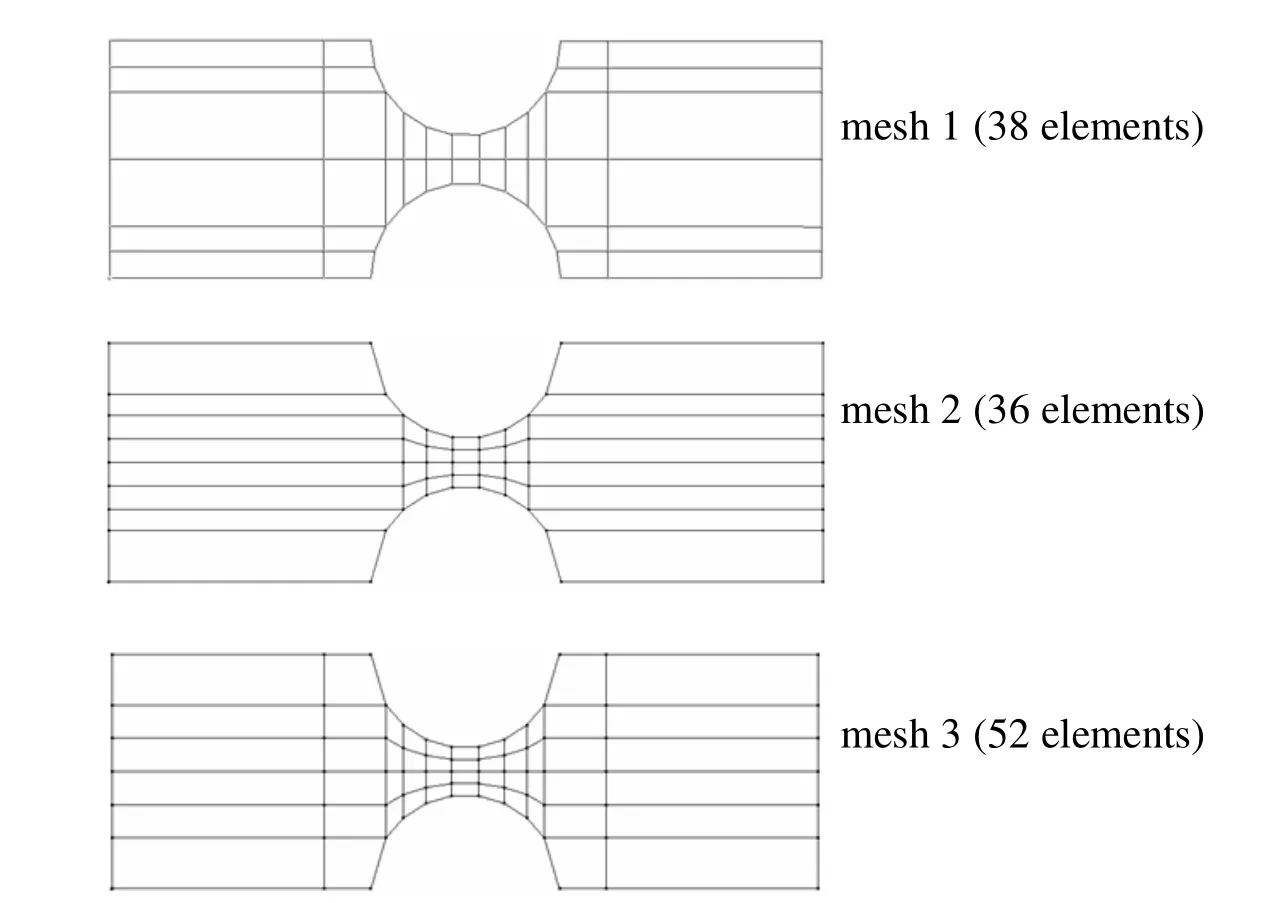
Figure 2:Meshes for the notched plate problem.

given by[Pilkey and Pilkey(2008)]for an in finitely long plate in a state of plane stress.

The contour ofσxx/qdepicted in Fig.4 shows that the notches are sufficiently far from the edgesx=0 andx=Lto make insignificant the influence of longer plates on the calculatedKt.

The midsurface distribution ofσxx/σnalong the plate width atx=L/2 is plotted in Fig.5a in a suitable scale to highlight the small interelement discontinuity.At this point it should be remembered that the interelement traction continuity is enforced to be satisfied only in a weak sense according to(11).It is also plotted in Fig.5b the distribution ofσxx/σnalong the plate thickness at(x,y)=(L/2,r)or(L/2,H−r),where the maximum valueσxx/σn=1.144 for the whole plate is shown.Finally,results ofKt/Ktngiven in Tab.2 using different values ofr/Hcon firm the good performance of HTS(9,4)element in mesh 2.Although this model has 21501 degrees of freedom,the computing time to solve the linear system was 14 s due to the advantage taken from the 99.42%matrix sparsity.The numerical tests was carried out in a PC-Computer with Intel Core Duo 2.93 GHz,8 GB RAM,running Windows XP.

Figure 3:Results of for r=0.4 H under p-refinement.

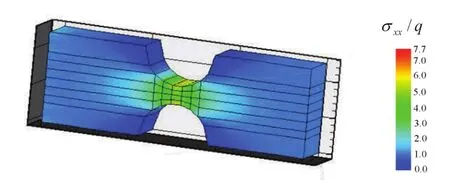
Figure 4:Contour of σxx/q for r/H=0.4 obtained with mesh 2 of HTS(9,4)elements.

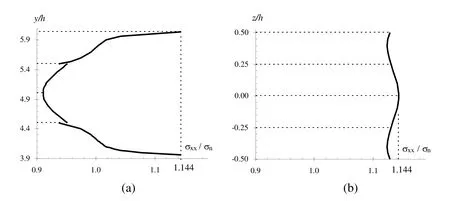
Figure 5:Distribution of σxx/σn for r=0.4 H obtained with mesh 2 of HTS(9,4)elements:(a)in the midsurface along the plate width at x=L/2;(b)along the plate thickness at(x,y)=(L/2,r)or(L/2,H–r).

3.2　Cracked plate

In the second set of tests,the stress intensity factorKIis evaluated for the cracked plate depicted in Fig.6.The notches of Fig.1 are replaced by one crack of lengthaand the 48-element mesh of Fig.7 is used in the analysis.

As the plate is in a state of plane stress,the stress intensity factor is evaluated by means of

Figure 6:Cracked plate.

Figure 7:48-element mesh for the cracked plate problem.

The strain energy release rate

has the derivative∂U/∂anumerically replaced by the ratio between the strain energy change ΔUand the small value Δaassigned to the crack extension.In the present finite element formulation,the strain energy is evaluated from

in whichFrefers to the assembled equation that comes from each element contribution(15)andXresults from the equation solution.The stress intensity factors for several crack lengths obtained with 48-element mesh underp-refinement are compared in Tab.3 with

found in[Tada,Paris and Irw in(2000)].Figure 8 shows the contour ofσxx/qin a small region around the crack tip forobtained with mesh of HTS(6,3)elements.Although this model has 12798 degrees of freedom,it involves a 99.81%sparse matrix.

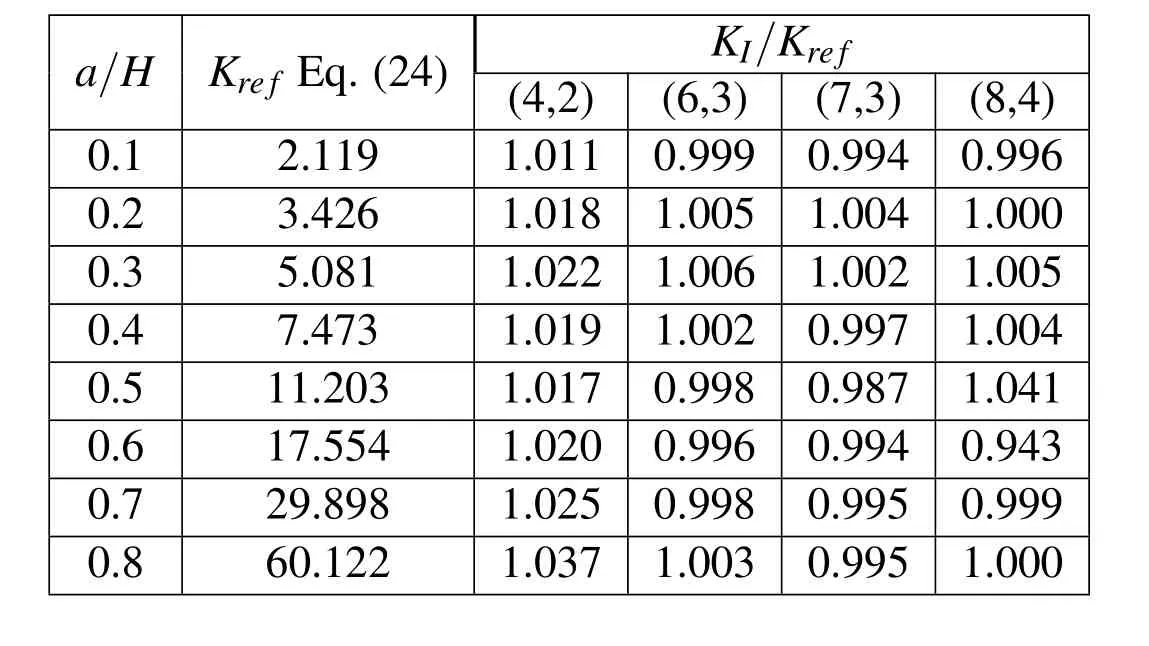
Table 3:Stress intensity factors obtained with 48-element mesh under p-refinement

Figure 8:Contour of σxx/q around the crack tip for a/H=0.5 obtained with mesh of HTS(6,3)elements.

3.3　Kinked crack plate

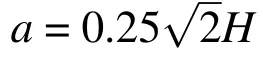
Figure 10:36-element mesh for the kinked crack plate problem

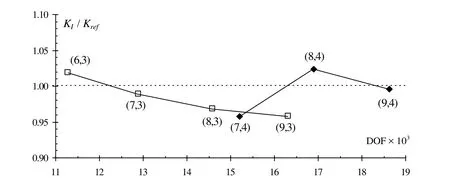
Figure 11:Results of KI/Kref under p-refinement.

is found in[Tracey and Cook(1977)].

The result obtained with mesh of HTS(9,4)elements are compared in Tab.4 with results obtained using special crack element models.The HTS(9,4)model has 16893 degrees of freedom,but deals with a 99.65%sparse matrix.

Table 4:Stress intensity factor KI.

4　Conclusions

The results show that the hexahedral hybrid-Trefftz elements can handle three-dimensional modeling of thin plates with geometric discontinuities.Good convergence rates under p-refinement are observed even for coarse meshes around the discontinuities.Accurate estimates for stress concentration factors and stress intensity factors are found.Many degrees of freedom are involved,but substantial memory and computing time are saved in the assemblage and problem solution by taking numerical advantage of the high sparsity,that has been greater than 99%.

Babuška,I.(1973):The finite element method with Lagrange multipliers.Numer Math,vol.20,no.3,pp.179-192.

Bathe,K.J.(1996):Finite element procedures.Prentice Hall,Englewood Cliffs.

Brezzi,F.(1974):On the existence,uniqueness and approximation of saddle point problems arising from Lagrangian multipliers.RAIRO,vol.8,no.2,pp.129-151.

Bussam ra,F.L.S.;Lucena Neto,E.;Raimundo Jr.,D.S.(2012):Hybrid quasi-Trefftz 3-D finite elements for laminated composite plates.Comput Struct,vol.92-93,pp.185-192.

Bussam ra,F.L.S.;Pimenta,P.M.;Freitas,J.A.T.(2001):Hybrid-Trefftz stress elements for three-dimensional elastoplasticity.Comput Assist Mech Eng Sci,vol.8,pp.235-246.

Cook,R.D.;Malkus,D.S.;Plesha,M.E.;W itt R.J.(2002):Concepts and applications of finite element analysis.John W iley,New York.

Dong,L.;Atluri,S.N.(2012a):Development of 3D T-Trefftz Voronoi cell finite elements with/without spherical voids&/or elastic/rigid inclusions for microme-chanical modeling of heterogeneous materials.Comput Mater Contin,vol.29,no.2,pp.169-211.

Dong,L.;Atluri,S.N.(2012b):Development of 3D Trefftz Voronoi cells with ellipsoidal voids&/or elastic/rigid inclusions for microme-chanical modeling of heterogeneous materials.Comput Mater Contin,vol.30,no.1,pp.39-81.

Dong,L.;Atluri,S.N.(2012c):T-Trefftz Voronoi cell finite elements with elastic/rigid inclusions or voids for m icromechanical analysis of composite and porous materials.Comput Model Eng Sci,vol.83,no.2,pp.183-219.

Duarte,C.A.;Babuška,I.;Oden,J.T.(2000):Generalized finite element methods for three-dimensional structural mechanics problems.Comput Struct,vol.77,no.2,pp.215-232.

Freitas,J.A.T.;Bussam ra,F.L.S.(2000):Three-dimensional hybrid-Trefftz stress elements.Int J Numer Meth Engng,vol.47,no.5,pp.927-950.

Freitas,J.A.T.;Cismasiu,C.(2001):Developments with hybrid-Trefftz stress and displacement elements.Comput Assist Mech Eng Sci,vol.8,pp.289-311.

Freitas,J.A.T.;Ji,Z.Y.(1996a):Hybrid-Trefftz finite element formulation for simulation of singular stress fields.Int J Numer Meth Engng,vol.39,no.2,pp.281-308.

Freitas,J.A.T.;Ji,Z.Y.(1996b):Hybrid-Trefftz equilibrium model for crack problems.Int J Numer Meth Engng,vol.39,no.4,pp.569-584.

Fu,X.R.;Yuan,M.W.;Cen,S.;Tian,G.(2012):Characteristic equation solution strategy for deriving fundamental analytical solutions of3D isotropic elasticity.Appl Math Mech,vol.33,no.10,pp.1253-1264.

Fung,Y.C.;Tong,P.(2001):Classical and computational solid mechanics.World Scientific,Singapore.

Hinton,E.;Cam pbell,J.S.(1974):Local and global smoothing of discontinuous finite element functions using a least squares method.Int J Numer Meth Engng,vol.8,no.3,pp.461-480.

Hinton,E.;Scott F.C.;Ricketts,R.E.(1975):Local least squares smoothing for parabolic isoparametric elements.Int J Numer Meth Engng,vol.9,no.1,pp.235-256.

Kardestuncer,H.(1988):Finite element handbook.M cGraw-Hill,New York.

Li,Z.C.;Lu,T.T.;Hu,H.Y.(2004):The collocation Trefftz method for biharmonic equations with crack singularities.Eng Anal Bound Elem,vol.28,no.1,pp.79-96.

M aiti,S.K.(1992):A finite element for variable order singularities based on the displacement formulation.Int J Numer Meth Engng,vol.33,no.9,pp.1955-1974.

Pian,T.H.H.(1995):State-of-the-art development of hybrid/mixed finite element method.Finite Elem Anal Des,vol.21,no.1-2,pp.5-20.

Pian,T.H.H.;Wu,C.C.(2006):Hybrid and incompatible finite element methods.Chapman,Boca Raton.

Pilkey W.D.;Pilkey,D.F.(2008):Peterson’s stress concentration factors.John Wiley,Hoboken.

Pissanetsky,S.(1984):Sparse matrix technology.Academic Press,London.

Slaughter,W.S.(2002):The linearized theory of elasticity.Birkhäuser,Boston.

Souza,C.O.;Proença,S.P.B.(2011):A hybrid-Trefftz formulation for plane elasticity with selective enrichment of the approximations.Int J Numer Meth Biomed Engng,vol.27,no.5,pp.785-804.

Tada,H.;Paris,P.C.;Irw in,G.R.(2000):The stress analysis of cracks handbook.ASME Press,New York.

Tracey,D.M.;Cook,T.S.(1977):Analysis of power type singularities using finite elements.Int J Numer Meth Engng,vol.11,no.8,pp.1225-1233.

Wang,M.Z.;Xu,B.X.;Zhao,Y.T.(2012):General representations of polynomial elastic fields.J Appl Mech,vol.79,no.2,pp.021017-1-021017-8.

Washizu K(1982):Variational methods in elasticity and plasticity.Pergamon Press,Oxford.

W illiam s,M.L.(1952):Stress singularities resulting from various boundary conditions in angular corners of plates in extension.J Appl Mech,vol.19,pp.526-528.

Wunderlich,W.;Pilkey,W.D.(2002):Mechanics of structures:variational and computational methods.CRC Press,Boca Raton.