Forced Vibrations of a System Consisting of a Pre-strained Highly Elastic Plate under Compressible Viscous Fluid Loading

1 Introduction

Investigations of problems related to the dynamics of plate- fluid interaction have great significance in the theoretical and application sense in aerospace,nuclear,naval,chemical and biological engineering.The first attempt in this field was made by Lamb(1921)in which vibration of a circular elastic “baf fled”plate in contact with still water were considered.It was assumed that this plate is clamped all around and placed in a matching circular aperture within an in finite rigid plane wall.The investigations were made by the use of the so-called“non-dimensional added virtual mass incremental”(NAVM I)method,according to which,it is assumed that the modes of vibration of the plate in contact with still water are the same as those in a vacuum,and the natural frequency is determined by the use of the Rayleigh quotient.In this case it is supposed that the squares of the natural frequencies of the plate are equal to the ratio between the maximum potential energy of the plate and the sum of the kinetic energies of both the plate and the fluid.Later this method was employed in many related investigations such as in papers by Kwak and Kim(1991),Fu and Price(1987),Zhao and Yu(2012)and in many others listed in these papers.Up to now there are also the investigations carried out without employing the NAVMI method.For instance,in a paper by Tubaldi and Armabili(2013)the vibration and stability of the rectangular plate immersed in axial liquid flow was studied without employing the NAVMI method,and the Galerkin method was applied to determine the expression of the flow perturbation potential.Then the Rayleigh-Ritz method was used to discretize the system.

Investigations carried out in a paper by Charman and Sorokin(2005)and others listed therein were also made without employing the NAVM I method.Note that in this paper the forced bending vibration of an in finite plate in contact with compressible(acoustic)inviscid fluid,where this fluid occupies a half-plane(half-space),was considered.This paper gives asymptotic analyses of the sound and vibration in the metal plate and compressible inviscid fluid system.

The other aspect of investigations related to the plate- fluid interaction regards wave propagation problems.Investigations carried out in a paper by Sorokin and Chubinskij(2008)and others listed therein can be taken as examples of this.It should be noted that before this paper the problems of time harmonic linear wave propagation in elastic structure- fluid systems were investigated within the framework of the theory of compressible inviscid fluid.A list of these studies and a review is given in the aforementioned paper by Sorokin and Chubinskij(2008).At the same time,the role of fluid viscosity in wave propagation in the plate- fluid system was first investigated in this paper.However,in this paper and all the papers indicated above,the equations of motion of the plate were written within the scope of the approximate plate theories by the use of various types of hypotheses such as the Kirchhoff hypotheses for plates.Consequently,the use of the approximate plate theories in these investigations decreases significantly the analyzed range of wave modes and their corresponding dispersion curves.It is evident that in many cases(for instance,in the cases where the wave length is less significant than the thickness of the plate)more accurate results in the qualitative and quantitative sense,can be obtained by employing the exact equations for describing plate motion.Moreover,in the foregoing investigations(except the paper by Zhao and Yu(2012))the initial strains(or stresses)in plates,which can be one of their characteristic particularities,are not taken into account.These two characteristics,namely the use of the exact equations of plate motion and the existence of initial stresses in the plate are taken into consideration in a paper by Bagno et al.(1994)and others,a review of which is given in a survey paper by Bagno and Guz(1997).Note that in these papers,in studying wave propagation in pre-stressed plate+compressible viscous fluid systems,the motion of the plate was written within the scope of the so-called three-dimensional linearized theory of elastic waves in initially stressed bodies(TLTEWISB).However,the motion of the viscous fluid was written within the scope of the linearized Navier-Stokes equations.Detailed consideration of related results was made in the monograph by Guz(2009).

However,up to now within this framework there is not an investigation related to the forced vibration of the pre-strained plate+compressible viscous fluid system.In the present paper the attempt is made in this field and two-dimensional(plane-strain state)problem on the forced vibration of the pre-strained plate made of highly-elastic material+compressible viscous fluid system is studied.The motion of the plate is described by utilizing of the TLTEW ISB,and the motion of the fluid by utilizing of the linearized Navier-Stokes equations.Numerical results on the velocity and stress distributions on the plate- fluid interface and the influence of the problem parameters such as initial strains of the plate,the thickness of the plate,the frequency of the external force etc.on these distributions are presented and discussed.These results are obtained in the case where the fluid is Glycerin and the values of the elastic constants which enter into the mentioned above harmonic potential and the density of the plate material are taken as Lame’s constants and density of the Plexiglass(Lucite).Consequently,in the case where the initial strains is absent in the plate the numerical results relate to the hydro-elastic system consisting of the Plexiglass and Glycerin.Note that corresponding problems related to the pre-strained plate+elastic halfspace were studied in papers by Akbarov(2006 a,b,2013a)Akbarov and Guler(2007),Akbarov et al(2005),Akbarov and Ilhan(2009,2010),Akbarov et al(2013)and Emiroglu et al(2009).

2 Formulation of the problem and governing field equations

Consider a system consisting of an initially stretched plate-layer which is in contact with the half-space occupied by the compressible Newtonian viscous fluid(Fig.1).Assume that the thickness of the plate in the natural state(i.e.before the initial stretching of that)ish.We consider separately the governing field equations for the plate-layer and for the compressible Newtonian viscous fluid

2.1 Governing field equations for the plate-layer.

In the natural state,we determine positions of the points of the layer by the Lagrangian coordinates in the Cartesian system of coordinatesOx1x2x3.Suppose that the layer has in finite length in the directions of theOx1andOx3axes.TheOx3axis extends along a direction perpendicular to the planeOx1x2in Fig.1 and therefore in not shown in this figure.

We propose that the layer made of highly-elastic material,before being contacted with fluid,be stretched along theOx1axis direction and as result of this stretching the homogeneous finite strain state appears in the layer.Namely this strain state is called the initial strain state in the layer.Note that the initial strains are caused by the static forces acting in theOx1axis direction at infinity and the action of these forces continues all further dynamic process.

Figure1:The sketch of the system under consideration (a) and Sommerfeld contour(b).

With the initial state of the layer we associate the Lagrangian Cartesian system of coordinatesOy1y2y3and suppose that the origin of the system coincides with the origin of the systemOx1x2x3,and the coordinate axesOy1,Oy2andOy3coincide with the coordinate axesOx1,Ox2andOx3,respectively.Assuming that the material of the layer is compressible,the elastic relations are given through the harmonic potential.

Below the values related to the initial state are denoted by upper index 0.Thus,according to the foregoing,the initial state in the layer can be determined as follows.

whereis a component of the displacement vector in the layer in the initial strain state andλkis an elongation factor which characterizes the change in the length of the line element in theOxkaxis direction.This parameter determined by the expressionwhereεis thek-thprincipal value of thekGreen’s strain tensor.The expression of the components of this tensor through the components of the displacement vector will be given below.

Within this consider a motion of the layer in the case where on the free face plane of that the line-located normal time harmonic force acts.This consideration will be made by the use of coordinates associated with the initial state,i.e.by the use of coordinatesyk(k=1,3),in the framework of the three-dimensional linearized theory of elastic waves in initially stressed bodies(TLTEWISB).In the construction of the field equations of the TLTEWISB,one considers two states of a deformable solid.The first is regarded as the initial or unperturbed state and the second is a perturbed state with respect to the unperturbed one.By the“state of a deformable solid”both motion and equilibrium(as a particular case of motion)is meant.It is assumed that all values in a perturbed state can be represented as a sum the values in the initial state and the perturbations.The latter is also assumed to be small in comparison with the corresponding values in the initial state.It is also assumed that both initial(unperturbed)and perturbed states are described by the equations of nonlinear solid mechanics.Owing to the fact that the perturbations are small,the relationships for the perturbed state in the vicinity of appropriate values for the unperturbed state are linearized,and then the relations for the perturbed state are subtracted from them.The results is the equations of the TLTEWISB.The general problems of the TLTEWISB have been elaborated in many investigations such as Biot(1965),Guz(2004),Truestell and Noll(1965)and others.

Thus,the following are the basic relations of the TLTEWISB for the compressible body under the plane-strain state in theOy1y2plane.

The equation of motion is

and mechanical relations are

wherei;j;α;β=1,2 and Einstein summation rule is employed with respect to the repeated indices in(2)and(3).Moreover,in equation(2)and(3)the following notation is used:Qijare the components of the perturbations of the Kirchhoff non-symmetric stress tensor related to the areas of the initial state,ujare the components of the perturbations of the displacement vector,andρis the density also related to the volume of the initial state.Expressions for determination of the componentsωijαβwill be determined below.Note that these components are determined through the initial strain state(1)and through the elastic potential.As has noted above,in the present work the elastic relations of the layer’s material are determined by harmonic potential.This potential is given as follows:

whereλandµare the mechanical constants of the material and

In(5)εi(i=1,2,3)are the principal values of the Green’s strain tensor.

Let us consider briefly the definition of the stress and strain tensors in the large elastic deformation theory which are used in the present investigation.For this purpose we use the Lagrange coordinatesxi(i=1,2,3)in the Cartesian system of coordinatesOx1x2x3and the position of the points after and before deformations we determine by the vectorsr∗andrrespectively wherer∗=r+u.Hereu=uigiis a displacement vector expressed by the unit basic vectorsgi.Taking the relations(here the symbol"·"means the scalar product of the vectors),

This is a component of the Green’s strain tensorwhich is symmetric.

Let us consider the definition of the Kirchhoff stress tensor.The use of various types of stress tensors in the large( finite)elastic deformation theory is connected with the reference of the components of these tensors to the unit area of the relevant surface elements in the deformed or un-deformed state,because,in contrast to the linear theory of elasticity,in the finite elastic deformation theory the difference between the areas of the surface elements taken before and after deformation must be accounted for in the derivation of the equation of motion and under satisfaction of the boundary conditions.According to the aim of the present investigation,we here consider two types of stress tensors denoted byandthe components of which refer to the unit area of the relevant surface elements in the un-deformed state,but act on the surface elements in the deformed state.The componentsSijof the stress tensorare determined through the strain energy potentialwhereεijis a component of the Green’s strain tensor(6),by the use of the following expression:

The componentsqijof the stress tensor˜qare determined by the expression

Hereis the Kronecker symbol.The stress tensor˜qwith components determined by expressions(7)and(8)is called the Kirchhoff stress tensor.According to expressions(6)-(8),the stress tensor˜Sis symmetric,but the Kirchhoff stress tensor ˜qis non-symmetric.Thus,with this we restrict ourselves to consideration of the definition of the stress and strain tensors in the finite elastic deformation theory.These definitions are given without any restriction related to the association of the selected coordinate systems to the natural or initial state.However,in using the coordinate system associated system with the initial deformed state,the initial strain state can be taken as an “un-deformed”state in the foregoing definitions.

Now we attempt to attain the Eq.(3)and the expressions of the componentsωijαβby employing the linearization procedure.Thus,according to(1),(4)-(8),we attain that

It follows from the second expression in(9)that

In this way,for a selected material the magnitude of the initial strains and the initial stresses in the layer can be determined throughλ1only.In this case the perturbation of the components of the non-symmetric Kirchhoff stress tensorqij(denoted byrelated to the areas of the natural state are determined by the following expression:

whereis a perturbation of the components of the foregoing stress tensor

By linearization of Eq.(7),the following relation is obtained for these components:

Using the relations

Taking the relations

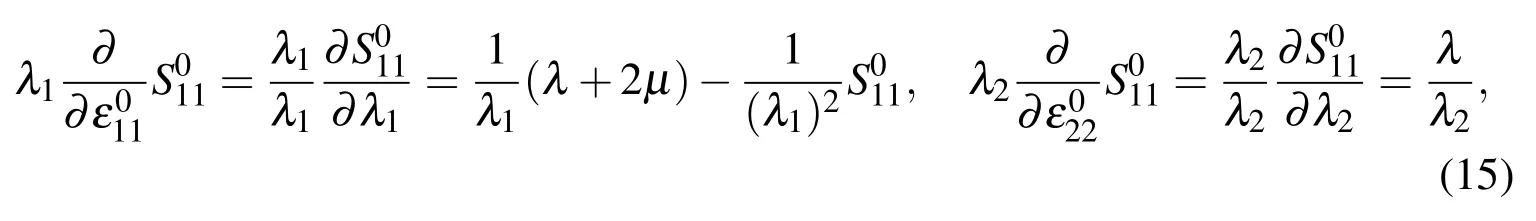
which are obtained from the definition of the parameterλiand expression forin Eq.(9),and the relations(14)into account,the following mathematical transformations can be made:

Thus,we obtain the foregoing expressions for componentsω1111andω1122.In this way we obtain the expressions for remain componentsωijαβin Eq.(3)which are differ from zero.These expressions are:

Note that the similar discussions of the equations and relations for the circular cylinders in the cylindrical system of coordinates have also been made in a paper by Akbarov(2013b).

Thus with this we restrict ourselves to consideration of the basic equations and relations within the scope of which the motion of the plate-layer is described.In this case the boundary conditions on the upper face plane of the layer can be written as follows.

In(18)ωis a frequency of the lineal-located external load with amplitudeP0,δ(y1)is a delta Dirac function.

2.2 Governing field equations for the compressible Newtonian viscous fluid.

Now we consider the field equations of motion of the Newtonian compressible viscous fluid and the density,viscosity constants and pressure related to that we will denote by upper index(1).We use the Euler coordinates in the coordinate systemOy1y2y3which is associated with the initial state of the layer to write these equations.Taking the smallness of the perturbations in the perturbed state in the system under consideration we will identify the Euler and Lagrange coordinates in the coordinate systemOy1y2y3.Thus,within the foregoing assumptions,according to Guz(2009),we write field equations for the fluid flow.

The linearized Navier-Stokes equations:

The equation of continuity:

Rheological relations:

where

The equation of state:

In Eqs.(19)-(23)i;j;k=1,2,3 and the following notation is used:viis a component of a perturbation of the velocity vector,p(1)is a perturbation of the pressure,µ(1)is a coefficient of viscosity,λ(1)is the second coefficient of the viscosity,a0is a sound speed in the fluid,eijis a component of a perturbation of the strain rate tensor,Tijis a component of a perturbation of the stress tensor,ρ(1)is a perturbation of the density of the fluid,is a density of the fluid in the initial state,i.e.before the perturbation of the fluid andδijis a Kronecker symbol.Note that in Eqs.(19)-(21)Einstein summation rule is employed with respect to the repeated indices.In the present paper we consider the case where

According to Guz(2009),the solution of the system equations(19)-(23)in the case where the relations in(24)take place,is reduced to the finding of two potentialsφandψwhich are determined from the following equations.

The velocitiesv1,v2and the pressurep(1)are expressed via the potentialsφandψby the following expressions:

Assuming that,we obtain:

This completes the field equation of the fluid flow which is considered in the present paper.As fluid occupies the half-planewe assume that

and there is not reflected waves fromy2=-∞.

2.3 Contact conditions on the interface between the fluid and pre-strained layer

We assume that the velocities and forces acting on the interface between the fluid and layer are continuous.In other words,we assume that

This completes the formulation of the problem.It should be noted that,with corresponding obvious changes,the foregoing problem formulation can be remake for the case where the fluid is inviscid.Moreover,in the case whereλ1=λ2=1.0 the foregoing formulation relates to the corresponding classical problem of hydroelastodynamics.

3 Method of solution

Below,we use the dimensionless coordinatesand om it the over bar on the coordinates.According to the boundary condition(18),we represent the sought values as

Taking the problem symmetry with respect toy1=0 into account,we can represent the originals of the sought values as follows.

First,we consider the solution of the equations related to the Fourier transformation of the quantities related to the plate-layer,i.e.to the solution of the equations which are obtained from the equations(2),(3),(16)and(17)by employing Fourier transformation(32).Thus,substituting the expressions(32)into the equations(2)and(3),and doing some mathematical manipulations we obtain the following equations for theu1Fandu2F.

where

Introducing the notation

we can w rite the solution of the equation(33)as follows.

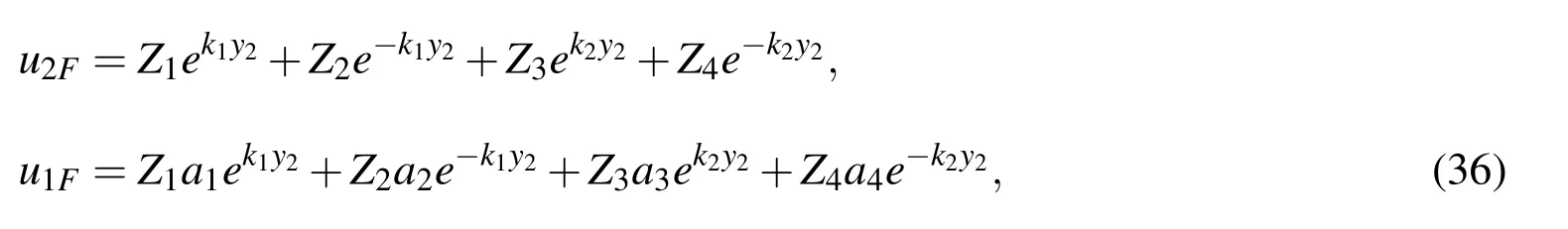
where

Using the equations(3)and(36)we also w rite expressions for the Fourier transformationsQ21FandQ22Fof the corresponding stresses which enter the boundary condition(18)and contact condition(29).

This completes the consideration of the determination of the Fourier transformation of the values related to the plate-layer.Now we consider the determination of the Fourier transformations of the quantities related to the fluid flow.First,we consider the determination of theφFandψFfrom the Fourier transformation of the equations in(25),which taking the relation(27)into account and the relation

can be written as follows

where

The dimensionless numberNwin(41)can be taken as Womersley number and characterizes the influence of the fluid viscosity on the mechanical behavior of the system under consideration.When the Womersley number is large(around 10 or greater),it shows that the flow is dominated by oscillatory inertial forces.When the Womersley number is low,viscous forces tend to dominate the flow.However,for hydro-elastodynamic problems the mentioned “large”and “low”limits for the Womersley number can change significantly.

The dimensionless frequency Ω1in(41)can be taken as the parameter which characterizes the compressibility of the fluid on the mechanical behavior of the system under consideration.Thus,taking the conditions(28)into consideration,the solutions to the equations in(40)are found as follows

where

Using(42)and(39)we obtain the following expressions for the velocities,pressure and stresses of the fluid from the Fourier transformations of the equations(21),(22)and(26).

where

Substituting expressions(36),(38)and(44)into the boundary condition(18)and contact condition(29)we obtain system of equations with respect to the unknownsZ1,Z2,...,Z6through which the sought values are determined.The mentioned equation can be expressed as follows.

where

The expressions of the coefficientsαnm(n;m=1,2,...,6)can be easily determined from expressions(36),(38)and(44),and therefore we do not give here these expressions.Thus,unknownsZ1,Z2,...,Z6in the equations(46)can be determined via the formulae.

Now we consider the calculation of the integrals in(32).For this purpose first we consider the following reasoning.If we take the Fourier transformation parametersas the wavenumber then the equation coincides with the dispersion equation of the waves propagated in the direction of theOy1axis in the system under consideration.It should be noted that,according to the well-known physic-mechanical considerations,the equation(49)must have complex roots only.This character of the roots is caused with the viscosity of the fluid.However,as usual,the viscosity of the Newtonian fluids is insignificant in the qualitative sense and therefore in many cases within the scope of the PC calculation accuracy the equation(49)has real roots.Consequently these roots become singular points of the integrated expressions in the integrals(32).Therefore,according to works by Lamb(1904),Tsang(1978),Jensen et al(2011)and many others listed in these references,we will evaluate the wavenumber integrals(32)along the Sommerfeld contour(Fig.1b)in the complex planes=s1+is2and in this way the real roots of Eq.(49)are avoided.

Thus,using the presentation(30),we can determine the sought values through the following two type relations.

According to Fig.1b,we can w rite the following relation.

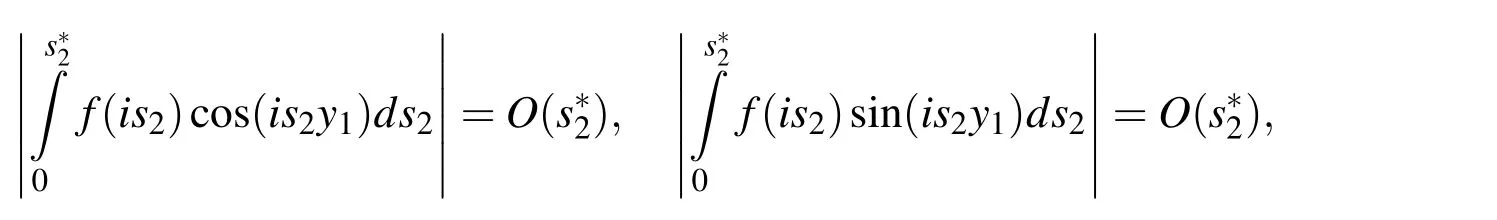
we use the following approximate expressions for calculation of the foregoing integrals

The accuracy of expressions in(52)with respect to values of the parameterwas discussed in a paper by Akbarov and Ilhan(2013).

This completes the discussions related to the algorithms employing for calculation of the wave-number integrals in the form(32).Note that after some obvious changing the foregoing solution method can be applied also for the case where the fluid is inviscid.

4 Numerical results and discussions

It follows from the foregoing discussions that the problem under consideration is characterized through the dimensionless parameters Ω1andNwwhich are deter-mined by the expressions in(41),Mwhich is determined with the expression(47),?whereλandµare the mechanical constants which enter the expression of the elastic potential(7),andλ1through which the initial strains in the layer are characterized.Note that the case where Ω1=0 corresponds to the incompressible fluid,but the case whereto the inviscid fluid.

Under numerical investigation we assume that the values of the mechanical constants and the density of the plate material areand?but the material of the fluid is Glycerin with viscosity coefficientdensityρ=1260kg?m3and sound speeda0=1459.5m/s[Guz(2009)].We introduce also the notationwhich is the shear wave propagation velocity in the layer material in the case where the initial strains are absent in that.Note that the values selected above for the constantsλ,µandρ,and related to the plate material under absent of the initial strains corresponds to the Plexiglass(or Lucite)[see Guz(2004);Lai-Yu et al(2006)].Consequently,these values have real meaning and numerical results attained in the case where the initial strains are absent in the plate,i.e.in the case whereλ1=λ2=1.0 in the linearized elastic relations(3),(16)and(17),can be regarded the hydro-elastic system consisting of the plate made of Plexiglass and half-plane filled by the Glycerin.

Thus,after the selection the values of materials constants the foregoing dimensionless parameters can be determined through the three quantities:h(the thickness of the plate-layer),ω(the frequency of the time-harmonic external forces)andλ1(the elongation parameter through which the initial strains in the layer are determined).In the present paper we will consider namely the influence of these three parameters on the distribution of the velocities and stresses on the interface plane between the pre-strained plate-layer and fluid.

With respect to the plate-layer thickness we consider two cases:the first case we call the“thin plate case”for which 0.001m≤h≤0.005m,but the second we call the“thick plate case”for which 0.05m≤h≤1.0m.For the“thin plate case”we assume that 5hz＜ω≤300hz,but for the“thick plate case”5hz＜ω≤1000hz.Before consideration of the numerical results we note the following reasoning.According to the mechanical consideration and a lot of numerical results(which are not given here),it can be predicted that the influence of the fluid viscosity on its motion in the case under consideration must be notable,namely in the"thin plate case"for low frequency of the forced vibration.But the influence of the fluid compressibility can be neglected in the “thin plate case”for the frequencies 5hz＜ω≤300hz,in other words in these cases the results obtained for the compressible and incompressible fluid models coincides with each other with very high accuracy.Also,according to the mechanical consideration,it can be predicted that the influence of the fluid compressibility on its motion must be considerable in the"thick plate case"under relatively high frequency of the forced vibration.Based on this reasoning we select the foregoing change range of the frequency for"thin"and"thick plate cases"and under obtaining numerical results related to the“thin plate case”we will assume that the fluid is compressible one.

Figure 2:The frequency response of T22(a),v2(b),v1(c,for a viscous fluid)and also v1(d,for an inviscid fluid)in the “thin plate case”under absent of the initial strains in the plate.

Figure 3:The distribution of T22(a),v2(b),v1(c,for a viscous fluid)and also v1(d,for an inviscid fluid)with respect to the y1/h in the “thin plate case”under absent of the initial strains.

Note that this conclusion agrees with the well-known mechanical considerations related to the influence of the viscosity of the systems on their vibration.

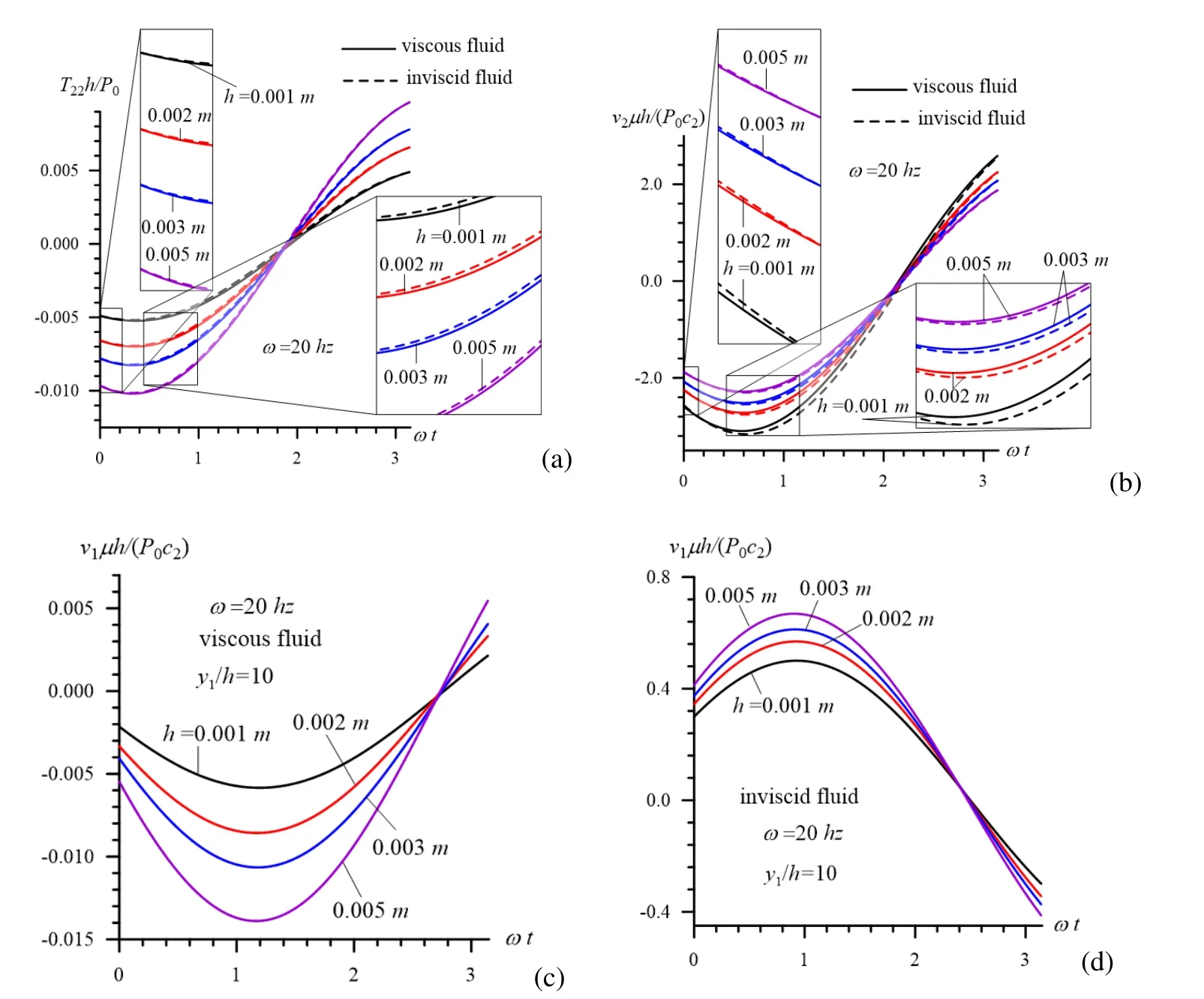
Figure 4:Graphs of the dependencies among T22(a),v2(b),v1(c,for a viscous fluid)and also v1(d,for an inviscid fluid)and ωt in the “thin plate case”under absent of the initial strains in the plate.

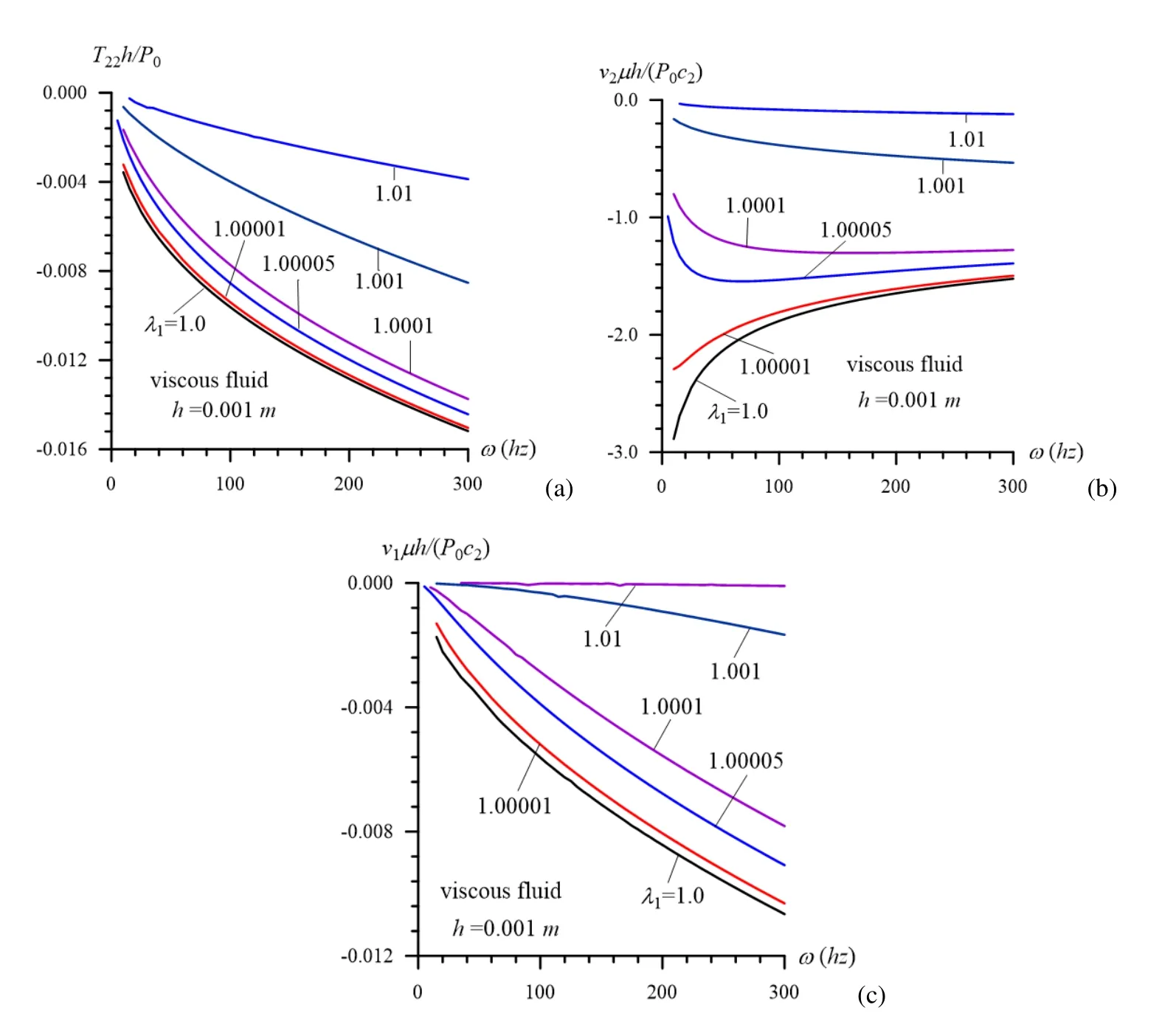
Figure 5:The influence of the initial stretching of the plate on the frequency response of T22(a),v2(b)and v1(c,for a viscous fluid)in the “thin plate case”under h=0.001m.

At the same time,it follows from the results given in Fig.2 that in the considered change range for the frequency the absolute values of theT22andv1increase,but the values of thev2decrease with the frequencyω.

Figure 6:The influence of the initial stretching of the layer(i.e.of the parameter λ1)on the dependencies among(b)and ωt.

According to the mechanical consideration the values of theT22,v2andv1must decay as?.This decay is observed for the stressT22and velocityv2from the Figs.3a and 3b,although this decay is very weak in the “thin plate case”and the magnitude of the decay increases with the plate thickness.Therefore the considerable illustration of the decay of the studied quantities with respect to the dimensionless coordinatewill be clearly illustrated under consideration the“thick plate case”.

We recall that the foregoing results are obtained from the expressions in(50)in the cases whereNow we consider numerical results related to the dependencies amongandωtin the case whereGraphs of these dependencies in the case whereλ1=1.0 are given in Figs.4a(forT22),4b(forv2),4c(forv1in the viscous fluid case)and 4d(forv1in the inviscid fluid case).It follows from these graphs that the absolute maximum values of the studied quantities arise in the cases whereIn other words,the absolute maximum values of the studied quantities arise atand the values of(ωt)∗can be easily determined from Fig.4 for each considered case.However,the absolute maximum values of the external loading arise,namely atThis means phase shifting of the studied quantities with respect to the external loading.It follows from Fig.4 that this phase shifting is more considerable for the velocitiesv2andv1.

Figure 7:The frequency response of T22(a),v2(b)and v1(c,for a viscous fluid)in the “thick plate case”under absent of the initial strains in the plate.

All the numerical results discussed above have been obtained in the case where the initial strains in the plate layer are absent.Consequently,the foregoing results can be related for the case where the plate material is a Plexiglass(Lucite)and the fluid is Glycerin.In other words,the foregoing results have real application field for the noted constituents of the system under consideration.Now we consider the results illustrated the influence of the initial strains of the plate on the frequency response of the studied quantities.For this purpose,we consider the graphs shown in Fig.5 which indicate the influence of the parameterλ1on the frequency response of theT22(Fig.5a),v2(Fig.5b)andv1(Fig.5c).It follows from Fig.5 that the initial stretching of the plate-layer causes to decrease the absolute values of the studied quantities significantly.Moreover,it follows from the Fig.5b that the initial stretching of the plate-layer effects also on the character of the frequency response of the velocityv2,i.e.for the relatively small values of the parameterλ1(for instance in the cases where)the absolute values of thev2increase,but for the relatively great values of the parameterλ1(for instance in the cases whereλ1≤1.00005)the absolute values of thev2decrease monotonically with the frequencyω.

Figure 8:The distribution of T22(a),v2(b),v1(c,for a viscous fluid)and also v1(d,for an inviscid fluid)with respect to the y1/h in the “thick plate case”under absent of the initial strains in the plate and under ω=600hz.

Also,we consider the influence of the initial stretching of the plate-layer on the dependence among?(Fig.6a),?(Fig.6b)andωt.It follows from Fig.6 that the initial stretching of the plate-layer causes to increase of the values of the phase shifting(ωt)∗.

Figure 9:Graphs of the dependencies among T22(a),v2(b)and ωt in the “thick plate case”under absent of the initial strains in the plate and under ω =600hz.

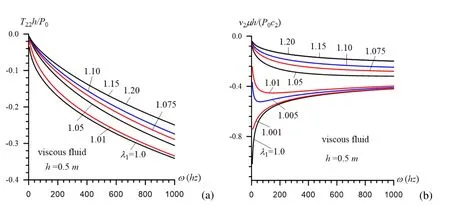
Figure 10:The influence of the initial stretching of the plate on the frequency response of T22(a)and v2(b)in the “thick plate case”under h=0.5m.

Thus,with the above,we restrict ourselves to consideration of the numerical results related to the “thin plate case”.Now we consider numerical results related to the“thick plate case”,according to which,we assume that 0.05m≤h≤1.0m.First,as above,we assume thatωt=2nπ(n=0,1,2,...)and analyze the graphs given in Fig.7 which illustrate the frequency response ofT22(Fig.7a),v2(Fig.7b)andv1(Fig.7c)underλ1=1.0.Note that under construction these graphs we assume that the fluid is viscous one and the results obtained for theT22andv2in the inviscid fluid case coincide with the corresponding ones shown in Fig.7.However,the results obtained for the velocityv1obtained in the inviscid fluid case,as in the “thin plate case”differ significantly from corresponding ones obtained in the viscous fluid case.Taking these discussions into account below,as in Fig.7,we will analyze numerical results related to the viscous fluid case.Thus,we turn again to the results given in Fig.7 and note that these results are given in the compressible and incompressible fluid cases simultaneously.It follows from the analyses of the graphs illustrated in Fig.7 that the fluid incompressibility causes to increase of the absolute values of the stressT22and of the velocityv2and this influence is more considerable for the velocityv2.The magnitude of the mentioned influence increase monotonically with the thickness of the platehand with the frequency of the external forced vibrationω,in other words with increasing of the values of the parameter Ω1in(41).According to the numerical results obtained for various values of the parameter Ω1,in general,it can be noted that the influence of the compressibility of the fluid on the foregoing results becomes considerable in the cases where Ω1≥0.15.Moreover,it follows from the analyses that as a result of the fluid incompressibility the absolute values of the stressT22and the velocityv2increase for the considered pair of the fluid and plate materials.However,the character of the fluid compressibility on the velocityv1depends on the values of the frequencyω.

As an example for results related to the phase shifting of the studied quantities we consider the dependence amongT22,v2andωt.The graphs of this dependence which are obtained for the various values of the plate thickness underλ1=1.0 are given in Fig.9a(forT22)and Fig.9b(forv2).It follows from Fig.9a that the phase shifting for the stressT22is absent in the “thick plate case”.However,this shifting takes place for the velocityv2in the “thick plate case”and decreases with the plate thickness.

Figure 11:The fragments on the convergence of the numerical results under calculation of the integrals(52).

Now we consider numerical results related to the influence of the initial stretching of the plate on the frequency response of the studied quantities in the“thick plate case”.For this purpose we consider the case whereh=0.5mand analyze the graphs given in Fig.10 a(forT22)and Fig.10 b(forv2).It follows from these graphs that,as in the “thin plate case”,the initial stretching of the plate causes to decrease in the absolute values of the stressT22and velocityv2.Moreover,it follows from the graphs given in Fig.10 b that,the initial stretching of the plate also changes the character of the frequency response of the velocityv2,i.e.in the cases wherethe absolute values of thev2increase,but in the case wheredecrease monotonically with the frequencyω.The results given in Fig.10 also show that theT22andv2approach to a certain limit values with the parameterλ1.For instance,the values of theT22(orv2)obtained in the case whereλ1=1.15 coincide almost with the corresponding values of that obtained in the case whereλ1=1.20.

Now we analyze an example related to the convergence of the numerical results with respect toandin the integrals(52).Numerical results obtained for various problem parameters show that the very disadvantaged case in the convergence sense is the “thin plate case”for low frequencies of the external force,namely the case whereh=0.001 and 5hz＜ω≤300.As noted above,under calculation of the related integrals,the interval[0,S∗1]is divided into a certain number of shorter intervals.Let us denote this number throughN.Consequently the length of the mentioned shorter intervals is? and in each of these shorter intervals the integration is made by the use of the Gauss integration algorithm with ten sample point.Consequently,convergence of the mentioned numerical integration can be estimated with respect to the values ofandNfor each fixed value ofAll the numerical results related to the “thin plate case”have been obtained in the case whereand.Some fragments on the convergence of the numerical results obtained for the velocityv2with respect to theandare illustrated in Fig.11.As follows from Fig.11,the noted above selected values of theN,andfor calculation of the numerical results are sufficient in the convergence sense.It should be noted that under the “thick plate case”the convergence of the numerical results is achieved in the relatively small values ofandN.

5 Conclusions

Thus,in the present paper the forced vibration of the system consisting of the prestrained plate-layer and compressible viscous Newtonian fluid has been studied.The motion of the layer is described within the scope of the three-dimensional linearized theory of elastic waves in initially stressed bodies,but the motion of the fluid within the scope of the linearized Navier-Stokes equations.The elastic relations of the plate material are described with the use of the harmonic potential.It is assumed that the velocities and forces are continuous on the interface plane between the fluid and the plate,and two-dimensional(plane-strain state)problem is considered.Also,it is assumed that the forced vibration is caused by the lineal-located time-harmonic forces acting on the free face plane of the plate.The exponential Fourier transformation with respect to the space coordinate directed along the interface is employed for solution of the corresponding boundary-value and contact problem.The inverse of this transformation is found numerically by employing Sommerfeld contour method.Non-dimensional parameters characterized the compressibility and viscosity of the fluid,are introduced and concrete numerical results related to the interface velocities and normal stress are presented and discussed.These results are obtained in the case where the fluid is Glycerin and the values of the elastic constants which enter in the mentioned above harmonic potential and the density of the plate material are taken as Lame’s constants and density of the Plexiglass(Lucite).Consequently,in the case where the initial strains are absent in the plate material the numerical results relate to the hydro-elastic system consisting of the Plexiglass and Glycerin.According to analyzes of these numerical results,it can be made the following concrete results related to the mechanics of the forced vibration of the system under consideration.

·in the“thin plate case”the influence of the fluid viscosity on its flow velocities is significant and must be taken into account under calculation of these quantities;

·the magnitude of the aforementioned influence decreases with the frequency of the forced vibration;

·the compressibility of the fluid on the studied quantities is insignificant in the“thin plate case”;

·the initial stretching of the plate causes a significant decrease in the absolute values of the studied quantities;

·the influence of the fluid viscosity on the fluid velocity in the plate laying direction is not only quantitative,but also qualitative,and this conclusion also occurs for the “thick plate case”;

·the influence of the fluid viscosity on the interface pressure and on the fluid flow velocity in the direction which is perpendicular to the interface plane,is insignificant in the “thick plate case”;

·the influence of the compressibility of the fluid on the values of the considered quantities is significant in the “thick plate case”;

·The existence of the fluid constituents in the system under consideration causes to appear the phase shifting of the studied velocities and stress with respect to the phase of the external forces and the magnitude of this phase shifting decrease with the plate thickness and increase with the initial stretching of the plate.

Akbarov,S.D.(2006a):The influence of the third order elastic constants on the dynamical interface stress field in a half-space covered with a pre-stretched layer.International Journal of Non-Linear Mechanics,vol.41,pp.417-425.

Akbarov,S.D.(2006b):Dynamical(time-harmonic)axisymmetric interface stress field in the finite pre-strained half-space covered with the finite pre-stretched layer.International Journal of Engineering Sciences,vol.44,pp.93-112.

Akbarov,S.D.(2013a):On the axisymmetric time-harmonic Lamb’s problem for a system comprising a half-space and a covering layer with finite initial strains.CMES:Computer Modeling in Engineering&Science,vol.95,no.3,pp.173-205.

Akbarov,S.D.(2013b):Flexural waves in finitely pre-strained solid and circular cylinders made of compressible materials.CMES:Computer Modeling in Engineering&Science,vol.92,no.4,pp.387-421.

Akbarov,S.D.;Guler,C.(2007):On the stress field in a half-plane covered by the pre-stretched layer under the action of arbitrary linearly located time-harmonic forces.Applied Mathematical Modelling,vol.31,pp.2375-2390.

Akbarov,S.D.;Hazar,E.;Eröz,M.(2013):Forced vibration of the pre-stressed and imperfectly bonded bi-layered plate strip resting on a rigid foundation.CMC:Computers,Materials&Continua,vol.36,no.1,pp.23-48.

Akbarov,S.D.;Ilhan,N.(2009):Dynamics of a system comprising an orthotropic layer and pre-stressed orthotropic half-plane under the action of an oscillating moving load.International Journal of Solids and Structures,vol.46,pp.3873-3881.

Akbarov,S.D.;Ilhan,N.(2010):Time-harmonic dynamical stress field in a system comprising a pre-stressed orthotropic layer and pre-stressed orthotropic halfplane.Archive of Applied Mechanics,vol.80,pp.1271-1286.

Akbarov,S.D.;Ilhan,N.(2013):Time harmonic Lamb’s problem for a system comprising a piezoelectric layer and piezoelectric half-plane.Journal of Sound and Vibration,vol.332,pp.5375-5392.

Akbarov,S.D.;Emiroglu,I.;Tasci,F.(2005):The Lamb’s problem for a halfspace covered with the pre-stretched layer.International Journal of Mechanical Sciences,vol.47,pp.1326-1349.

Bagno,A.M.;Guz,A.N.;Shchuruk,G.I.(1994):Influence of fluid viscosity on waves in an initially deformed compressible elastic layer interacting with a fluid medium.International Applied Mechanics,vol.30,issue 9,pp.643-649.

Bagno,A.M.;Guz,A.N.(1997):Elastic waves in prestressed bodies interacting with fluid(Survey).International Applied Mechanics,vol.33,issue 6,pp.435-465.

Biot,M.A.(1965):Mechanics of incremental deformations.Wiley,New York.

Charman,C.J.;Sorokin,S.V.(2005):The forced vibration of an elastic plate under significant fluid loading.Journal of Sound and Vibration,vol.281,pp.719-741.

Emiroglu,I.;Tasci,F.;Akbarov,S.D.(2009):Dynamical response of two-axially pre-strained system comprising of a covering layer and half space to rectangular time-harmonic forces.CMES:Computer Modeling in Engineering and Science,vol.49,pp.47-68.

Fu,Y.;Price,W.(1987):Interactions between a partially or totally immersed vibrating cantilever plate and surrounding fluid.Journal of Sound and Vibration,vol.118,pp.495-513.

Guz,A.N.(2004):Elastic waves in bodies with initial(residual)stresses.A.C.K.,Kiev(in Russian).

Guz,A.N.(2009):Dynamics of compressible viscous fluid.Cambridge Scientific Publishers.

Jensen,F.B.;Kuperman,W.A.;Porter,M.B.;Schmidt,H.(2011):Computational Ocean Acoustic.Sd.Ed,Springer.

Kwak,H.;Kim,K.(1991):Axisymmetric vibration of circular plates in contact with water.Journal of Sound and Vibration,vol.146,pp.381-216.

Lamb,H.(1904):On the propagation of tremors over the surface of an elastic solid.Phil.Philosophical Transactions of the Royal Society of London,Ser.Avol.203,pp.1-42.

Lamb,H.(1921):Axisymmetric vibration of circular plates in contact with water.Proceeding of the Royal Society(London),vol.A 98,pp.205-216.

Lai-Yu,L.U.;Bi-Xing,Z.;Cheng-Hao,W.(2006):Experimental and inversion studies on Rayleigh wave considering higher modes.Chines Journal of Geophysics,vol.49,issue 4,pp.974-985.

Sorokin,S.V.;Chubinskij,A.V.(2008):On the role of fluid viscosity in wave propagation in elastic plates under heavy fluid loading.Journal of Sound and Vibration,vol.311,pp.1020-1038.

Tsang,L.(1978):Time-harmonic solution of the elastic head wave problem incorporating the influence of Rayleigh poles.Journal of the Acoustical Society of America,vol.65,issue 5,pp.1302-1309.

Truesdell,C.;Noll,W.(1965):The nonlinear field theories of mechanics,in:Flugge(Ed.),Handbook der Physik,vol.III/3,Springer,Berlin,New York.

Tubaldi,E.;Armabili,M.(2013):Vibrations and stability of a periodically supported rectangular plate immersed in axial flow.Journal of Fluids and Structures,vol.39,pp.391-407.

Zhao,J.;Yu,S.(2012):Effect of residual stress on the hydro-elastic vibration on circular diaphragm.World Journal of Mechanics,vol.2,pp.361-368.