An Experimental Study on the Wave-Induced Pore Water Pressure Change and Relative Influencing Factors in the Silty Seabed

LI Anlong, LUO Xiaoqiao, LIN Lin YE Qing and LI Chunyu

1) Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Ocean University of China, Qingdao 266100, P. R. China

2) College of Marine Geosciences, Ocean University of China, Qingdao 266100, P. R. China

3) CNPC Research Institute of Engineering Technology, Tianjin 300451, P. R. China

4) Shengli Xinke Marine Survey and Mapping Co. Ltd., Dongying 257055, P. R. China

An Experimental Study on the Wave-Induced Pore Water Pressure Change and Relative Influencing Factors in the Silty Seabed

LI Anlong1),2),*, LUO Xiaoqiao3), LIN Lin1),2), YE Qing1),2), and LI Chunyu4)

1) Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Ocean University of China, Qingdao 266100, P. R. China

2) College of Marine Geosciences, Ocean University of China, Qingdao 266100, P. R. China

3) CNPC Research Institute of Engineering Technology, Tianjin 300451, P. R. China

4) Shengli Xinke Marine Survey and Mapping Co. Ltd., Dongying 257055, P. R. China

In this study, a flume experiment was designed to investigate the characteristics of wave-induced pore water pressure in the soil of a silty seabed with different clay contents, soil layer buried depths and wave heights respectively. The study showed that water waves propagating over silty seabed can induce significant change of pore water pressure, and the amplitude of pore pressure depends on depth of buried soil layer, clay content and wave height, which are considered as the three influencing factors for pore water pressure change. The pressure will attenuate according to exponential law with increase of soil layer buried depth, and the attenuation being more rapid in those soil layers with higher clay content and greater wave height. The pore pressure in silty seabed increases rapidly in the initial stage of wave action, then decreases gradually to a stable value, depending on the depth of buried soil layer, clay content and wave height. The peak value of pore pressure will increase if clay content or depth of buried soil layer decreases, or wave height increases. The analysis indicated that these soils with 5% clay content and waves with higher wave height produce instability in bed easier, and that the wave energy is mostly dissipated near the surface of soils and 5% clay content in soils can prevent pore pressure from dissipating immediately.

wave action; silty seabed; pore water pressure development; influencing factor

1 Intruduction

Due to mass movement of the submarine sediment under wave action, many offshore structures installed on the loose marine sediments are unsafe. The effect of wave action to the submarine stability was recognized and gradually attracted great attention after Henkel found that waves play an important role in seabed stability in the 1970s (Henkel, 1970). The main cause of pore water pressure produced in soils of submarine slope is that wave action can lead to decrease of effective stress and losing of the strength of soil (Yang et al., 1995). The response of pore pressure under wave action has been studied very well in sandy seabed because of its high permeability and non-cohesive property. The sandy seabed could be simplified with a two-phase medium model with both ideal elastic soil skeleton and the compressibility of pore water, which has been widely adopted by researchers (Wang et al., 2008). Yamamoto et al. (1978) explained the response of sandy seabed under wave action based on Biot consolidation theory when he considered the elastic deformation of porous media, compressibility of the pore fluid and the Darcy flow. Later the dynamic response of the seabed under wave conditions was analyzed according to the porous elasticity theory, with both the semi-analytic solution and analytical solution obtained (Jeng and Lee, 2001; Zhang et al., 2012; Zhou et al., 2011). Ulker et al. (2009) concluded that the response depends on the characteristics of the wave and the properties of the seabed after they developed a set of generalized analytical solutions for the response of a saturated porous seabed under plane strain condition. Corvaro et al. (2010) found that the attenuation of the wave action increases with the permeable bed thickness and there is a maximum of wave dissipation in the porous seabed with a depth equal to 2.0–2.5 times the wavelength. But the distribution of silt is extensive over the worldwide submarine bottom, and its engineering properties are different from sand and clay soil, so there are quite a number of differences between silty seabed and sandy seabed under wave action. Tzang (1998) found that pore pressure response of sandy seabed to soil-layer-buried depth differs from that of silty seabed. Wu and Lou (2002) calculated the pore water pressure and effective stress changes of the silty seabed underwave action according to Biot theory and the finite element method. Lin (2001) utilized numerical simulation to study the growth pattern of the pore water pressure of silt under wave action. Feng et al. (2002) used dynamic triaxial test to investigate the silt pore pressure response under dynamic loading. The disintegration may occur when silt meets water except for the case with enough viscosity. It is impossible to consider simply silt as elastic medium or viscous medium. So the silty seabed can not be understood well in the present study. The present mode of pore pressure response to wave action in silty seabed is mostly based on the results of triaxial test or numerical simulation. The triaxial test conditions and boundary conditions of the numerical simulation are very different from factual case. However, the wave flume experiment can produce the same processes. In this paper the pore pressure response of silty bed under wave action was simulated in the flume with considering wave feature and seabed properties. It is very significant in evaluating the stability of silty bed under wave action and understanding the submarine geological process.

2 Experimental Method

2.1 Experimental Equipment and Materials

The wave flume experiment was completed in the Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, the Ocean University of China. The flume with length of 8.9 m, width of 40 cm, and height of 60 cm was used in the experiment. The test area filled with silt with thickness of 50 cm, width of 30 cm and height of 26 cm was located in the rear of the flume, and pore pressure sensors were installed at different depths of the test area (Fig.1).The wave height and pore water pressure were measured by the YY-3 model ultra-compact pressure sensor with sensitivity of 0.001 kPa, developed by the Nanjing Hydraulic Research Institute.

Fig.1 Wave flume sketch map.

The 4 m contour zone of the Yellow River submerged delta was a seriously damaged area in the bottom bed as reported by Li et al. (2001). In this study, a 1:20 scaling model was selected to simulate the wave height of 0.6 m, 1.2 m and 1.8 m in the 4 m water depth zone of silty bed under wave action, as well as the pore pressure response in soil layer, in order to analyze the destruction mechanism of the seabed.

Muds from the Yellow River Delta tidal flats were mixed to obtain samples with clay contents of 5% and 10%, respectively, by using mud consolidation method. Fig.2 shows the test sample size curve (TEST I for sandy silt, the mean grain size d50=0.07 mm; TEST II for clayey silt, the mean grain size d50=0.041 mm). The sample with thickness more than 5 cm was filled into the test area. It took some waiting time to finish the settlement and consolidation of mud in the water. When the actual density of the seabed sample reached 1.78 cm g-3, the bed was flated; finally water was affused to flume until water depth reached 20 cm. Waves with different periods and wave heights could be obtained by adjusting the frequency of the wave paddle during test and wave height could be measured by the Y3 sensor on the bed surface. The pore water pressure at different depth, in the simulated seabed could be measured by Y1, Y2 and Y4 sensors (Fig.1).

Fig.2 Grain size accumulation curve of sample.

2.2 Data Processing

The oscillatory amplitude of the pore pressure caused by wave is defined as wave crest pressure minus wave trough pressure, and it can be directly read from the pore pressure variation curve. It is well known that stability of soil can be influenced by the additional pore pressure caused by the dynamic pressure under wave action, and this pressure is a part of the pore water pressure, as defined as accumulative pore pressure (Jeng et al., 2007). Therefore, pore pressure value of Y1=measured value of Y1-0.3 kPa; Y2 pore pressure value=Y2 measured value-0.8 kPa; Y4 pore pressure value=Y4 measured value-1.5 kPa. Here 0.3 kPa, 0.8 kPa, 1.5 kPa were hydrostatic pressures at 3 cm, 8 cm and 15 cm from bed surface, respectively.

3 Experimental Result

The test wave heights were 3, 6 and 9 cm. The waves with these wave heights were used to simulate ordinary, big and storm waves, respectively, according to wave steepnesses in calculation. Pore pressure response variation with time is shown in Figs.3a–e. The pressure variation in the test bed with clay content of 5% at 3 cm (Y1), 8 cm (Y2) and 15 cm (Y4) distant from bed surface is shown in Figs.3a, c and e, and the variation in the test bed with clay content of 10% is shown in Figs.3b, d and f.

Fig.3 The variation of accumulated pore water pressure with time in bed containing different clay contents (WH is wave heigh).

When test wave height was 3.0 cm, the wave observed was gentle regular sine wave with steepness 0.033. The accumulative pore water pressure gradually rose at sensor Y1 (3 cm soil layer buried depth) before 600 s and then slowly went up. The pore pressure accumulative rate in the bed with 10% clay content was significantly higher than that with 5% clay content, and the accumulative pore pressure reached a stable high value finally. The same result occurred at Y2 (8 cm soil layer buried depth); the pore pressure gradually went up to a higher value and trended to a stable status. The pore pressure accumulative rate in the bed with 10% clay content was obviously higher than that with 5% clay content before 200 s (not 600 s) and its final value was higher too. The pore pressure response at Y4 (15 cm soil layer buried depth) was obviously different from the foregoing cases. The accu-mulative pore pressure changed undulately in the soil with 5% clay content; it rose stably to a certain value and kept stable in the soil with 10% clay content.

When test wave height was 6.0 cm, the wave surface observed was approximately sine wave with steepness 0.075. The accumulative pore pressure gradually rose with time, and then reached a stable value at Y1. Moreover, the clay content had a great influence on the accumulative rate and amplitude of the pore pressure. The accumulative pore pressure reached the highest value in the first 600 s in the soil with 10% clay content; however, the accumulative pore pressure reached the highest value before 1400 s in the soil with 5% clay content. The accumulative pore pressure slightly decreased at the depths of 8 cm (Y2) and 15 cm (Y4) before rising to a stable value, and the rising trend of the pore pressure was identical with that of the pore pressure at Y1.

When test wave height was 9.0 cm, the observed wave steepness reached 0.18. The waves began to break, the wave-surface became very irregular, and the broken waves splashed on the wave flume, the generated waves might be similar to the triangle waves induced by force 6 wind in the sea. The test wave height could reach 9.0 cm occasionally, but most of wave heights were less than 9.0 cm due to the wave breaking. The accumulative pore pressure occurred hardly in the soil with 5% clay content at Y1. But such pore pressure rapidly rose in the first 300 s of wave action on the soil with 10% clay content and then slowly rose afterward at Y1. Similar changes appeared at Y2 and Y4. The accumulative pore pressure gradually rose and reached the highest value before first 300 s of wave action and then slightly decreased to a stable value in the soil with 5% clay content. The accumulative pore pressure kept stable in the first 200 s of wave action and then slightly rose to a stable status in the soil with 10% clay content.

The response of pore pressure to waves had similar features under different wave heights, clay contents and soil depths. It can be inferred that the pore pressure in the silty seabed under wave action showed a rapid rise in the initial period, and then decreased fluctuantly to a stable value in the experiment. The results were obviously different from those of the sandy bed response to the wave action (Luan et al., 2004; Zhang et al., 2012). Therefore, the silty bed can not be considered as a porous elastic medium simply. A reasonable explanation is that the pore water pressure does not dissipate or is transferred at the beginning of the wave action and that the clay of soil to leads an uneven pore pressure distribution, but the upward hydraulic gradient causes pore water to move to surface and results in larger liquefaction potential and breakage of soil structure rapidly, with the pore pressure going up sharply in the beginning of wave action. On the other hand, the existence of a small amount of clay in the silt makes silt produce structure strength and bonding strength, holds back and restrains the increase of pore pressure, and causes the pore water pressure to increase more slowly to a stable value.

The test result indicated that the pore pressure response in silty bed was evident when wave height was 6cm. Therefore, the pore pressure accumulation rate of silty bed under wave action with 6 cm wave height was analyzed, and the variation of pore pressure accumulative rate with depth was also obtained (Fig.4).

Fig.4 The pore pressure accumulative rate versus depth.

Fig.4 shows that the pore pressure accumulative rate was affected by clay content, the rate rising with the clay content increased. That is to say, the rate increased because the increase of clay content reduced the pore pressure dissipation rate.

The above analysis shows that the accumulative rate and amplitude of pore pressure might be affected intensely by the clay content, soil burial depth and wave height. When the bed is acted by wave with the same wave height, pore pressure accumulative rate becomes quicker in the soil with higher clay content; it will reach a higher value at first, then decreases to a stable value. The pore pressure accumulative rate will increase with the wave action time in the silt bed with less clay content, and the final stable value is greater than that in the silt bed with higher clay content. When clay content is 5%, waves with 6 cm wave height most easily make pore pressure to accumulate in bottom of soil layer. The deeper the soil, the higher the pore pressure. The accumulative pore pressure is not obvious in the case of small waves and breaking waves. When clay content reaches 10%, the accumulative pore pressure is independent of wave height.

It can be inferred that the influence of big waves, rather than small waves or breaking waves, on the stability of the seabed at certain depth is most obvious. This role of big waves casuing the destruction of the soil to start from the inside at a certain depth still needs to be proved by more experiments.

4 The Propagation of Wave in the Soil

The propagation of wave in the soil can be illustrated by the amplitude change of oscillatory pore pressure with depth. The waves with wave heights of 3.0, 6.0 and 9.0 cm were used in this experiment. The pore pressure amplitude data were obtained in different soil depth of the silty bed with 5% and 10% clay contents under different wave height conditions (Table 1), and the dynamic pore water pressure amplitude changes with depth are shownin Fig.4. Obviously, in the process of wave propagation, the amplitude of pore water pressure within silty bed was gradually reduced, that is to say, wave energy was attenuated gradually within silty bed. The amplitude attenuation equation, obtained by using regression analysis, can be expressed by exponential law as follows: where A is dynamic pore water pressure amplitude (Pa), m0is dynamic pore water pressure amplitude near the clay surface (Pa), H is wave height (cm), D is soil layer buried depth (cm), R2is correlation coefficient.

The Eqs. (1) and (2) show that the response amplitude of pore pressure in the silty seabed under wave action presents exponential attenuation, which means that the energy of the pore pressure response in the soil under wave action is attenuated according to exponential law. Considering the impact of the dissipative cycle on the pore pressure, the slope of the attenuation curve is related to wave height. The slope of energy attenuation curve is gentle when wave height is lower, but when wave height is higher, energy attenuation slope becomes steep. Obviously, the attenuation of the bigger waves is faster than that of the smaller waves in the silty seabed.

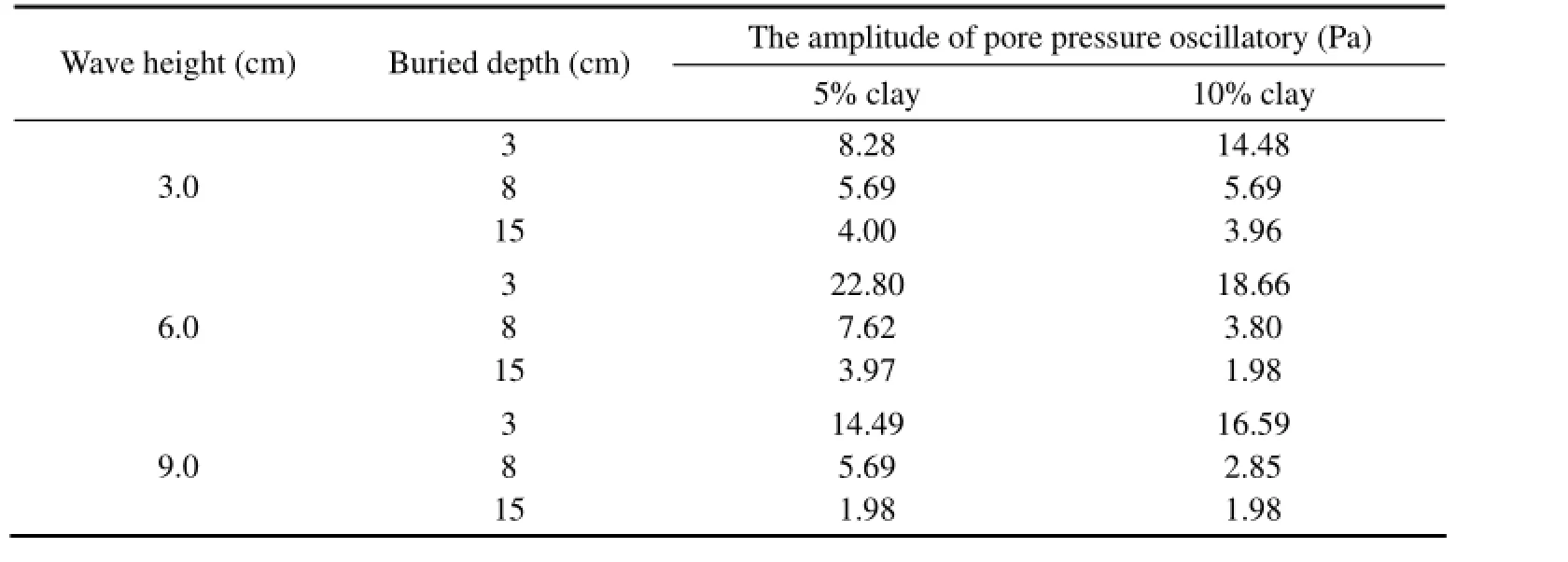
Table 1 The amplitude change of oscillatory pore pressure under wave action in different soil

5 Discussion and Conclusion

In previous studies, people thought that the collapse of seabed bottom suddenly happens during the storm. The two steel platforms overturned in Mexico Gulf and Shengli 3-platform tilted in Bohai Sea are typical examples. The seabed collapse is due to liquefaction induced by suddenly increased pore pressure in the seabed under the action of storm waves (Prior et al., 1986). Our experiment showed that big waves caused higher accumulative pore pressure in the silty seabed before the storm waves came. When the pore pressure reached the critical value, the coming storm waves instantly caused the release of accumulative pore water pressure and the eccentric load of the upper structure, and the seabed was destroyed under big waves and storm. If some techniques to get rid of the accumulative pore pressure are used, the submarine structure foundation failure could be prevented in some liquefaction-sensitive areas before the storm arrives in.

There are many arguments for the silty seabed liquefaction depth problems under wave action. The experiment showed that the energy of wave propagation was attenuated according to an exponential law in soil and the influential depth of the waves was limited. It can be inferred that storm is a factor causing seabed damage.

In this paper, some experimental studies were carried out under wave action. Based on the above analysis, some conclusions are obtained as follows:

1) Accumulative pore water pressure produced under wave action in the silty bed of the Yellow River delta follows the waves appearing or disappearing. Besides, the pressure rises rapidly at the beginning of wave action, and then reduces gradually until being stable. The response model of pressure change in silty bed under wave action differs from that in the sandy bed. The silty bed cannot be simply understood as a porous elastic medium.

2) The amplitude and accumulative rate of the oscillatory pore pressure are related to the soil layer depth, clay content of seabed and loading wave height. Higher soil clay content and greater loading wave height produce lower pore pressure accumulation rate.

3) The energy of wave propagation in the silty seabed will attenuate according to exponential law. The higher the clay content, the faster the attenuation rate. The energy attenuation induced by big waves is faster than thatby small waves in the seabed.

Acknowledgements

The research was financially supported by the National Fundamental Research Program of Ministry of Science & Technology, China (Grant No. 2010CB951202).

Corvaro, S., Mancinelli, A., Brocchini, M., Seta, E., and Lorenzoni, C., 2010. On the wave damping due to a permeable seabed. Coastal Engineering, 57: 1029-1041.

Feng, X. L., Ye, Y. C., Ma, Y. X., and Lin, L., 2002. Silt pore pressure response and dynamic strength under dynamic loading. Journal of Ocean University of Qingdao, 32 (3): 429-433 (in Chinese).

Henkel, D. J., 1970. The role of waves in causing submarine landslides. Geotechnique, 20 (1): 75-80.

Jeng, D. S., and Lee, T. L., 2001. Dynamic response of porous seabed to ocean waves. Computers and Geotechnics, 28: 99-128.

Jeng, D. S., Seymour, B., Gao, F. P., and Wu, Y. X., 2007. The transient and response mechanism of silt seafloor pore water pressure under wave loads. Science in China (Series E: Technological Sciences), 37 (1): 91-98.

Li, A. L., Yang, R. M., Cao, L. H., and Feng, X. L., 2001. The differential erosion and geotechnical properties of the slope soil on the modern Huanghe subaqueous delta. Journal of Ocean University of Qingdao, 31 (3): 435-440 (in Chinese).

Lin, M., 2001. The analysis of silt characteristic under wave loads. Science in China (Series E), 31 (1): 86-96 (in Chinese).

Luan, M. T., Zhang, C. M., Wang, D., and Guo, Y., 2004. Nu merical analysis of residual pore water pressure development and evaluation of liquefaction potential of seabed under wave loading. Journal of Hydraulic Engineering, 2004 (2): 94-100 (in Chinese).

Prior, D. B., Yang, Z. S., Bornhold, B. D., Keller, G. H., Lu, N. Z., Wiseman Jr., W. J., Wright, L. D., and Zhang, J., 1986. Active slope failure, sediment collapse, and silt flows on the modern subaqueous Huanghe (Yellow River) delta. Geo-

Marine Letters, 6 (2): 85-95.

Tzang, S.-Y., 1998. Unfluidized soil responses of a silty seabed to monochromatic waves. Coastal Engineering, 35: 283-301.

Ulker, M. B. C., Rahmana, M. S., and Jeng, D. S., 2009. Wave-induced response of seabed: Various formulations and their applicability. Applied Ocean Research, 31: 12-24.

Wang, Z. T., Luan, M. T., Jeng, D. S., and Liu, Z. G., 2008. Theoretical analysis of random wave-induced seabed response and liquefaction. Rock and Soil Mechanics, 29 (8): 2051-2057.

Wu, M. X., and Lou, Z. G., 2002. Stability and liquefaction analysis of seabed to wave loading. Journal of Engineering Mechanics, 19 (5): 97-102.

Yamamoto, T., Sellmeiher, H. L., and Hijum, E. V., 1978. On the response of a porous elastic bed to water waves. Journal of Fluid Mechanics, 87 (1): 193-206.

Yang, S. L., Shen, W. Q., and Yang, Z. S., 1995. The mechanism analysis of seafloor silt liquefaction under wave loads. Chinese Journal of Geotechnical Engineering, 17 (4): 28-37.

Zhang, J. S., Jeng, D. S., Liu, P. L.-F., Zhang, C., and Zhang, Y., 2012. Response of a porous seabed to water waves over permeable submerged breakwaters with Bragg reflection. Ocean Engineering, 43: 1-12.

Zhou, X. L., Xu, B., Wang, J. H., and Li, Y. L., 2011. An analytical solution for wave-induced seabed response in a multilayered poro-elastic seabed. Ocean Engineering, 38: 119-129.

(Edited by Xie Jun)

(Received April 27, 2013; revised May 13, 2013; accepted March 2, 2014)

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2014

* Corresponding author. Tel: 0086-532-66782076

E-mail: anlongli@ouc.edu.cn