基于服务性能的导航卫星机动时间优化

胡彩波，陈金平，焦玲玲，赵金贤，张之学

(1.武汉大学卫星导航技术研究中心，湖北武汉430079;2.北京卫星导航中心，北京100094;3.天津科技大学电子信息与自动化学院，天津300222)

0 引言

随着航天技术的不断发展，各类型的卫星在轨运行的数量不断增多，据国家无线电监测中心数据显示，截至 2013年 3月，全球共有在轨卫星1 067颗［1］。一方面说明卫星在国民经济、社会发展和军事领域的应用更加广泛，用户对其依赖性增大，对其正常运行的连续性和可用性提出了更高的要求;另一方面，由于空间资源有限，卫星与卫星之间的轨位资源的争夺更加激烈，对卫星轨道控制的策略提出了更高的要求［2］。

近年来，卫星导航系统发展迅速，在轨卫星数量不断增加。导航系统卫星不同于其他卫星，用户对其可用性和连续性有着更加苛刻的要求［3，4］。在轨卫星运行一段时间后，由于受到摄动力的影响，会逐渐偏离轨道。为了保持星座构型，需要对偏离轨道的卫星实施轨道机动。目前的处理策略是在导航卫星进行轨控前，地面控制中心将该星置为“不可用”，提示导航用户不要使用该卫星参与业务处理。这种操作会使用户观测的有效卫星数量减少，导致星座构型发生变化。个别地区和个别时间段出现因星座几何构型变化引起的服务精度下降［5］。下面分析了区域卫星导航系统服务性能的变化规律，提出了一种将轨道机动和系统性能结合的时间选择策略，以降低轨道控制操作对系统服务性能的影响。

1 导航系统服务性能

评价导航系统服务性能的指标主要有精度、完好性、连续性和可用性。精度是指系统为用户所提供的位置和用户真实位置在一定置信概率下的重合度;完好性是指当导航系统的定位误差超过允许限值不能胜任规定的导航工作时，系统能在规定的时间内及时报警的能力;连续性是指假设系统在初始阶段是可用的，其可用性将在运行阶段被保持;可用性是指系统提供可用导航服务的概率［6］。上述4个评价指标是相关的，均与在轨卫星的运行状态有关，在轨卫星“不可用”导致用户可用卫星数量的变化会直接影响到系统的服务性能。

对于卫星导航系统来说，星座的运行是周期性的，可以通过在某一地点、固定间隔内的观测结果来确定星座的可用性。

单点可用性有如下定义:

在位置l，时间t卫星的瞬时可用性为:

式中，bool()X为布尔函数;X为判决条件。

在时刻t0，()t之间，间隔为Δt，共K个时刻的单点瞬时可用性为:

将指定的服务区域按照经纬度格网进行划分，通过计算每一个格网点的单点可用性计算服务区的可用性。

式中，L为服务区域划分的格网点总数;K为间隔为Δt的总的时刻点数;T为统计的总时间;l为计算时所处的位置。

假设各卫星误差相对独立的前提下，用户定位的精度(δ)最终表示为PDOP和伪距误差因子(User Equivalent Range Error，UERE)之积:

对于卫星导航系统，当某颗卫星进行轨道机动时，由于电文参数的计算周期及注入频度限值，卫星播发的轨道参数信息与轨道机动期间的实际运行轨道相比存在差异，用户使用该电文内容进行卫星位置计算时与实际的卫星位置不符，易造成用户计算结果变差。中心控制系统通常将该星置为“不可用”，直至轨道精度恢复至可用范围，再置为“可用”。观测结果显示，这一时间段约6～8 h，且控制比较频繁，地球静止轨道(GEO)卫星20天左右需要进行一次轨道机动控制［7］。

下面重点针对北斗卫星导航系统(BDS)进行分析，空间星座由5颗GEO卫星、4颗中圆地球轨道(MEO)卫星和5颗倾斜地球同步轨道(IGSO)卫星组成［8］，指定分析区域为(55°E ～ 180°E，55°S ～55°N)。BDS卫星全部运行正常时该区域PDOP分布情况如图1所示。

图1 BDS全部卫星可用时平均PDOP

由图1可知，该星座条件下覆盖区PDOP表现为不均匀分布的现象，指定区域的中心区域平均PDOP在2左右，边缘地区平均PDOP可达4以上，这与其GEO+IGSO+MEO混合星座构型是相关的［5］。此星座条件下，每颗卫星都发挥着重要作用，任何卫星“不可用”都会对PDOP产生影响。

2 在轨卫星轨道控制

2.1 轨道控制策略

在轨卫星轨道控制任务包括星座轨道捕获和轨道保持［9］。星座中的每颗卫星由于其初始入轨误差及在轨运行期间所受轨道摄动影响，星座各颗卫星在经过一段时间的运行后会逐渐偏离星座设计的轨道，并逐渐使星座结构失衡，最后导致星座失效，甚至卫星之间发生碰撞。轨道控制的任务就是要保持星座的整体构形。目前轨道控制按照应用方式分为4类:变轨控制和轨道机动、轨道保持、交会和对接以及再入和着陆控制［10］。对于已组网的导航卫星来说，主要是指轨道机动和轨道保持。

轨道控制主要根据在轨卫星运行的轨位，由测控系统发送遥控指令，完成卫星在轨运行位置的调整。对于BDS，是由不同的分系统负责完成导航信息计算与注入、轨道保持与维护等任务，使用的是2套相互独立的设备和数据链路，两者对在轨卫星状态的判读也是相互独立的，轨道控制时机和控制算法等方面有较成熟的理论［2，11，12］。目前的控制策略是以保证卫星安全为主，确保卫星运行在既定的轨道范围。一般通过星上发动机提供的推力实现，也可通过有限推力控制。但不管以何种方式执行，都会使卫星位置发生变化，使卫星播发的导航星历数据精度下降。

2.2 轨道控制对系统服务性能影响

根据导航系统组成、分工和工作原理，运控系统负责导航卫星导航信息的计算和注入以及在轨卫星有效载荷运行状态的监视;测控系统负责卫星轨道保持与控制以及在轨卫星平台运行状态的监视。

运控系统利用监测站观测数据完成在轨卫星的轨道确定，将符合精度要求的定轨结果数据通过上行注入链路注入到卫星，由其按照指定的频度播发给用户。但在卫星轨道控制期间，由于受到电文发播频度及系统体制设计的限制，系统发播的轨道参数精度下降，通常需要将进行轨道控制的卫星标识为“不可用”，以告知用户在卫星轨道机动期间不建议使用该卫星。对于GPS等全球均匀星座来说，在轨卫星数量多且分布均匀，单星“不可用”对服务区内用户服务影响较小［13］;但对于区域卫星导航系统，由于其星座构型的不均匀性，单星“不可用”，将会引起某个地区某段时间星座几何构型的变化，影响到该时间段的服务精度［14］。

针对BDS星座，分析了2013年4月1日至7日的轨道数据，给出指定区域PDOP变化情况，为计算方便，将区域划分成5°×5°的网格，分别计算每个网格点7天内每10 min的PDOP变化情况，并对每个网格点的计算PDOP值求取平均值，找出影响大的卫星和位置。假设一颗卫星进行轨道机动(不可用)，将该星剔除出网络(7天内均不参与处理)，求取与全星座卫星均可用时的差值ΔPDOP(本文仅考虑同一时间只有一颗卫星轨控):

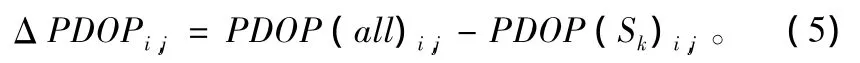
式中，ΔPDOPi，j为网格点i，()j卫星全部正常时PDOP值与卫星k轨控期间 PDOP值的差值;PDOP(all)为卫星全部正常;Sk为卫星k;i为网格点横坐标;j为网格点纵坐标。

针对BDS每颗卫星轨道机动时服务区域内每个格网点PDOP变化情况分别进行统计，求取7天内PDOP变化最大值和平均值，如表1所示。说明每颗卫星置为“不可用”会引起服务区内个别区域PDOP发生80以上的变化，折算到用户端，按照UERE为1 m估算［15］，可产生80 m以上的定位误差。

表1 单星不可用时服务区域PDOP最大差异

3 轨道机动时间优化设计

由表1可知，Sat－5卫星故障时，对服务区域产生的影响最大，下面以Sat－5进行轨道机动为例，分析轨道控制前后服务区内网格点PDOP变化情况。为方便分析，选取图1中变化相对较大且位置不在服务区域边缘的格网点 A(60°E，50°N)，提取该点处Sat－5进行轨道机动前后的PDOP值。

按照目前轨道机动的处置策略，该卫星在可视弧段内的任一时间点均存在实施机动操作的可能。故利用Satellite Tool Kit(STK)软件仿真给出了7天的PDOP变化情况［16］如图2所示(开始时间为2013年3 月13 日 3∶00∶00，每5 min采样)，显示的是Sat-5卫星在7天内任一时间进行轨道机动“不可用”对A点的PDOP影响。由图2可知，PDOP差异表现在个别时间段相对较大。如果错开该影响较大的时段，找到相对变化较小的时间段，进而研究在此时间段实施轨道机动的性能。

图2 A点Sat－5轨道机动与否PDOP变化时间序列

利用卫星广播的基本导航信息，可以得到各颗卫星的位置，计算各点处的PDOP。利用卫星位置的可预报性，设计提出了基于系统服务性能窗口滑动选取轨控时间的方法，以实际获取的卫星轨道作为初始值，参考测控部门给出的计划轨控时间表，计算指定区域和全区域的PDOP变化情况，寻找对全区域或者指定区域影响最小的时间段，反馈给相应的轨道机动实施部门作为参考。

设置表示卫星状态的向量为:

式中，sati表示第i颗卫星的状态，用 bool函数表示。

设置第i颗进行轨控的卫星状态为0:

对指定地区进行PDOP计算，判断指定的轨控时间段内该地区的PDOP变化差值(以该地区该时间段全部卫星可用时计算得到的PDOP为基准)，与门限值进行比较，如果大于门限值，则说明该星“不可用”，对该地区的影响较大，需要调整轨控的时间，按照6 h的窗口(目前轨道机动最短执行时间，可调整)进行滑动，重复比较不同时间段该地区的PDOP差值，选择差值最小即影响最小的时间段，作为该星轨道机动的参考时间，流程图如图3所示。

图3 基于窗口滑动的PDOP计算流程

利用上述方法，结合测控部门给定的卫星轨道机动计划表和指定保障的区域，就可以计算评估该星轨道机动前后PDOP变化情况，通过窗口移动的分析策略，给出较为合理的轨道机动实施时间。针对Sat－5卫星，假设既定轨道机动时间为2013年3月13日9时(图2所示的采样点931处)，可看出A点PDOP由Sat－5星不轨道机动时的7变化为进行轨道机动时的21，如图4所示，影响了该地区服务精度。

图4 A点轨道机动前后的PDOP变化

由图4可以看出，卫星轨道机动对系统服务性能产生一段时间的影响，且卫星轨道机动实际操作也需要一段时间完成，如果将机动时间短暂性的移开，并不能产生对系统服务性能影响最小要求的结果。

针对上述假定轨道机动时间点，运用该处理策略进行分析。设定分析间隔为［－20，20］h，持续时间设定为6 h，窗口滑动步进设定为1 h，计算结果如图5所示。

图5 优化选择轨控时间后的A点PDOP

在测控部门给定的轨道机动时间执行操作是不合适的，如果推迟操作时间，17 h之内对该地区的影响PDOP均＞1;如果提前操作时间，最优值出现在－6 h，如果在该时间实施操作，期间对PDOP变化的影响仅为0.03。

同时也看出，适合轨道机动的时间的选取是依据PDOP变化差异的大小确定的，并不是以找到完全无影响的时间段为最优结果，需综合考虑测控部门的计划窗口以及指定地区服务影响的承受限值，进一步研究PDOP变化的判断阈值。

4 结束语

随着卫星导航应用领域逐步深入，用户对导航系统的依赖性越来越高，要求系统提供连续、稳定和高精度的信号和服务。但对在轨运行卫星进行轨道机动控制也是维持星座构型的必要操作，带来的后果就是卫星一段时间的“不可用”，因而致使用户可视范围内可用卫星数量发生变化。本文基于BDS星座，分析了单颗卫星实施轨道机动对服务区性能的影响，提出了基于计算网格PDOP的窗口式滑动优选卫星轨道机动时间的方法，并进行了7天的仿真分析，确定对指定区域影响最小的时间段，结论可以作为测控系统实施在轨卫星轨道机动的时间选择依据。

［1］赵 爽.全球航天发展情况简介［J］.卫星与网络，2013，7:26 －31.

［2］李恒年，高益军，余培军，等.地球静止轨道共位控制策略研究［J］.宇航学报，2009，30(3):967 －973.

［3］李作虎.卫星导航系统性能监测及评估方法研究［D］.郑州:解放军信息工程大学，2012:140－145.

［4］徐 嘉.故障星分布对星座PDOP可用性影响的建模及评价［J］.航空学报，2008，29(5):1 139－1 143.

［5］陈金平，周建华.卫星导航系统性能要求的概念分析［J］.测控技术，2005，30(1):30 －32.

［6］翟 桅，张国柱.基本星座下北斗卫星导航系统服务性能分析［J］.全球定位系统，2011，4:56 －60.

［7］李国重，李建文，焦文海，等.顾及卫星故障修复的导航星座PDOP可用性分析方法研究［J］.武汉大学学报信息科学版，2010，35(7):841 －845.

［8］北斗卫星导航系统空间信号接口控制文件公开服务信号B1I(1.0版).中国卫星导航系统管理办公室［S］，2012.

［9］蔡成林，李孝辉.混合星座的精度因子与定位性能分析［J］.测绘科学，2009，34(2):67－69.

［10］潘科炎，王旭东，李 果.星座与星座轨道控制［J］.航天控制，2002，3:51 －57.

［11］王 石.卫星轨道控制与轨道确定算法研究［D］.长沙:国防科学技术大学，2002:74－80.

［12］张荣保.卫星轨道保持方法［J］.中国空间科学技术，1988，2(1):48 －50.

［13］WENG Chin － tang，CHEN Chih － wei，TINGET Wen －hing.Statistical Characterization of BEIDOU Navigation Errors with A Consumer Multi Constellation GNSS Receiver［C］∥ION GNSS 2013，2013:2 821 －2 827.

［14］帅 平，曲广吉，陈忠贵.区域导航星座分析设计研究［J］.空间科学学报，2006，26(4):268 －276.

［15］YANG Yuan － xi.Positioning Performance and Contribution of COMPAS［C］∥ ION GNSS+2012，2012:1 728－1 761.

［16］杨 颖，王 琦.STK在计算机仿真中的应用［M］.北京:国防工业出版社，2005:103－123.