含可调参数的保单调有理样条插值

刘永春，王 强，彭丰斌

(安徽理工大学理学院，安徽 淮南 232001)

有理插值在逼近理论中有着重要的作用，Hermite插值是其中典型的方法。然而生成的曲线虽然具有较好的光滑性，但容易产生不必要的震荡，并且有时还会破坏原函数的单调性[1－2］。所以本文详细叙述构造一个分母分子均为二次的分段有理插值函数(即2/2型)的过程，它具有非常好的保单调性并得以验证，而且是含有可调参数的。因为通常的有理插值样条，初始条件一旦确定，曲线的形状也就随之固定了。带有可调参数的有理插值样条，可以通过调整相应子区间上的可调参数，从而对曲线进行局部的调整。用含参数分段有理函数进行插值可解决稳定性和保单调性问题。

1 有理插值函数的构造

1.1 有理插值函数的构造基础

对于f(x)∈C[a，b］，记f(a)=fa，f(b)=fb，f'(a)=d，令b－a=h，作函数

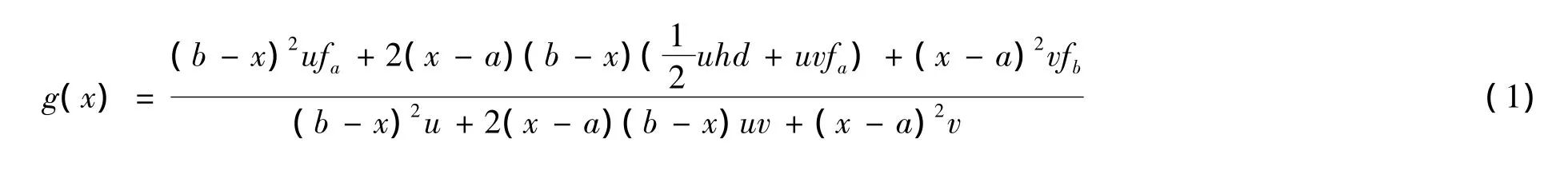
可以验证g(a)=fa，g(b)=fb，g'(a)=d，上述插值函数中的u，v是可调参数，一般地，取u＞0，v＞0。

用给定区间端点的函数值以及其中一个端点上的一阶导数值构造了一个分子分母都是二次的有理插值函数。则对给定区间[a，b］的任意分划a=x0＜x1＜…＜xn=b。若利用上述有理插值函数构造[6］有理插值样条时，只能在两个相邻小区间[xi，xi+1］上以f(xi1)，f(xi)，f(xi+1)，f'(xi－1)，f'(xi+1)插值构造样条函数s(x)，这样就使得s(x)∈C1[a，b］，f(x)∈C1[a，b］，f(a)=fa，f(b)=fb，f'(a)=da，f'(b)=db，b－a=h。若利用上述有理插值函数构造有理插值样条时，只能在两个相邻小区间[xi－1，xi+1］上以f(xi1)，f(xi)，f(xi+1)，f'(xi－1)，f'(xi+1)插值构造样条函数s(x)，这样就使得s(x)在整个区间[a，b］上达不到C1连续。所以，利用区间端点的两个函数值和两个一阶导数值插值，构造分子分母都是二次并且含有可调参数的有理插值函数。

对于函数f(x)∈C1[a，b］，f(a)=fa，f(b)=fb，f'(a)=da，f'(b)=db，b－a=h，仿照式(1)，可将g(x)写成下述形式:

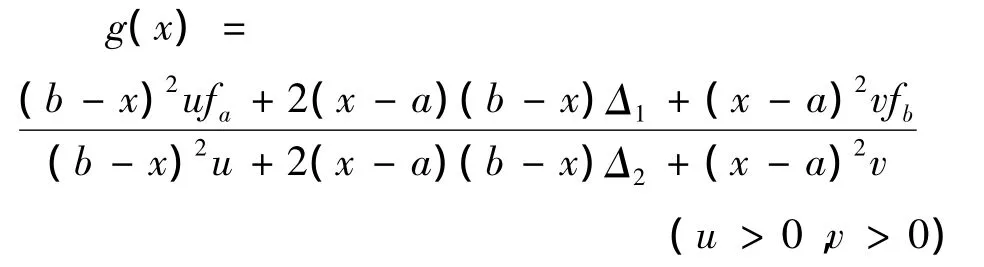
其中Δ1，Δ2是待定的不含x的多项式，由g'(a)=da，g'(b)=db，可得方程组

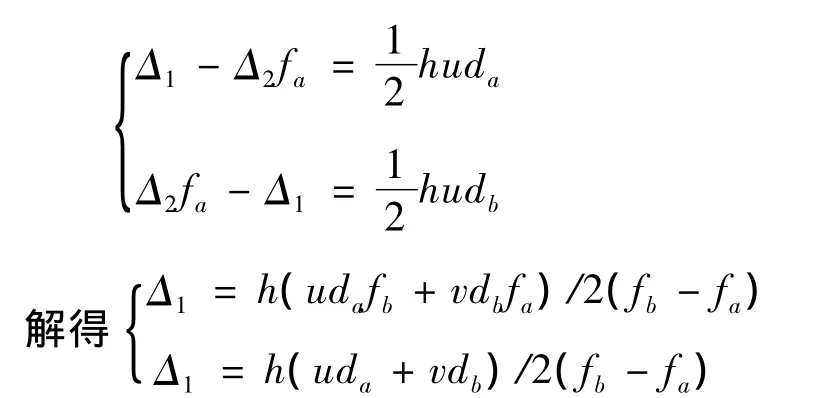
当fa≠fb，即Δ≠0时则得到:

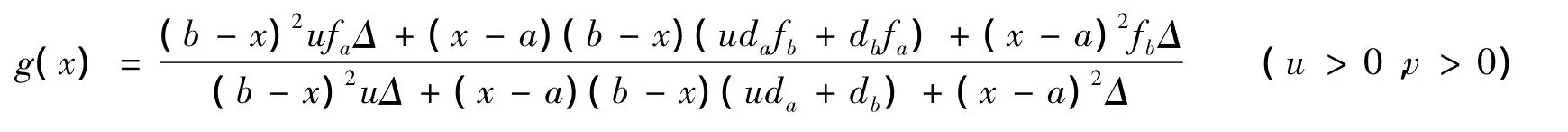
g(x)满足g(a)=fa，g(b)=fb，g'(a)=da，g'(b)=db。因为已经给定了四个插值条件，所以u，v中只有一个是独立的，所以不妨令v=1，得二次有理插值多项式为

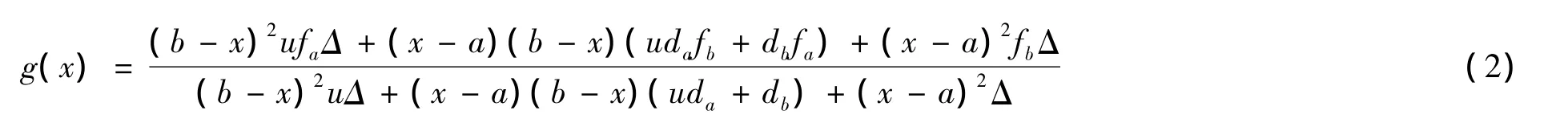
其中u是可调参数，u＞0。

1.2 二次有理插值样条的构造

在区间[a，b］上作分划a=x1＜x2＜…＜xn=b，以f(xt)=fi，f'(xi)=di(i=0，…，n)为插值条件构造有理插值样条s(x)，它在子区间[xi，xi+1］上的表达式为si(x)(i=0，…，n)。si(x)按照式(2)来构造，即x∈[xi，xi+1］，Δi≠0时

Δi=0时

为了将式(3)简单化，不妨令t=(x－xi)/hi，则有如下的插值格式[3－4］。

设f(x)在区间[a，b］上有定义，区间[a，b］剖分为a=x1＜x2＜…＜xn=b。给定数据(xi，fi)，i=1，2，…，n，其中fi为被插函数在分划点xi上的函数值，用di为在给定结点xi处的导数值。记hi=xi+1－xi，Δi=(fi+1－fi)/hi;令t=(x－xi)/hi，当x∈[xi，xi+1］时，定义:

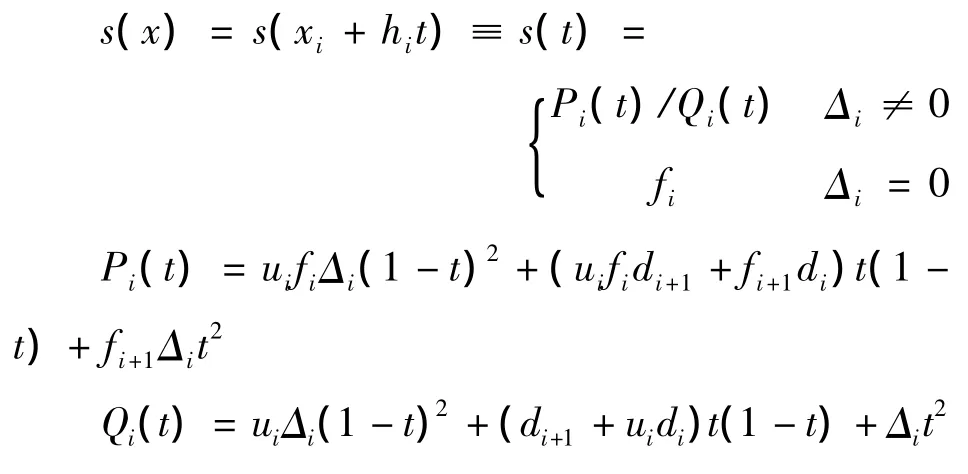
其中ui＞0为区间[xi，xi+1］上的可调参数。

2 插值函数的保单调性

定 理 (保单调性):f(x)∈C[a，b］，s(x)是上述构造的2/2型有理样条插值函数，其中不妨令ui=1，如果f(x)是单调的，则s(x)也是单调的，并且与f(x)的单调性一致。

证明对于x∈[xi，xi+1］，Δi≠0，

s(x)对x求导得:

而其中P'i(t)Qi(t)－Pi(t)Q'i(t)=+2Δit(1－t)+di(1－t)2］

因为导函数值满足保单调的必要条件是

当Δi=0时，di=di+1=0;当Δi≠0时，sgn(di)=sgn(di+1)=sgn(Δi)。

因此s(x)在[a，b］上单调。

3 误差分析

定理1若f(x)∈C1[a，b］，g(x)为由式(2)构造的有理插值函数，则有

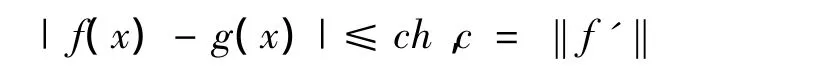
证明因为min{f(a)，f(b)}≤g(x)≤max{f(a)，f(b)}，又由 Lagrange 中值定理，∃ξ1，ξ2，使得

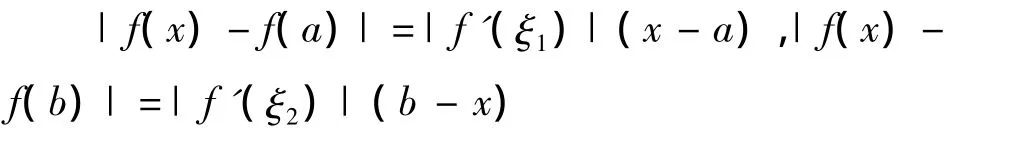
而f(x)∈C1[a，b］，则有

所以|f(x)－g(x)|≤max{|f(x)－f(a)|，|f(x)－f(b)|}≤‖f'‖h=ch，其中c=‖f'‖。

定理2 设f(x)∈C1[a，b］，S(x)是按式(3)定义有理插值样条函数，则

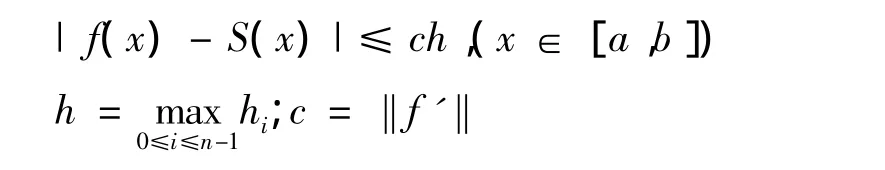
证明当Δi≠0时，由定理1[5］有|f(x)－S(x)|=|f(x)－Si(x)|≤chi，x∈[xi，xi+1］。

当Δi=0时，|f(x)－S(x)|=|f(x)－fi|≤‖f'‖hi=chi，于是在整个区间[a，b］上有|f(x)－S(x)|≤ch，(x∈[a，b］)h==‖f'‖。

给定区间[a，b］，令h=b－a，以f(a)，f(c)，f'(a)，f'(b)为初值按照式(3)插值得到有理样条S0(x)，则由定理2[6－7］有|f(x)－S0(x)|≤ch。

把区间[a，b］等分为[a，c］，[c，b］，以f(a)，f(c)，f(b)，f'(a)，f'(c)，f'(b)为初值按照式(3)插值得到有理样条S1(x)，则由定理2有|f(x)－S1(x)|≤继续对区间[a，c］，[c，b］分别做二等分，…，如此下去，经过n次等分之后，以每个分点处的函数值及一阶导数值为初值，按照式(3)插值得到有理样条Sn(x)，则由定理2有|f(x)－S(x)|≤，可以看到S(x)的逼近阶达到了nn

4 数据实验

下面通过一组单调递减的数据(见表1)和一组单调递增的数据(见表2)分别对2/2型的分段有理插值曲线与二次多项式插值曲线进行了比较[8］，在表1数据下的曲线的比较如图1所示，图2则是在表2数据下的曲线比较。

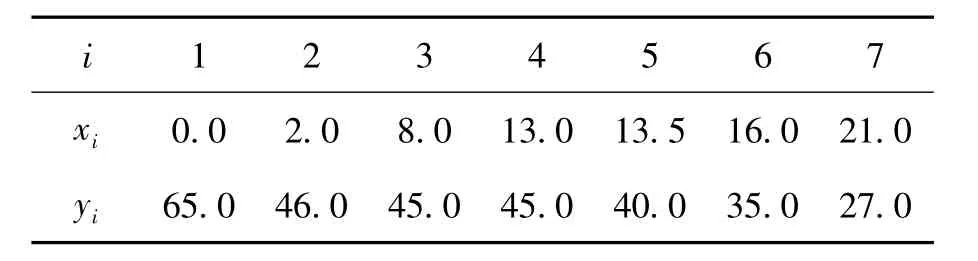
表1 单调递减的数据

图1 数据一下两种插值曲线的比较

表2 单调递增的数据

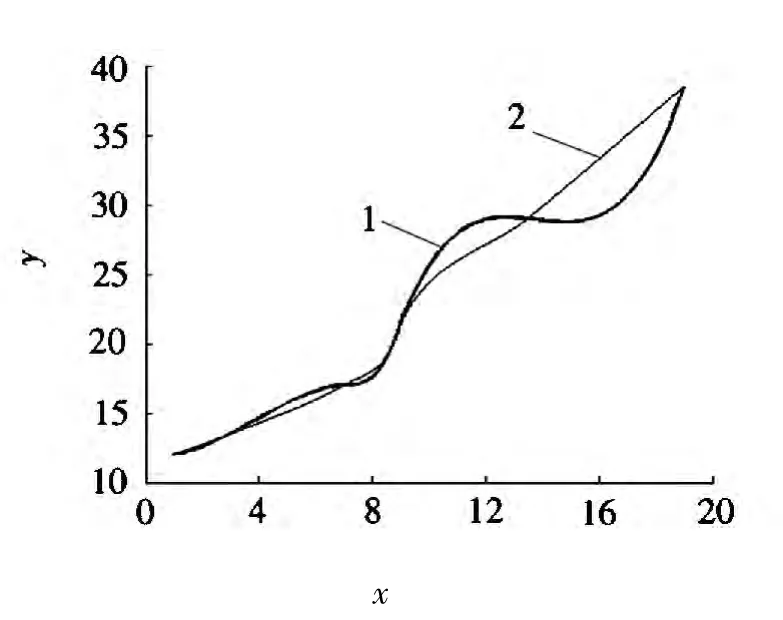
图2 数据二下两种插值曲线的比较

通过图1～图2可知，能明显看出来二次多项式插值曲线虽然有良好的光滑性，但是破坏了原数据单调的性质，并且图1中二次多项式插值曲线有明显的震荡，不稳定。而本文所构造的2/2型的分段有理插值曲线则同原数据有着一致的单调性，并且曲线变化稳定，因此通过数据实验更有力地说明了其稳定性和保单调性的特点。

5 小结

针对Hermite插值的不稳定性，构造了分母分子均为二次的分段有理插值函数(即2/2型)，数值实验验证了此有理插值的保单调性，而且适当地调节可调参数，可以达到曲线的保形性。不过此插值却不能达到C1连续，若为了解决此问题，可以在Δi=0的区间上，按照Hermite插值供述构造Si(x)，但是后者所定义的S(x)却会失去了保单调性。所以，本文所构造的插值还有许多不足，需要继续改进。

[1]虞旦盛，周颂平．有理逼近的一些最新进展[J］．数学进展，2005，34(3):269 －280．

[2]王仁宏，朱功勤．有理函数逼近及其应用[M］．北京:科学出版社，2004:56－70．

[3]王强．三次保形有理插值[J］．合肥工业大学学报:自然科学版，2005，28(11):1 461 －1 464．

[4]田萌．一类保正的有理三次插值样条[J］．山东理工大学学报:自然科学版，2006，20(3):16 －18．

[5]N MACON，D E DUPREE．Existence and Uniqueness of Interpolaiting Rational Functions[J］．The Amer．math．Monthly，1962，69:751 －759．

[6]GREGORY J A，DELBOURGO R．Piecewise rational quadratic interpolation to monotonic data[J］．IMA Journal of Numerical Analysis，1982，2(2):123 －130．

[7]SARFRAZm，AL－MULHEMm，ASHRAF F．Preserving monotonic shape of the data using piecewise rational cubic functions[J］．Computers ＆ Graphics，1997，21(1):5－14．

[8]王能超．计算方法——算法设计及其MATLAB实现[M］．武汉:华中科技大学出版社，2010:45－50．

[9]J A GREGORY．Shape Preserving Rational Spline Interpolation[J］．Rational Approximation and Interpolation，1984，1105:431 －441．