复变量法求解拓扑优化敏度分析研究
龙清平, 杜义贤, 卓道锋
(1.三峡大学机械与动力学院,湖北宜昌443002;2.湖北省水力机械设计与维护重点实验室,湖北宜昌443002)
复变量法求解拓扑优化敏度分析研究
龙清平1,2, 杜义贤1,2, 卓道锋1,2
(1.三峡大学机械与动力学院,湖北宜昌443002;2.湖北省水力机械设计与维护重点实验室,湖北宜昌443002)
研究复变量法对拓扑优化问题敏度分析的有效性和可行性,在现有的经典理论为基础,通过使用无网格伽辽金法离散问题域而求得结构场位移为例,使用O.Sigmund的经典拓扑优化方法,利用复变量来求解出目标函数的导数,然后比较复变量法和直接法某些点敏度分析的误差以及最后拓扑图形的异同,结果显示复变量法和直接法的误差极小,最后通过实际例子结果的总结归纳,能够得出复变量法比较简便易行、精度高的结论。
复变量;拓扑优化;敏度分析;无网格
0 引言
拓扑优化作为一种新兴的结构优化技术,随着相关基础理论和技术的发展,其有很大的发展空间。同时为工程设计和分析人员提供一条新的结构优化技术途径。这种方法自动化程度高,可大大降低工作技术人员的工作量,同时也避免了因多次重复设计所带来的不必要的开支。在工程已经得到大量的应用[1]。
采用优化准则法求解拓扑优化问题时,需要用到目标函数关于设计变量的导数,即目标函数对设计变量的敏度值,灵敏度分析是优化设计的重要内容,它反映的是约束函数和目标函数对设计变量的导数信息,且大型结构的优化设计大部分时间都用在了灵敏度分析。灵敏度分析是研究与分析一个系统或者模型的状态或输出变化对系统参数或周围条件变化的敏感程度的方法[2]。
目前一般有直接法、伴随法和半解析法,这三种方法都要经过公式严格繁琐的推导,才能得出最后的结果。本文通过复变量的方法求解拓扑优化问题的敏度分析,能够直接从目标函数得到其敏度,简单易行。本文将会以密度—刚度插值模型(SIMP模型)为研究对象,通过与直接法敏度分析求导的对比来检测复变量方法的优良性。
1 直接法的敏度分析理论
基于有限元的SIMP模型,我们将构建无网格法的SIMP模型,SIMP模型的表达式:
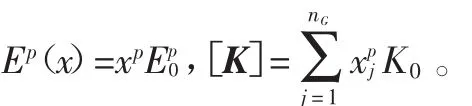
其中,p是中间密度材料的惩罚因子,为了有效压缩中间材料,要求p≥2。Ep表示插值以后的弹性模量,E0为实体材料的弹性模量。参考文献[8],基于有限元法的结构拓扑优化模型,通过无网格伽辽金方法求解位移场的位移,并以结构的柔度最小作为优化目标函数,将SIMP模型离散到高斯点上,我们得出基于无网格伽辽金法的拓扑优
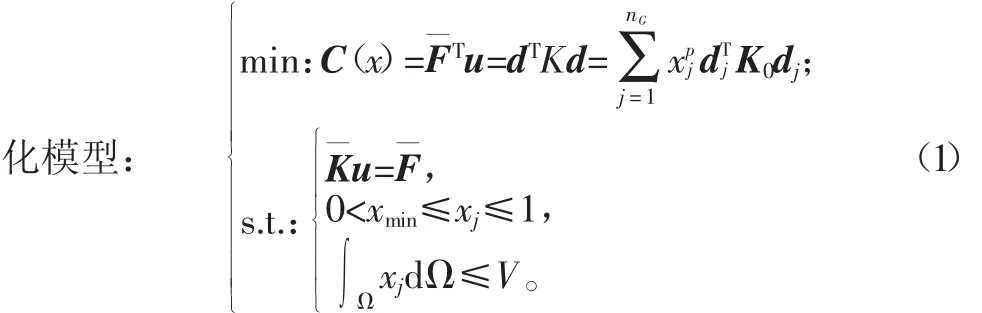
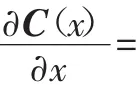
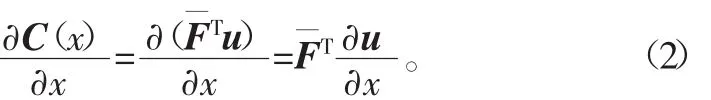
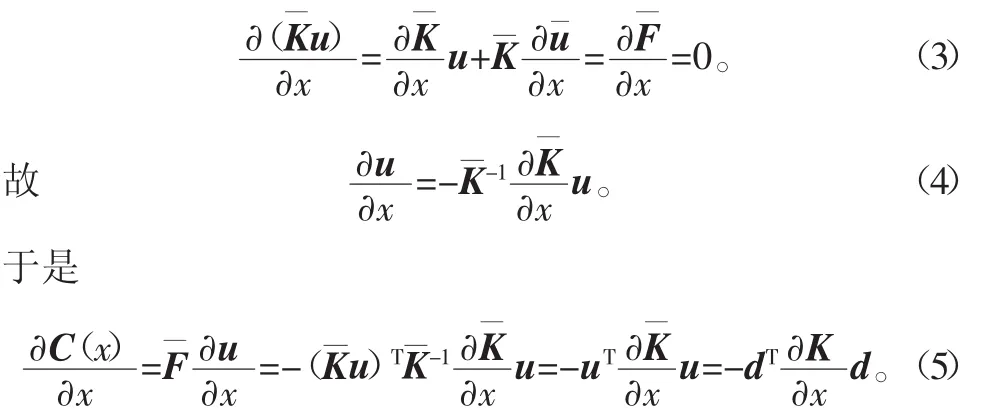
通过式(5)目标函数的敏度公式,可以清楚地看出目标函数的敏度值和位移以及刚度矩阵的关系。
所以,目标函数的敏度具体表达式为
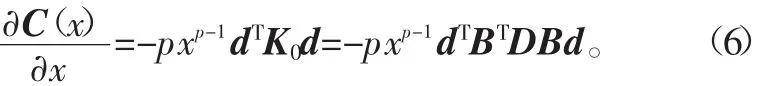
2 复变量法的敏度分析理论
常规的数值求解偏导数的方法是差分法,但是在函数偏导数急剧振荡处或偏导数在较大区间趋于0时,差分法的计算精度较差。为了高精度的数值计算函数偏导数,Lyness等[4]给出了复变量求导法,该方法把偏导数的计算转化为复域函数值的计算,相应的偏导数计算精度很高。近来,郭力等[5]发展了该方法,成功地用于复杂结构的三维边界元计算,并且用于结构优化和参数反演的研究中,本文将复变量法用于拓扑优化的敏度分析中。
根据我们熟知的f(x)在x=x0处的泰勒展开式,对于复数的自变量z=x+hi,其中h是一个标量值,其f(z)在x=0处的泰勒展开式:
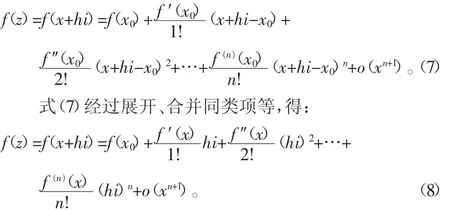
从式(8)我们可以看出,当标量h极小时,一阶导数项要远远大于高阶项,因此通过式(8),我们可以求得其导数。
根据前面实数形式的优化模型,我们将变量变成复数形式,得出基于无网格伽辽金法的优化模型:
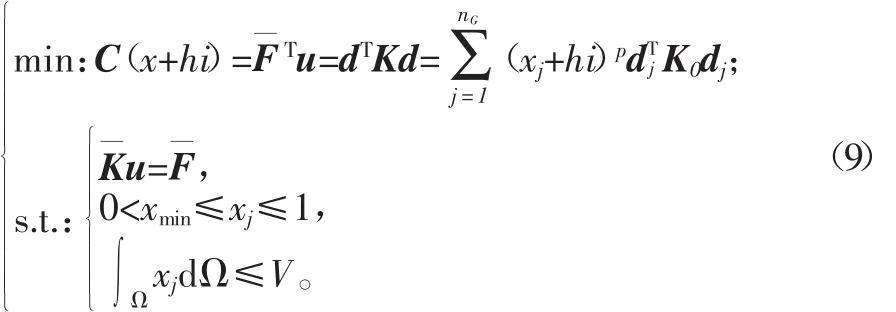
因此式(8)替换函数名称等式依然成立,即

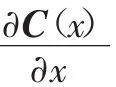
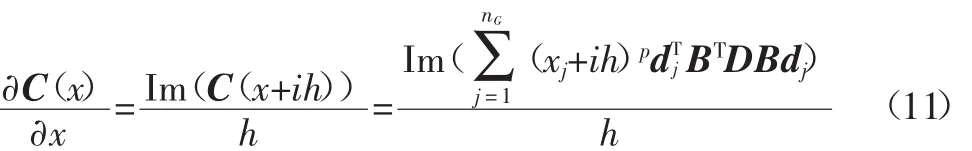
式(11)即为复变量求解的目标函数的敏度具体表达式,通过它可以看出其可以通过目标函数的复变量化一步将其敏度值求解出来。
3 复变量法与直接法对比的数值算例
如图1所示的设计域,长L=2 m,宽D=1 m,左端为固定端,在设计域右边中点加载30 kN的向下载荷。所用材料的杨氏模量为3 GPa,泊松比为0.3,材料的体积约束为40%。采用无网格伽辽金法(EFGM),在设计域上均与布置11×7个节点,根据节点布置将设计域划分为10×6个积分单元,每个积分单元设置4×4个高斯点。
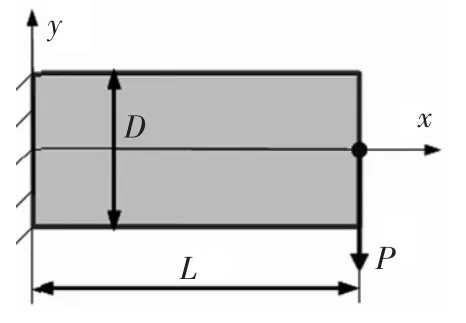
图1 问题域及载荷施加情况
设计变量的控制点A、B、C选取的高斯点依次是第1个、第16×7个、第16×7×11个。
通过以上表1、表2和图2、图3、图4的分析,选取的三个点处,在第7、第18步迭代的敏度误差值非常小,误差数量级为 10-15,在图2、图3、图4中可以看出三个点随迭代步的变化,直接法和复变量法的敏度值变化非常接近。直接法和复变量法对目标函数的求导产生的敏度值,二者之间误差的平均值和方差最大值为第一步迭代的平均值和方差值为5.315E-17和4.623E-32,从而说明复变量求导法敏度的可行性。
通过表3的分析可以看出,在不同的体积约束的情况下,复变量法和直接法求敏度分析后的拓扑图形几乎完全,同时通过对相同体积约束情况下迭代步数以及最后迭代的收敛值情况的比较,说明复变量法求解拓扑优化中敏度问题能够产生直接法相同的效果,从而验证复变量法敏度求导的有效性。
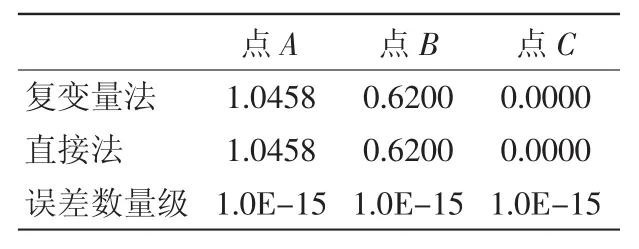
表1 第7步迭代复变量法和直接法的敏度及误差
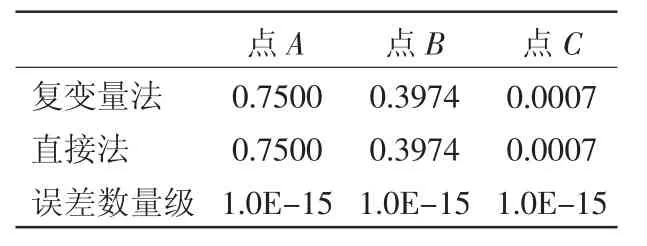
表2 第18步迭代复变量法和直接法的敏度及误差
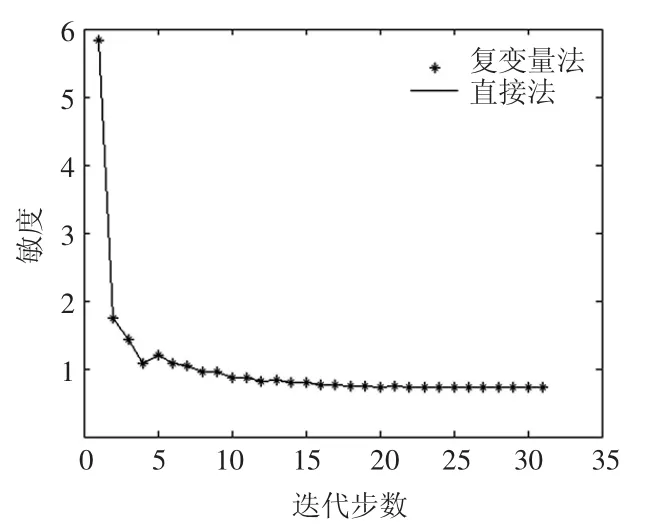
图2 点A处敏度随迭代步的变化
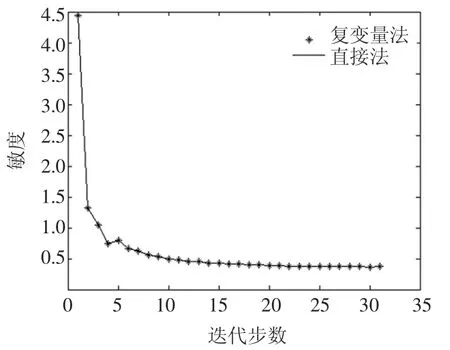
图3 点B处敏度随迭代步的变化
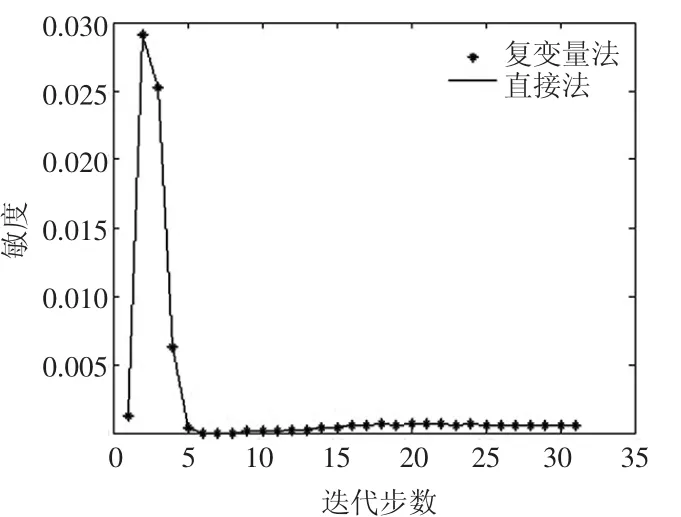
图4 点C处敏度随迭代步的变化
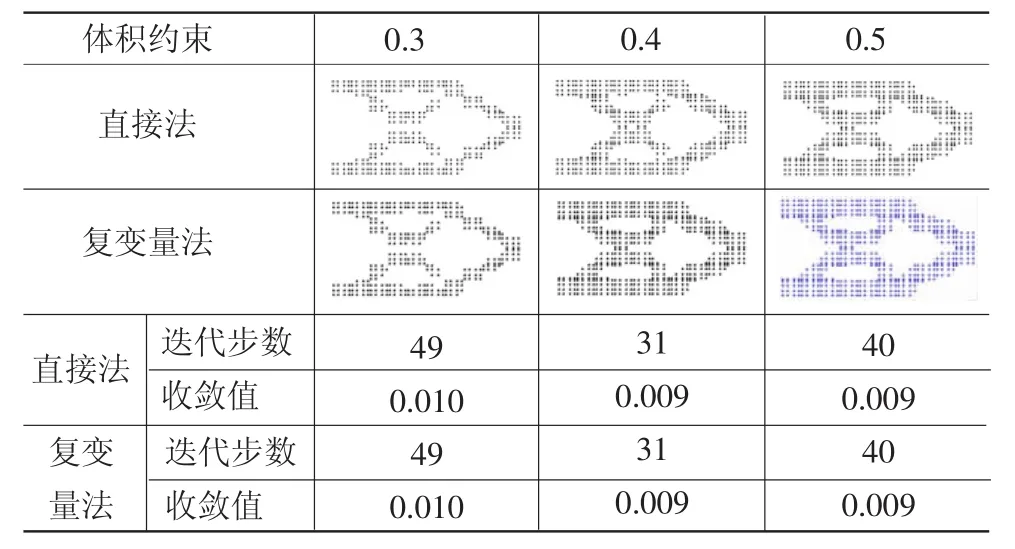
表3 在不同体积约束的情况下直接法和复变量法的比较
4 结论
本文研究了复变量法求解拓扑优化中问题中的目标函数的敏度,通过比较复变量法和直接法的异同,得出了复变量法求解拓扑优化敏度问题是可行和有效的,同时可以看出复变量法对于拓扑优化敏度分析来说简单易懂且精度高,同时易于计算机程序的实现,特别是在多场耦合等情况下,目标函数比较复杂,求导非常麻烦,复变量法求敏度为其提供了一种简单易行的方法。
[1] 李冬梅.多场耦合及多相材料的柔顺机构拓扑优化研究[D].广州:华南理工大学,2011:34-62.
[2] 顾元宪,刘涛,亢战,等.热结构瞬态响应的耦合灵敏度分析方法与优化设计[J].力学学报,2004,36(1):1-4.
[3] 杜义贤.基于无网格柔性机构拓扑优化方法研究[D].武汉:华中科技大学,2007:60-87.
[4] Lyness J N,Moler C B.Numerical differentiation of analytic functions[J].SIAM Journal of Numerical Analysis,1967,4(2):202-210.
[5] 郭力,高效伟.复变量求导法灵敏分析及弹塑性参数反演[J].东南大学学报,2008,38(1):1-4.
[6] 郑娟.基于无网格数值技术的连续结构拓扑优化方法研究[D].长沙:湖南大学,2011:72-98.
[7] 刘翔,龚曙光,曹素,等.EFG法在拓扑优化中的灵敏度分析与应用[J].中国科技论文在线,2008,3(8):553-557.
[8] Sigmund O.A 99 line topology optimization code written in Matlab[J].Struct Multidisc Optim,2001,21:120-127.
(编辑黄 荻)
Sensitivity Analysis of Topology Optimization Based on Complex Variable Method
LONG Qingping1,2, DU Yixian1,2, ZHUO Daofeng1,2
(1.College of Mechanical&Material Engineering,China Three Gorges University,Yichang 443002,China; 2.Hubei Key Laboratory of Hydroelectric Machinery Design&Maintenance,Yichang 443002,China)
The effectiveness and feasibility of complex variable method is studied for sensitivity analysis in topology optimization problem.Based on the existing classical theory,EFGM discrete displacement field of structure is solved using the complex variable out of the derivative of the objective function and O.Sigmund classical topology optimization method.Then the error of the topology graph,sensitivity analysis error of the complex variable and direct method,are compared.The comparison of theoretical and practical examples proves that the complex variable method is more simple and more precise.
complex variable;topology optimization;sensitivity analysis;meshless
TH 122
A
1002-2333(2014)05-0102-03
国家自然科学基金项目(51105229)
龙清平(1987—),男,硕士研究生,研究方向为流固耦合拓扑优化;杜义贤(1978—),男,副教授,研究方向为拓扑优化。
杜义贤,duyixian@aliyun.com。
2014-04-10

