三分谢尔宾斯基垫片上的标准拉普拉斯算子
王 丽
(湖州职业技术学院,浙江 湖州 313000)
0 引言
首先回顾一下三分谢尔宾斯基垫片(SG3)。把一个正三角形看作K0(包括三个顶点p1,p2,p3),三等分三条边可得到九个小正三角形,去掉中间三个。这样重复做下去,最后得到的“极限集”就是三分谢尔宾斯基垫片。
分形集可以通过构造迭代函数系[1]而得到。SG3就可以用由六个部分组成的迭代函数系得到,每一部分都和整体相似,压缩比为这六个相似压缩映射如下
这里x,y∈R。如图1。用K来表示SG3,K就是自相似集[2],那么
下面是本文中的一些符号:
①Vm是m-层上所有顶点的集合,m≥0;
②LA(V0)[2]是V0上所有拉普拉斯算子的集合;
③[Hm+1]Vm是指 Hm+1在 Vm上的限制;
④DF(Vm)[2]是Vm上所有狄利克雷型的集合;
⑤l(Vm)={f:Vm→R},m≥0;
⑥Гm={Vm,Em},这里Em是m-层上所有的边的集合,m≥0;
⑦x~ym意思是:x和y是在一个m-单元的两个点,它们由一条边连接在一起,m≥0;

图1 K0,K1和 SG3
1 三分谢尔宾斯基垫片的调和结构
在这一部分中,我们构造一个{Vm}m≥0上的r-网“自相似”相容序列((Vm,Hm)[2]。用如下方阵来定义三分谢尔宾斯基垫片上最初的拉普拉斯算子D,D∈LA(V0),V0={p1,p2,p3}。

对任意初始D∈LA(V0),我们都能找到一个自相似拉普拉斯算子序列Hm∈LA(Vm),定义如下:
定义1[2](相容序列):设 Vm是一有限集,且对任意 m≥0有 Hm∈LA(Vm)。(Vm,Hm)≤(Vm+1,Hm+1)当且仅当Vm⊆Vm+1和[Hm+1]Vm=Hm成立,那么对所有 m≥0 有(Vm,Hm)≤(Vm+1,Hm+1),这时{(Vm,Hm)}m≥0称为一个相容序列。
定义2[2](调和结构):当且仅当{(Vm,Hm)}m≥0是 r- 网的一个相容序列时是一个调和结构。而且,当对所有i∈S有0<ri<1时,调和结构)称为是正则的。
性质1:若D∈LA(V0),且,对所有 i∈S 有 ri>0,由下式来定义ε(m)∈DF(Vm)。

这里 u,v∈l(Vm),w=w1w2…wm∈Wm,有 rw=rw1…rwm,且 εD= ε0,还有 Hm∈LA(Vm)。记 ε(m)= εHm。
定义εm= ε(m),这里 εm是图能[4]。
而且 ε(m+1)(u,v)
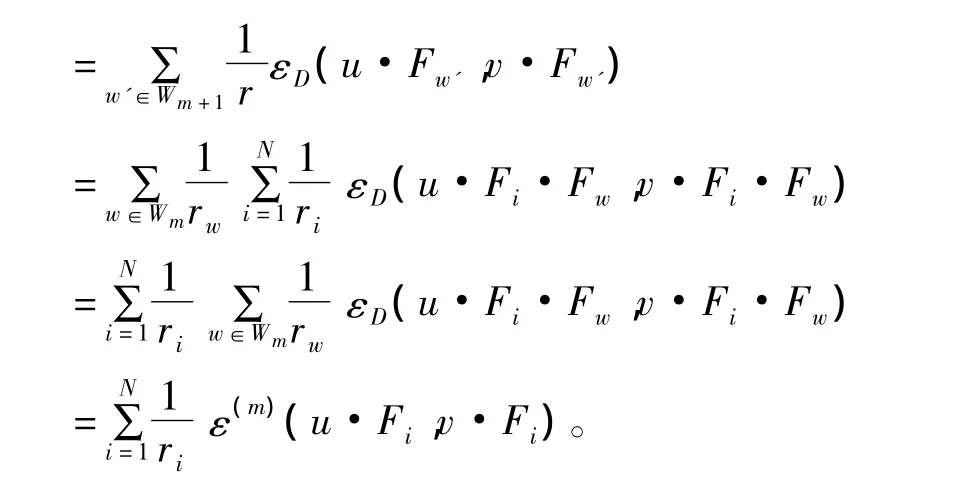
因此,有
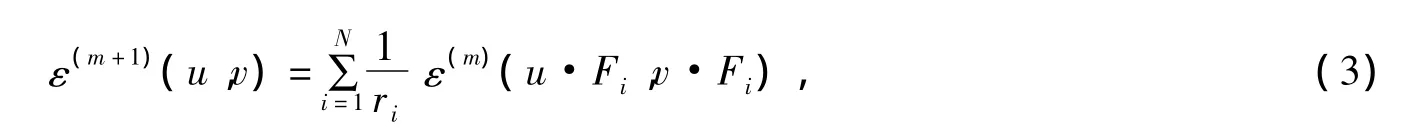
这里u,v∈l(Vm),我们让ε是图能εm的极限。
定理1:对w∈Wm,由Rwf=f·Fw来定义Rw:l(Vm)→l(V0)。那么对所有m≥0,有

证明:注意到 εHm(u,v)是一个内积,因此由内积定义有 εHm(u,v)= -uTHmv,又由(1)ε(m)(u,v)

这里Hm是所有m≥0的Vm上的离散拉普拉斯算子序列。
2 三分谢尔宾斯基垫片上的标准拉普拉斯算子
在这一部分,在自相似空间SG3上通过弱公式化定义拉普拉斯算子△。为了做到这一点需要两个要素:双线性能ε(u,v)[4]和一个正则的概率测度μ[2]。在本文中将μ看作是标准自相似测度,用△μ来表示,它是依赖于测度μ,当μ是标准测度时称△是标准拉普拉斯算子。
定义3[4]设u∈domε且f是连续的。若对所有v∈dom0ε,有下式

那么u∈dom△μ且有△μu=f,(回忆下标0的意思是:v在边界上的取值为0)。
这个定义是弱公式化。接下来将证明有一个与它等价的逐点公式。从下面这个定理来推导逐点公式。
定理2 若h是调和的,那么h∈dom△μ和△μh=0成立。相反,若u∈dom△μ和△μu=0成立,那么u是调和的。
图拉普拉斯算子△m(m≥0)定义在相应的图Γm(它包含顶点和顶点之间的连线)上:

有一个简单的方法从弱公式化得到逐点公式,就是让弱公式化(定义3)中的v=ψ(m)x(注意到:ψ(m)x那么由和 εm(u)=r-mEm(u)(详细看[3]),再综合(6)式,可得中任意变换 x,都有这样式(5)就变成


定理3 设u∈dom△μ,那么逐点公式(8)成立,且极限一致遍及V*V0。相反,假设u是连续函数且(8)式的右边一致收敛到V*V0上的一个连续函数。那么,u∈dom△μ和(8)式成立。
当x∈V0,那么逐点公式就是

这里{xm}是一序列,其中xm∈VmV0且mli→m xm=x。
在 K=SG3中,定义,Vm,x={y∈Vm:y≠x,存在 w∈Wm使得 x,y∈Fw(V0),这里 w=|m|,m≥0},A={x∈Vm:x=Fw(p1)∩Fw(p2)∩Fw(p3)},那么

所以有
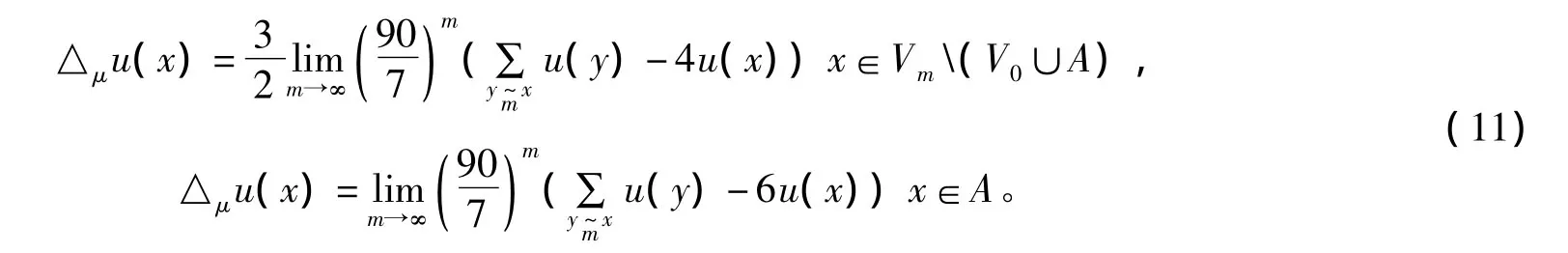
顶点x为任意非边界点,拉普拉斯算子△μ称为三分谢尔宾斯基垫片上的标准拉普拉斯算子。
[1]肯尼思·法尔科内.分形几何中的技巧[M].曾文曲,译.沈阳:东北大学出版社,2005.
[2]Jun Kigami.Analysis on fractals[M].Beijing:Mechanical Industry Press,2004.
[3]FENG Zhi- gang,WANG Li.Harmonic extension on the level-3 Sierpinski Gasket[J].International Journal of Nonliner Science,2010 ,10(3):308 -312.
[4]Robert S.Strichartz.Differential Equations on Fractals[M].New Jersey:Princeton University Press.2006.

