基于支持向量机的东港市降水量预测模型研究

倪远臣

（辽宁省东港市友谊灌区管理处 辽宁 丹东 118300）

近年来，许多学者着眼于降水量的研究，取得了较为可观的结果，其方法层出不穷，基于预测模型的研究深受诸多学者喜爱。滕卫平等（2008）应用SVM回归法对浙江省汛期旱涝灾害进行预测[1]。周振民等（2011）运用BP神经网络对郑州市旱灾进行预测，该模型对预测郑州旱灾发生情况具有重要的参考价值，依据BP神经网络预测模型的预测结果结合郑州市的实际情况提出可靠的防灾、减灾对策[2]。鉴于上述研究，本文将运用支持向量的降水量预测模型，对辽宁省东港市降水量进行预测分析，以期得较好的预测效果，为东港市降水量预测提供一种新的思路。

1 模型的基本原理

1.1 支持向量机的基本原理

支持向量机 （SupportVectorMachines,SVM）由Vapnik在20世纪90年代发明，是统计学理论上一种通用的学习算法，它基于核函数进行学习，具有数据挖掘能力。支持向量机的基本思路是通过非线性映射将输入空间的低维变量变换到一个高维的特征空间中，在这个高维特征空间中进行线性回归，非线性变换。支持向量机方法具有三个主要优点：首先，SVM算法最终将转化成为一个二次型寻优问题，解决了神经网络方法中局部极值问题；其次，针对有限样本情况，其目标是得到现有信息下的最优；第三，支持向量机模型将实际问题通过非线性变换转换到高维的特征空间，在高维空间中构造线性判别函数来实现原空间中的非线性判别函数，同时它巧妙地解决了维数问题。基于上述优点SVM被广泛应用于回归问题（时间序列分析）和模式识别（分类问题、判别分析）并推广到预测和综合评价等领域[3-5]。

其基本原理如下：假定给定的训练样本为（xi,yi）（xi∈Rn为输入变量，yi∈Rn为对应输出值，i=1，2…L，L为样本个数），通过一个非线性映射Φ将数据映射到高维特征空间F，实现将非线性回归问题转化为高维特征空间的线性问题，

其中：b为阀值，w为权值矢量，Φ（x）是将样本点映射到高维空间的非线性变换，f（x）为x的非线性函数，同时又是Φ（x）的线性函数，x和b是通过正则化和结构风险准则来估计的，根据结构风险最小化准则得:

ε为引入的不敏感损失函数，其定义为：

通过利用对偶原理、拉格朗日乘子法以及核函数方法其回归方程最终表达式为：

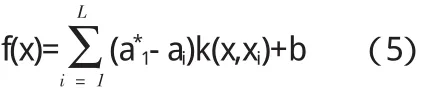
其中：ai*、ai为二次规划中的拉格朗日乘子，常用核函数有线性核函数、多项式核函数、径向基核函数和Sigmoid核函数，本文选用径向基核函数：

其中，k（x,xi）是满足Mercer条件的核函数，其作用是不必知道从低维输入空间到高维特征空间非线性映射的Φ （x）具体形式，通过引入核函数就可得到回归方程。

1.2 BP神经网络的基本原理

BP（Back Propagation Network）人工神经网络是由Rumelhart和Mc Celland为首的科学家小组于1986年提出的，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP神经网络能够学习和存贮大量的输入—输出模式映射关系，具有拓扑结构，包括输入层（input）、隐层 （hidelayer）和输出层（output layer）。由于其具有大规模处理信息、存储信息及良好的自主学习能力等特点，被广泛应用于诸多领域[6-8]。

2 实例应用

2.1 地区概况

图1 东港市降水预测值与真实值对比图

表1 预测模型精度表

东港市地处辽东半岛东端，位于东经123°22′～124°22′，北纬 39°45′～40°15′，隶属于辽宁省丹东市，南临黄海，东依鸭绿江，和朝鲜隔江相望，与日本一衣带水，拥有沿海、沿江、沿边的地理优势，是中国海岸线上最北端的县级市。它是一座新兴沿海港口城市，境内边境线23.85km，海岸线93.5km，全境东西极长83km，南北极宽 38km，陆域面积 2396km2，海域面积3500km2。辖15个乡镇、3个街道办事处、5个国有农场、2个省级经济开发区，总人口64万。东港属温带湿润地区大陆性季风气候，并具有海洋气候特点，四季分明。年平均降雨量786mm，年平均气温8.9℃，有大小河流12条、水库42座，水资源储量为全省平均水平的3倍，城市日供水能力20万t，是环黄渤海著名的丰水城市。东港是东北出海口，素有“北国江南”的美誉，2010年跻身“全国百强县”。

2.2 模型的预测结果与分析

根据辽宁省东港市44年（1970年～2013年）年均降水量通过matlab工具建立基于支持向量机的降水量预测模型、BP神经网络降水预测模型。基于SVM的降水量预测模型、BP神经网络预测模型均选取34年降水量作为训练样本，10年的降水量作为测试样本。支持向量机参数的选择，即不敏感损失函数ε和误差惩罚因子C，ε影响支持向量的数目，ε值越大，支持向量数目就越少，估计的函数精度越低；C取得小，训练误差变大，系统的泛化能力变差，C值大，泛化能力下降，以平均相对误差最小为寻优条件，得到不同序列的最优参数；BP神经网络降水量预测模型选用单一隐层的拓扑结构，输出层神经元传递函数设定为tansig，训练函数设定为trainglm，学习速率初始值为0.1，动量系数的初值设值为1，训练次数为1000次。在模型运行过程中发现，BP神经网络表现出它固有的弊端，即BP神经网络降水量模型需经过多次试错法才能最终确定预测的结果；而SVM支持向量机降水量预测模型表现出较好的自主学习能力、泛化能力，收敛速度快。两种预测模型的预测结果，如图1所示。

选择均方误差（MSE）和确定性系数（R2）作为基于支持向量机的降水预测模型、BP模型预测精度的评价标准。公式如下，模型精度检验结果如表1所示：

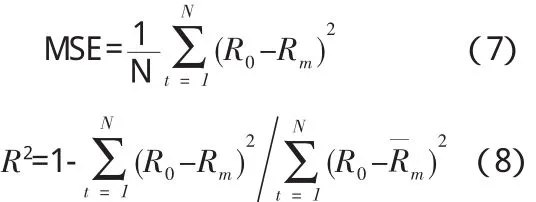
其中：Ro为实际降水值；Rm为预测降水值为实际降水量平均值；

表1结果所示：辽宁省东港市基于支持向量机的降水量预测模型的预测值均方误差（MSE）值小于BP神经网络预测结果，决定系数 （R2）大于BP神经网络预测模型的预测结果。可见，基于SVM的降水量预测模型能够真实的反应东港地区降水量的变化，其预测结果优于基于BP神经网络降水量预测模型，且学习速度快，克服了传统BP神经网络的一些缺点，将支持向量机的降水量预测模型应用到辽宁省丹东市降水量预测中具有一定的可行性。

3 结论

基于支持向量机的降水量预测模型具有结构简单、学习速度快、全局最优、泛化性能好等优点，能较好解决小样本、非线性、高维数和局部极小等问题，克服了传统的神经网络模型所固有的局部极小点、过学习现象以及结构和类型的选择过于依赖经验等缺陷[9]。通过对辽宁省东港市44年的年均降水量的预测研究发现，基于SVM的降水量预测模型可以有效的预测东港市的降水量，且方法简单，获得了较高的预测精度，为东港市降水量变化提供了依据，具有较大的参考价值。陕西水利

[1]藤卫平,俞善贤,胡波等.SVM回归法在汛期旱涝预测中的应用研究.浙江大学学报（理学版）,2008,35（3）:343-347.

[2]周振民,谢滨帆.BP神经网络在郑州市旱灾预测中的应用及防灾减灾对策.中国农村水利水电,2011,12:97.

[3]刘向东,骆斌,陈兆乾.支持向量机最优模型选择的研究[J].计算机研究与发展,2005,42（4）:576一581.

[4]Vapnik著,张学工译.统计学习理论本质[M].北京:清华大学出版社,2000.

[5]刑佳莹,黎奥华,张佳薇.基于粒子群优化支持向量机的时间序列木材含水率预测[J].林业科技,2012,37（1）:24-27.

[6]曹广学,张世泉.2005.BP模型在降雨径流预报中的应用研究.太原理工大学学报,36（3）:350～353

[7]孙吉辉.基于人工神经网络模型的降水量预测研究[D].山东青岛:中国海洋大学,2008.

[8]董长虹.MATLAB神经网络与应用 [M].北京:国防工业出版社,2005.

[9]BURGES C. A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery, 1998,2(2):121-127.