含分布Henstock－Kurzweil积分的一阶反周期边值问题

周 浩，叶国菊，王 鸥，杨慧敏

（河海大学 理学院，南京210098）

0 引 言

文献［1－6］在反周期边值条件下，分别研究了常导数意义下一阶常微分方程、高阶微分方程、偏微分方程和抽象微分方程解的存在性.

考虑如下含有分布导数的反周期边值问题：

其中：x′表示x的分布导数；x∈C（［0，T］）；T是正常数；f：ℝn×［0，T］→ℝn为分布（广义函数），满足如下假设条件：

（H1）f（·，t）连续，对∀t∈［0，T］成立；

（H2）对每个固定的x∈C（［0，T］），f（x（·），·）为DHK可积；

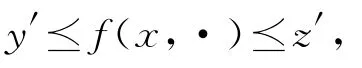
本文先给出分布Henstock－Kurzweil积分的定义及一些性质定理，然后利用Schauder不动点定理证明反周期边值问题（1）解的存在性定理，并举例说明结果的广泛性.

1 预备知识

定义基本空间为

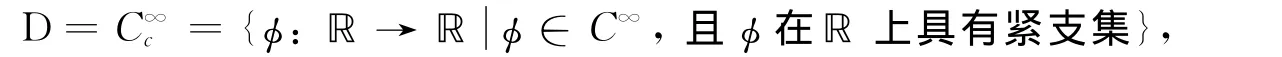
其中φ（x）的支集是使φ（x）≠0全体点集的闭包.序列｛φn｝⊂C∞c收敛到φ⊂C∞c是指：存在紧集K⊂ℝ，使得φ和φn的支集都包含在K 中，且对每个m∈ℝ，序列｛φn｝的各阶导数｛φmn｝在K中一致收敛于φm，其中φ∈D称为检验函数.

D上的连续线性泛函称为分布（或广义函数）.由D上分布全体构成的空间是基本空间D的共轭空间，记作D′.若f∈D′，则f：D→ℝ，记作〈f，φ〉∈ℝ，其中φ∈D.

定义分布f∈D′的分布导数f′为〈f′，φ〉＝－〈f，φ′〉，其中φ是检验函数.在这种导数定义下，所有广义函数任意阶均可微，且任意阶导数都是广义函数.

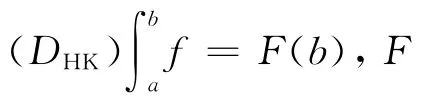
在定义1下，如果f∈DHK，则对任意的φ∈D（（a，b）），满足

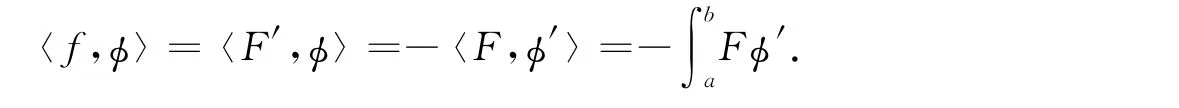
由DHK积分的定义可见，DHK积分是一种更广泛的积分，它包含了Riemann积分、Lebesgue积分和Henstock－Kurzweil积分.

下面举例说明DHK积分的广泛性.

例1［7］如果F是［a，b］上几乎处处逐点可微的连续函数，则F广义绝对连续.进一步，如果函数F在［a，b］上连续但不可微，则F非广义绝对连续.若F在［a，b］上不可微且F∈C（［a，b］），则F′存在且DHK可积，但非 Henstock－Kurzweil可积.反之，如果F广义绝对连续，则F∈C（［a，b］），F′（t）不仅 Henstock－Kurzweil可积而且DHK可积.此时F′（t）是F（t）的常导数.

在DHK空间中，若定义范数‖f‖＝‖F‖∞，其中F∈BC是f的原函数，则DHK是Banach空间.

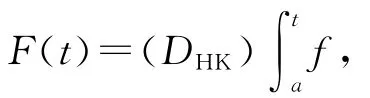
在DHK空间中，定义偏序如下：若f，g∈DHK，则fg（或gf）当且仅当f－g在［a，b］上是一个正测度.即如果f，g∈DHK，则当fg时，有在这种偏序关系下，以下结论成立.

引理2［8］对于f，g，h∈D′（（a，b）），fgh，若f，h是DHK可积的，则g也是DHK可积的.

如果当n→∞时，有‖fn－f‖→0成立，则称序列｛fn｝⊂DHK强收敛于f∈DHK，记作fn→f.

DHK的共轭空间为有界变差值函数构成的空间BV［10］.

2 主要结果

反周期边值问题（1）可以写成如下形式：

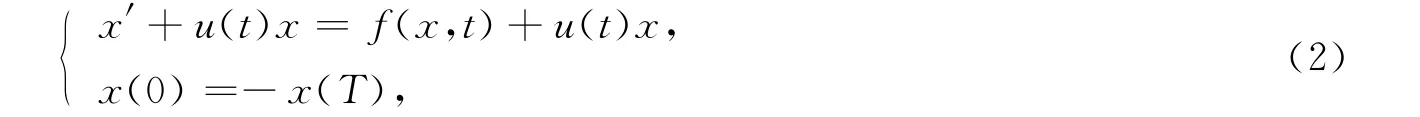
其中：t∈［0，T］；u（t）是［0，T］上的非负、连续有界变差函数.

若g（x，t）＝f（x，t）＋u（t）x，则问题（2）变为

易验证g满足如下假设条件：

（H4）g（·，t）连续，对∀t∈［0，T］成立；

（H5）对每个固定的x∈C（［0，T］），g（x（·），·）为DHK可积；

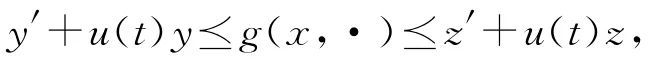
引理5 反周期边值问题（3）与下述积分方程等价：

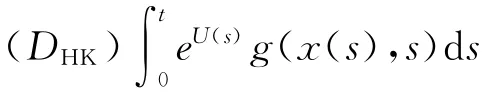
引理6（Schauder不动点定理）［11］设X是Banach空间，集合M是X 中的非空有界闭凸集；算子A：M→M是紧算子，则A有不动点.

定理1 假设条件（H4）～（H6）成立，则反周期边值问题（3）有解.

证明：在［y，z］上定义算子A：

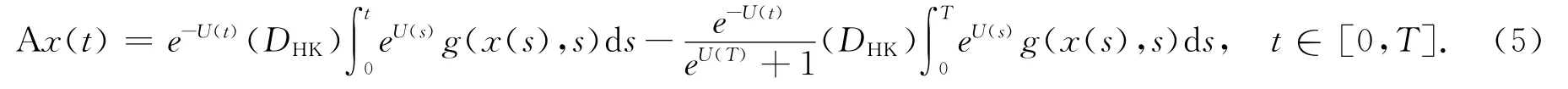
对任意的x∈［y，z］，由式（5）得

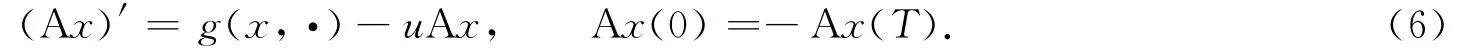
令w＝Az－z，由条件（H4），（H6）和式（5），（6）得

进一步有

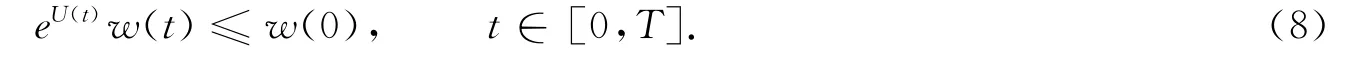
由式（7），（8）可得

通过式（8），（9）得：w＝Az－z≤0，对所有的t∈［0，T］成立，所以Az≤z.同理可得：Ay≥y.因此，A：［y，z］→［y，z］.于是，当x∈［y，z］时，

由（H6）可验证A（［y，z］）在［0，T］上是一致有界的.

要证明A：［y，z］→［y，z］是紧的，需要验证A连续并且A（［y，z］）是相对紧集.

1）A（［y，z］）是相对紧集.

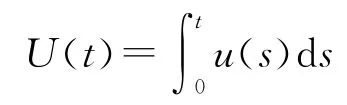
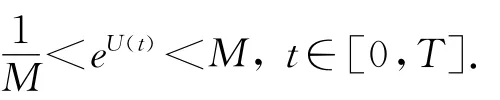
由式（5）得

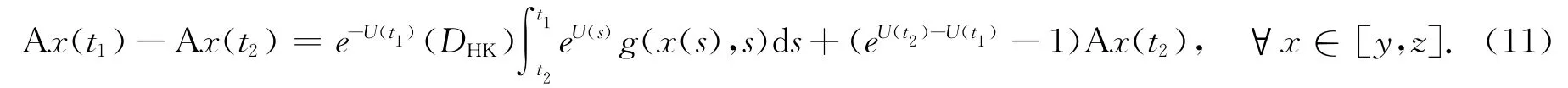
因为对任意的t∈［0，T］，eU（t）g（·，t）是单调的，所以

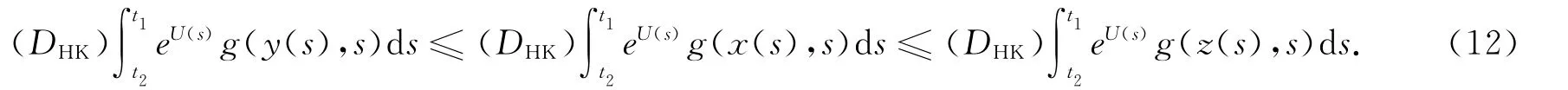
从而存在N＞0，使得

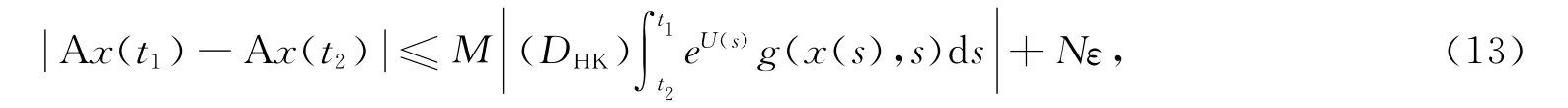
由式（11）～（13）得

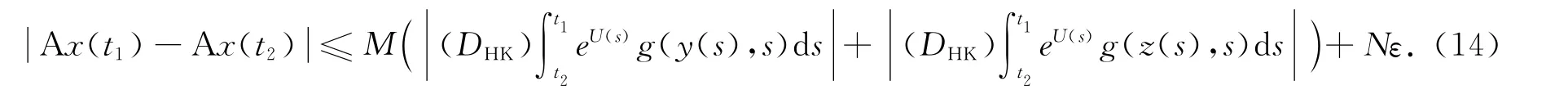
又因为eU（t）g（y（t），t），eU（t）g（z（t），t）关于t∈［0，T］是DHK可积的，所以它们的原函数在［0，T］上连续，也是一致连续的.因此，A（［y，z］）在［0，T］上等度连续，对∀x∈［y，z］成立.由 Ascoli－Arzelà定理知，A（［y，z］）是相对紧集.

2）算子A连续.

假设序列｛xn｝⊆［y，z］，x∈［y，z］，当n→∞时，xn→x.由（H4）知

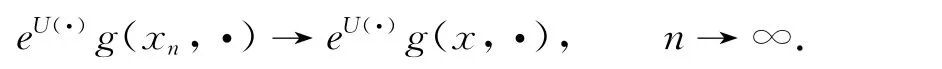
利用式（5）和引理3，有

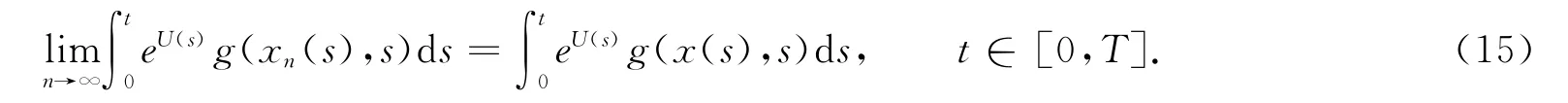
综上所述：算子A满足引理6的条件，故A有不动点.因此反周期边值问题（3）有解.证毕.

由定理1，可得如下结论：

推论1 若反周期边值问题（3）有解，则反周期边值问题（1）也有解.

推论2 假设f：ℝn×［0，T］→ℝn，f（x，t）＝f1（x，t）＋f2（t）.若f1（x，t）满足条件（H1）～（H3），f2（t）在［0，T］上DHK可积，则反周期边值问题（1）有解.

证明：显然，f（x，t）关于x连续，关于t∈［0，T］是DHK可积的，所以f（x，t）满足（H1）～（H3）.由推论1知反周期边值问题（1）有解.

3 应用实例

例2 考虑反周期边值问题：

其中φ（x，t）关于x连续，且

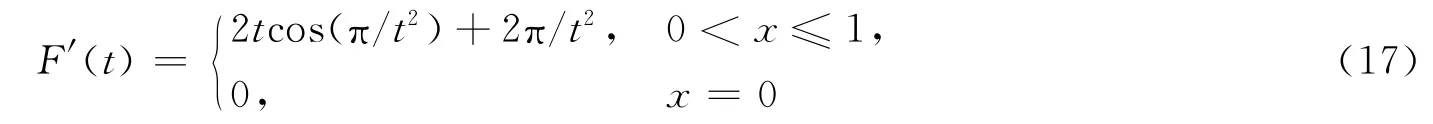
是

的导数.则问题（16）有解.

证明：令f1（x，t）＝t2x＋φ（x，t），f2（t）＝F′（t），则f1（x，t）关于x 连续，f2（t）在［0，1］上Henstock－Kurzweil可积.由推论2知，反周期边值问题（16）有解.

注1 上述F′（t）是Henstock－Kurzweil可积但不是Lebesgue可积的，因此不能应用文献［1］中定理2.3.

例3 考虑反周期边值问题：

证明：设f1（x，t）＝t2x＋φ（x，t），f2（t）＝H′，则f1关于x连续，f2在［0，1］上DHK可积.由推论2知，反周期边值问题（19）有解.

［1］WANG Kaizhi.A New Existence Result for Nonlinear First－Order Anti－periodic Boundary Problems［J］.Appl Math Lett，2008，21：1149－1154.

［2］Franco D，Nieto J，O’Regan D.Anti－periodic Boundary Value Problem for Nonlinear First Order Ordinary Differential Equations［J］.Math Inequal Appl，2003，6：477－485.

［3］Aftabizadeh A，Pavel N H，Huang Y K.Anti－periodic Oscillations of Some Second－Order Differential Equations and Optimal Control Problems［J］.J Comput Appl Math，1994，52（1／2／3）：3－21.

［4］Aftabizadeh A R，Huang Y K，Pavel N H.Nonlinear Third－Order Differential Equations with Anti－periodic Boundary Conditions and Some Optimal Control Problems［J］.J Math Anal Appl，1995，192（1）：266－293.

［5］Aizicovici S，Reich S.Anti－periodic Solutions to a Class of Non－monotone Evolution Equations ［J］.Discrete Contin Dynam Systems，1999，5（1）：35－42.

［6］Aizicovici S，Pavel N H.Anti－periodic Solutions to a Class of Nonlinear Differential Equations in Hilbert Space［J］.J Funet Anal，1991，99（2）：387－408.

［7］Lee P Y.Lanzhou Lectures on Henstock Integration［M］.Singapore：World Scientific Publishing Company，1989.

［8］ZHOU Xueyuan，YE Guoju.Second Order Periodic Boundary Value Problems Involving the Distributional Henstock－Kurzweil Integral［J］.Advances in Pure Mathematics，2012，2（5）：330－336.

［9］LU Yueping，YE Guoju，WANG Ying，et al.Existence of Solutions of the Wave Equation Involving the Distributional Henstock－Kurzweil Integral［J］.Differential and Integral Equations，2011，24（11／12）：1063－1071.

［10］XUE Xiaoping，ZHANG Bo.Properties of Set－Valued Function with Bounded Variation in Banach Space ［J］.Journal of Harbin Institute of Technology，1991（3）：102－107.

［11］Zeidler E.Applied Functinal Analysis：Applications to Mathematical Physics［M］.New York：Springer－Verlag，1995.