部分函数型线性回归模型的预平滑估计

张 雪，田 媛，王德辉

（吉林大学 数学学院，长春130012）

由于函数型数据的特殊性，将经典多元回归方法应用到函数型回归模型上通常不能得到较好的结果，因此出现了许多处理这类问题的方法.文献［1］介绍了函数型线性模型的3种类型：向量型响应变量函数型解释变量、函数型响应变量向量型解释变量及响应变量和解释变量均为函数型.文献［2］讨论了函数型线性模型.更一般地，在不满足线性假设的情况下，文献［3］介绍了非参数函数型数据，研究了对连接函数的估计问题.文献［4］用非参数方法建立了线性回归系数的估计.当变量中既有向量型又有函数型时，称其为混合数据.文献［5］介绍了针对混合数据的部分函数型线性模型，该模型结合经典的多元线性模型和函数型线性模型，具有独特的优越性.在处理函数型线性模型时，主成分分析是一种非常重要的方法，文献［6］介绍了函数主成分分析的性质.文献［7］通过把L2空间的函数型数据进行K－L展开，给出了部分函数型线性模型中系数的估计量，并讨论了估计量的渐近性质，但当函数型数据协方差算子的特征值只有少数非零时，该估计的结果与真实值相差较多.本文基于文献［8］的思想，采用预平滑方法对文献［7］中给出的估计量进行修正，得到新的相合估计量，解决了上述问题.

1 部分函数型线性模型

部分函数型线性模型［5］，即标量返回值Y与预测值（z，X）满足如下线性关系：

其中：z＝（z1，z2，…，zp）T为p维随机向量，Ez＝0，Ezz′存在且有限；｛X（t）｝∈L2［0，1］为随机过程，均值为零，

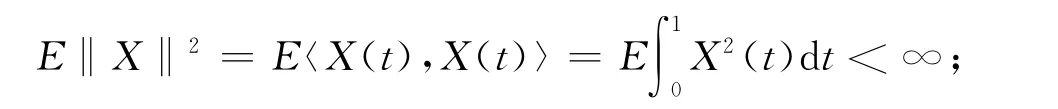
ε与z，X 相互独立，且Eε＝0，Varε＝σ2；θ（t）∈L2［0，1］且‖θ‖2＜∞；β为p 维向量.

特别地，当β＝0时，模型（1）为Y＝〈θ（t），X（t）〉＋ε，即函数型线性模型，当θ＝0时，模型（1）为Y＝βTz＋ε，即多元线性模型，故本文方法同样适用于这两种情况.

记过程X 的协方差函数KX（s，t）＝Cov（X（s），X（t）），｛（λj，φj）｝j为协方差算子 K（x）（t）＝〈x（s），KX（s，t）〉的特征值和特征函数，即满足 K（φj）＝λjφj.类似地，记 KYX（·）＝ Cov（Y，X（·）），KzX（·）＝Cov（z，X（·））＝ （Kz1X（·），…，KzpX（·））T，Kz＝ Var（z），KzY＝Cov（z，Y）.

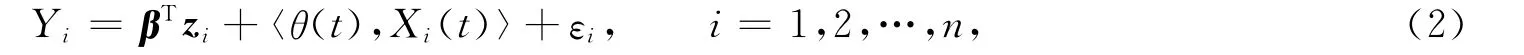
根据文献［7］采用主成分分析方法，选择前m个最大特征值对应的主成分将θ（t）和X（t）进行K－L展开，使用最小二乘方法得到估计量：

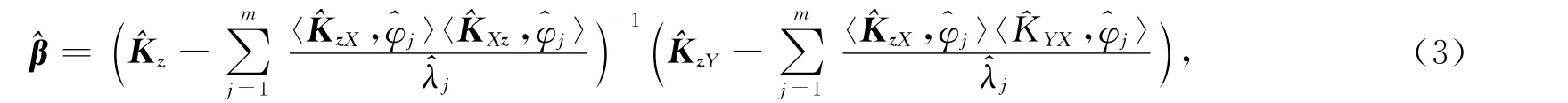
2 估计量的构造及相合性

由文献［7］可知，β和θ的估计量中都有＾λj做分母，因此对于只有少数非零特征值的函数型样本，通过模拟可知这种估计量非常不稳定，因此本文采用预平滑方法对估计量进行修正：令｛αn｝n为一列趋于0的正实数.给出新的估计量：

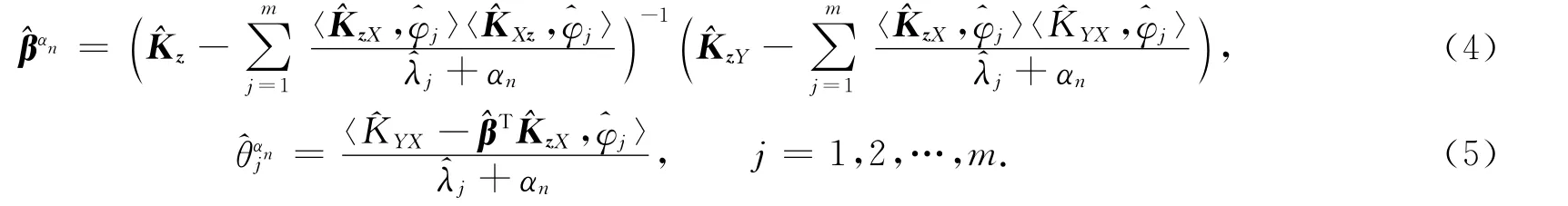
式（4）和式（5）通过对分式分母的处理解决了分母趋于零的问题，使得估计量更稳定.

估计量的相合性需要如下假设：

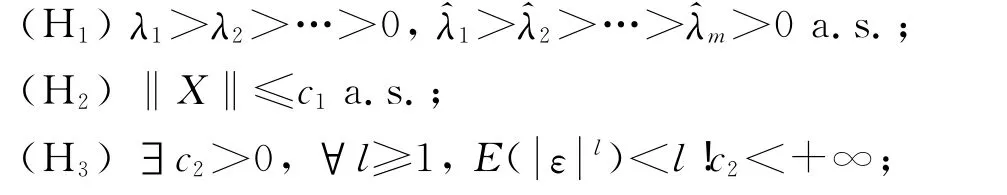
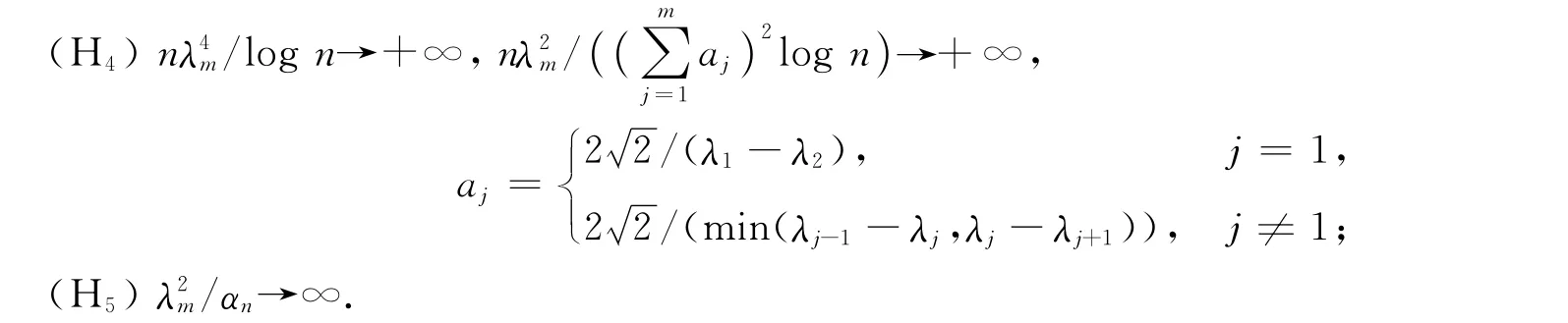
定理1 在假设（H1）～（H5）下，

定理2 在假设（H1）～（H5）下，‖＾θαn－θ‖→0a.s.

定理1和定理2表明，在一定的条件下本文给出的系数函数估计量和系数向量估计量具有相合性.

下面证明定理1和定理2.定理1的证明类似于文献［7］中定理3.1的证明，所用符号也与文献［7］相对应，不同处将用上标αn标注.

引理1 令

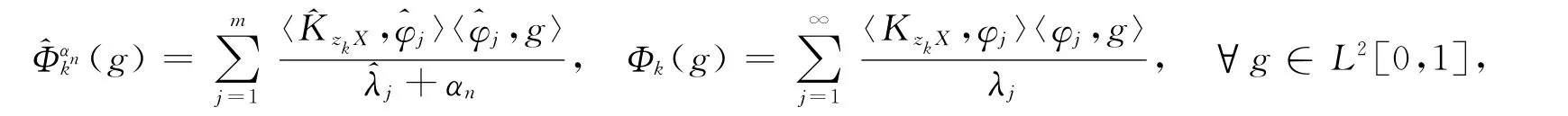
则有

证明：由于

2.1 定理1的证明

首先注意到

由于z（k）＝g（k）＋η（k），故

其中：g（k）＝（〈gk，X1〉，…，〈gk，Xn〉）T；η（k）＝（η1k，…，ηnk）T.经计算可得

因为

故

同理可得

根据文献［7］，

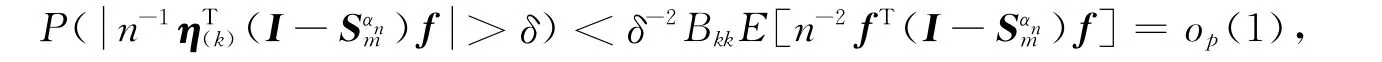
其中Bkk为B的第k个对角线元素.从而得

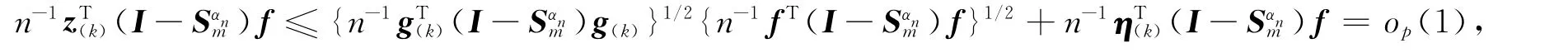
即

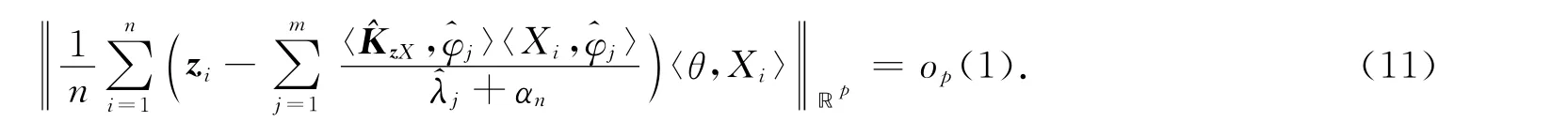
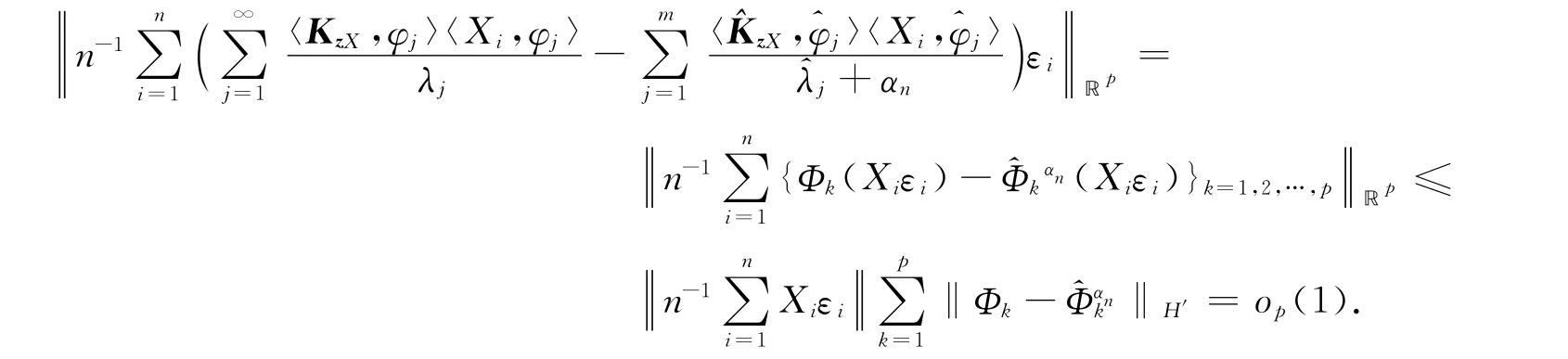
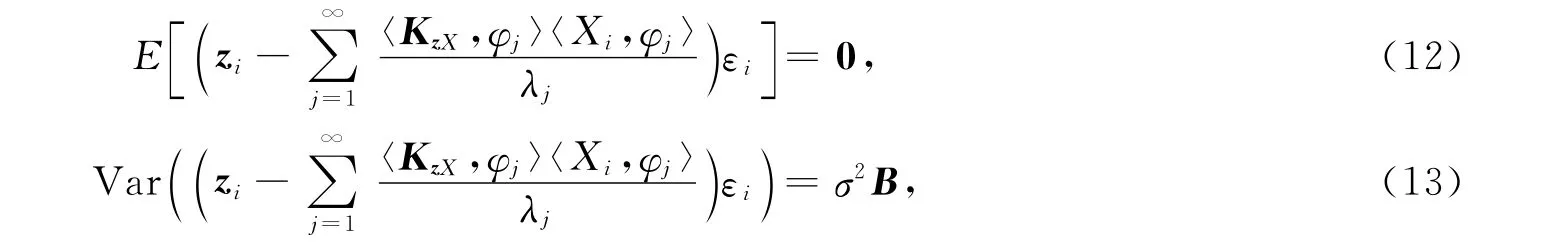
从而

2.2 定理2的证明

3 数值模拟

下面给出一个实例，比较Shin［7］给出的估计量和本文提出的估计量.在模型（1）中，令

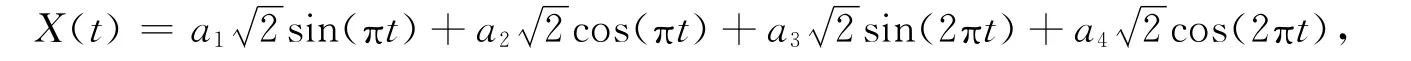
分别为预测值的均方误差、估计θ的均方误差和估计β的均方误差，其中p为维数.

表1 两种估计量的均方误差Table 1 Mean square error for two types of estimators

由表1可见，当m≤3时两种估计量的效果几乎相同，由Shin提出的估计量在m＝4时达到最优；当m＞4时，由于趋于零的特征值在分母上产生较大波动，所以不能给出准确的估计，很明显本文给出的估计量具有较好的稳定性，而且优于Shin的结果，表明在处理这类数据时使用本文的估计量可以选取适当大的m值而不必计算m的最优值.

［1］Ramsay J O，Silverman B W.Functional Data Analysis［M］.2nd ed.New York：Springer，2005：217－295.

［2］Cardot H，Ferraty F，Sarda P.Functional Linear Model ［J］.Statistics ＆ Probability Letters，1999，45（1）：11－22.

［3］Ferraty F，Vieu P.Nonparametric Functional Data Analysis［M］.New York：Springer，2006.

［4］Cristobal J A C，Roca F P，Manteiga W G.A Class of Linear Regression Parameter Estimators Constructed by Nonparametric Estimation［J］.The Annals of Statistics，1987，15（2）：603－609.

［5］Zhang D，Lin X，Sowers M F.Two－Stage Functional Mixed Models for Evaluating the Effect of Longitudinal Covariate Profiles on a Scalar Outcome［J］.Biometrics，2007，63：351－362.

［6］Hall P，Hosseini－Nasab M.On Properties of Functional Principal Components Analysis［J］.Journal of the Royal Statistical Society：Ser B，2006，68（1）：109－126.

［7］Shin H.Partial Functional Linear Regression［J］.Journal of Statistical Planning and Inference，2009，139（10）：3405－3418.

［8］Ferraty F，González－Manteiga W，Martínez－Calvo A，et al.Presmoothing in Functional Linear Regression ［J］.Statistica Sinica，2012，22：69－94.