一类分数阶椭圆型方程解的存在性

关丽红，常 晶，赵 昕

（1.长春大学 理学院，长春130022；2.空军航空大学 基础部，长春130022；3.吉林农业大学 信息技术学院，长春130118）

考虑如下分数阶椭圆型方程Dirichlet边值问题：

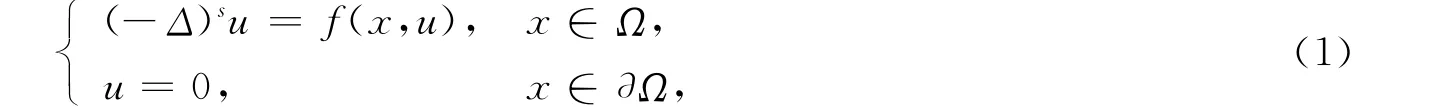
其中：Ω⊂ℝN（N≥2）是带有光滑边界∂Ω的有界区域；（－Δ）s表示分数阶Laplace算子，s∈（0，1）；f∈C（¯Ω×ℝ，ℝ）.目前，关于分数阶椭圆型方程解的存在性与多重性研究已有许多结果［1－6］.分数阶Laplace算子（－Δ）s是Lévy稳态扩散过程的无穷小生成元［7］，在美式期权、人口动力学和黏弹性力学等领域应用广泛［8－10］.本文研究分数阶椭圆型方程Dirichlet边值问题（1）非平凡解的存在性，应用推广形式的山路定理，在非线性项满足渐近线性增长的情形下得到了问题（1）非平凡解的存在性.

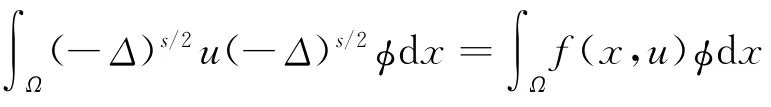
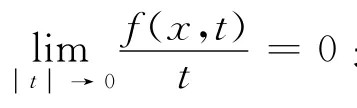
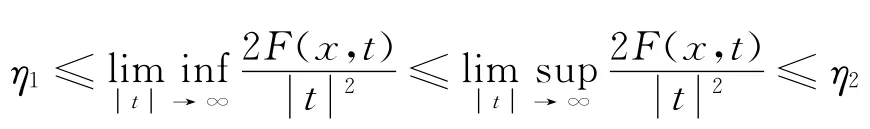
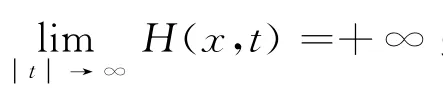
本文主要结果如下：

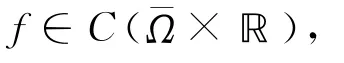
注1 文献［3，5］分别研究了分数阶Schrödinger方程（－Δ）su＋V（x）u＝f（x，u）在非线性项满足渐近线性增长和超线性增长时解的存在性；文献［6］在非线性项满足超线性增长时得到了分数阶Laplace方程（－Δ）su＝f（x，u）解的多重性；文献［1］在非线性项满足临界增长时，得到了问题（1）解的多重性；文献［2］在非线性项满足超线性增长时，得到了问题（1）解的多重性.本文在非线性项满足渐近线性增长时，研究问题（1）非平凡解的存在性.

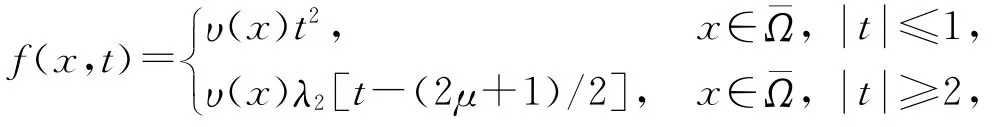
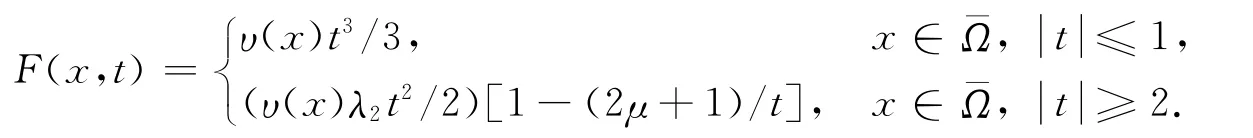
通常如果I∈C1（E，ℝ），并且序列｛un｝⊂E 满足I（un）→c，（1＋‖un‖）‖I′（un）‖→0当n→＋∞，则称｛un｝为泛函I的一个Cerami序列，简记为（C）c序列.如果I的每个Cerami序列都有强收敛子列，则称I满足（C）c条件.

下面证明定理1.由假设（H1）～（H3）易知泛函J具有山路几何，即：

1）存在r，δ＞0，使得对所有满足‖u‖＝r的u∈Hs0（Ω），都有J（u）≥δ；

2）J（tφ1）→－∞，t→＋∞.

为了应用定理2，只需证明泛函J满足（C）c条件.取｛un｝n∈ℕ⊂Hs0（Ω）为（C）c序列，即

往证序列｛un｝在Hs0（Ω）中一致有界.事实上，若不然，不妨设‖un‖→＋∞（n→＋∞）.由式（2）可得

由假设（H4），对任意的ε＞0，存在M＞0，使得

令zn＝un／‖un‖2.则存在｛zn｝的子列（不妨仍记为｛zn｝）及z0∈（Ω），使得zn⇀z0，且zn（x）→z0（x），a.e.x∈Ω.由式（4）可得因此，存在Ω1⊂Ω，使得且z0（x）≠0，a.e.x∈Ω1.因此，对a.e.x∈Ω1，有

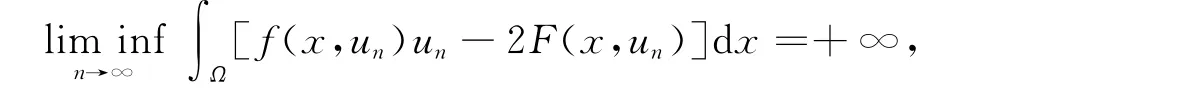
这与式（3）矛盾.因此｛un｝在（Ω）中有界，从而利用标准的讨论可知，存在u0∈（Ω），使得又由假设（H3）和Fatou引理可得应用定理2，显然u0即是问题（1）的非平凡弱解.证毕.

衷心感谢吉林大学数学学院李勇教授的鼓励和悉心指导.

［1］Barrios B，Colorado E，Pablo A，de，et al.On Some Critical Problems for the Fractional Laplacian Operator［J］.J Differential Equations，2012，252（11）：6133－6162.

［2］Brändle C，Colorado E，Pablo A，de.A Concave－Convex Elliptic Problem Involving the Fractional Laplacian［J］.Proc Roy Soc Edinburgh Sect A，2013，143（1）：39－71.

［3］CHANG Xiaojun.Ground State Solutions of Asymptotically Linear Fractional Schrödinger Equations［J］.J Math Phys，2013，54（6）：061504.

［4］CHANG Xiaojun，WANG Zhiqiang.Ground State of Scalar Field Equations Involving a Fractional Laplacian with General Nonlinearity［J］.Nonlinearity，2013，26（2）：479－494.

［5］Felmer P，Quaas A，TAN Jinggang.Positive Solutions of Nonlinear Schrödinger Equation with the Fractional Laplacian［J］.Proc Roy Soc Edinburgh Sect A，2012，142（6）：1237－1262.

［6］Servadei R，Valdinoci E.Mountain Pass Solutions for Non－local Elliptic Operators［J］.J Math Anal Appl，2012，389（2）：887－898.

［7］Bertoin J.Lévy Processes［M］.Cambridge：Cambridge University Press，1996.

［8］Applebaum D.Lévy Processes－From Probability to Finance and Quantum Groups［J］.Notices Amer Math Soc，2004，51（11）：1336－1347.

［9］Garroni A，Müller S.Γ－Limit of a Phase－Field Model of Dislocations［J］.SIAM J Math Anal，2005，36（6）：1943－1964.

［10］Valdinoci E.From the Long Jump Random Walk to the Fractional Laplacian［J］.Bol Soc Esp Mat Apl SMA，2009，49：33－44.

［11］Rabinowitz P H.Minimax Methods in Critical Point Theory with Applications to Differential Equations［M］.Vol.65.Providence，RI：American Mathematical Society，1986.

［12］Schechter M.A Variation of the Mountain Pass Lemma and Applications［J］.J London Math Soc，1991，44（3）：491－502.