(2+1)维Kadomtsov-Petviashvili-Joseph- Egri方程的李对称分析和精确解

李 宁，刘希强

(2+1)维Kadomtsov-Petviashvili-Joseph- Egri方程的李对称分析和精确解

*李 宁，刘希强

(聊城大学数学科学学院，山东，聊城 252059)

利用经典李群方法，得到 (2+1)维Kadomtsov-Petviashvili-Joseph-Egri方程的经典李点对称，并利用对称得到该方程的一些相似约化，通过求解约化方程，得到了该方程的很多精确解，包括双曲函数解，雅可比椭圆函数解，三角函数解，有理函数解，幂级数解等。

经典李群方法；(2+1)维Kadomtsov-Petviashvili-Joseph-Egri方程；精确解；对称；约化

随着科技的发展，人们对非线性发展方程越来越关注，寻找非线性发展方程的精确解就变得更为重要。为了求解非线性发展方程的精确解，国内外学者提出很多行之有效的方法如雅克比椭圆函数展开法[1]，tanh展开法[2]，经典和非经典李群方法[3-6]，指数函数展开法[7-8]，贝克隆变换法[9]，广义代数法[10]等。其中，经典李群方法是最有效的方法之一。本文将利用经典李群方法考虑以下(2+1)维Kadomtsov-Petviashvili-Joseph-Egri ( KP-JE )方程

本文组成如下：第一部分，给出经典对称的定义和相关结论，并利用其得到了方程(1)的经典对称；第二部分，利用得到的对称对方程(1)进行约化求解，并得到了一些新精确解；第三部分给出简单的结论。

1 KP-JE的经典对称

以下考虑N阶非线性发展方程

首先给出经典对称[12]的定义和一个相关定理[13]

定义 1 经典李点对称

如果方程(2)是在以下变换下的一个不变量

称为一个经典李点对称，简称对称。

定理 1 如果向量场 (4) 是方程(2)的一个李点对称当且仅当

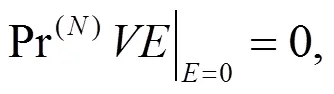
其中

是向量场的阶延拓。

以下利用定理1求解方程(1)李点对称。方程(1)的向量场可以表示为

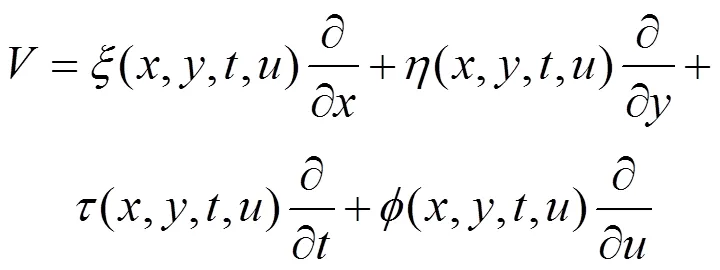
由定理1可以得到(5)四阶延拓

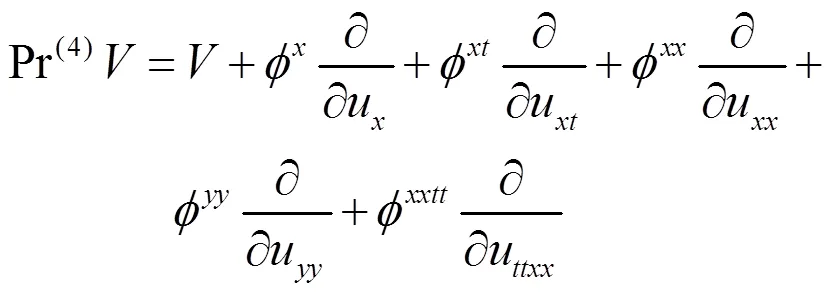
利用李群方法，解超定方程组可得方程(1)李点对称为

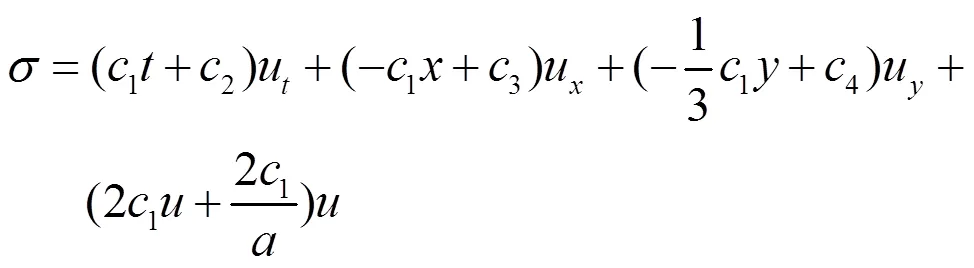
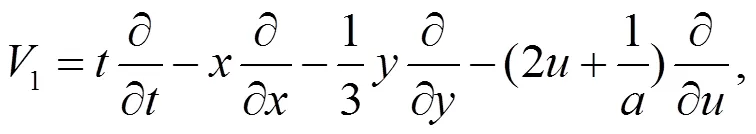
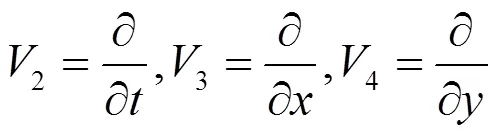
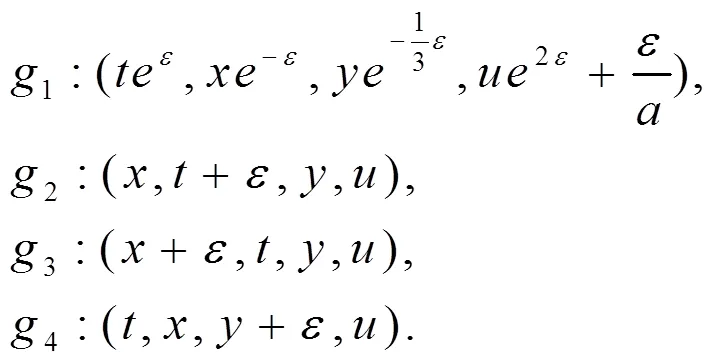
对称群2，3和4表示方程(1)解的时空不变性，1表示方程(1)解伽利略伸缩不变性。由以上对称群1，2，3和4，可以得到方程(1)的不变解为

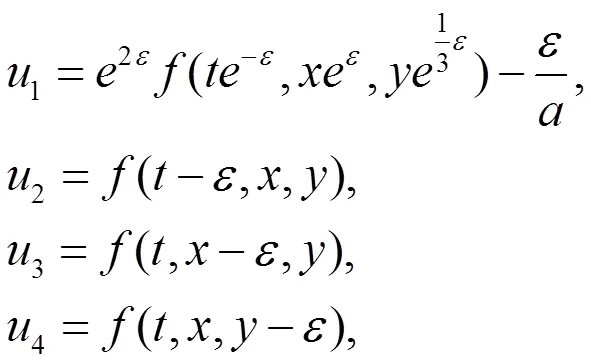
如果选取文献[11]中方程(1)的一个三角周期解

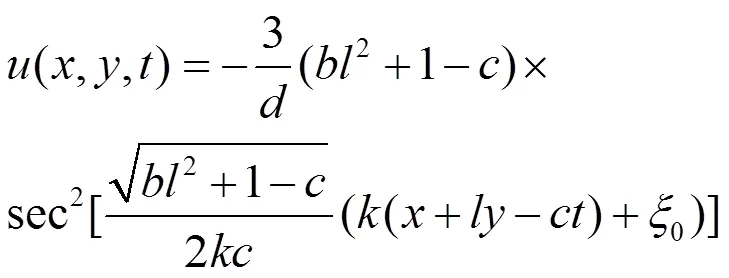
注1利用以上不变解(9)与文献[11]中的解，可以得到方程(1)更多的新精确解，由此文献[11]中的解得到了推广。

2 KP-JE方程的相似约化和精确解

为了得到方程(1)的精确解，须先求解以下特征方程组

解方程组(10)，得到以下三组约化方程 (参见表1)。

表1 方程(1)的相似约化方程

以下考虑情况1和情况2。

情况 1

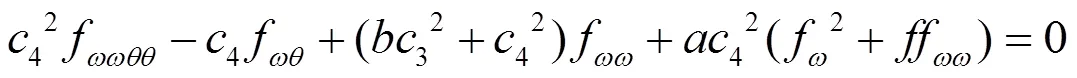
为了求解方程(11)，以下再次利用李群方法约化方程(11)。

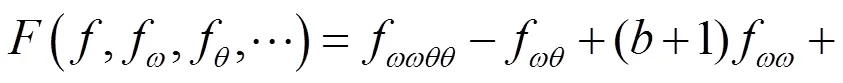
方程(12)相应的向量场可设为

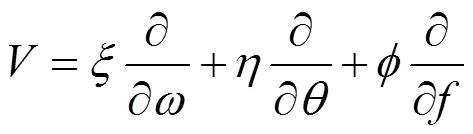
重复以上过程，可得方程(12)李点对称为

从而得到相应的特征方程组为

类似地，解方程组(15) ，得到以下两组相似约化方程(参见表2)。

表2 方程(11)的相似约化方程

情况1.1

(17)

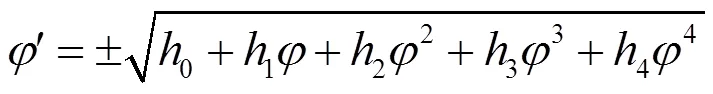
将(18) 和(17) 带入 (16) ，可得以下两组解

情况1.1.1

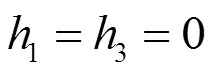
情况1.1.2

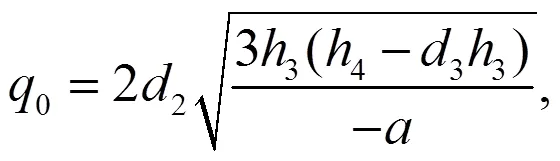
其中是非零常数。

情况1.1.1 (a) 雅克比椭圆函数解

情况1.1.1 (b) 钟状解 (见图1)

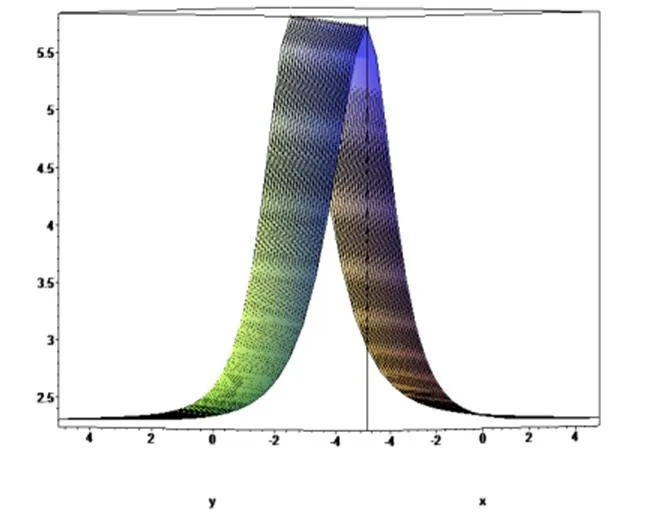
图1 解ub.1 (钟状解) 参数为

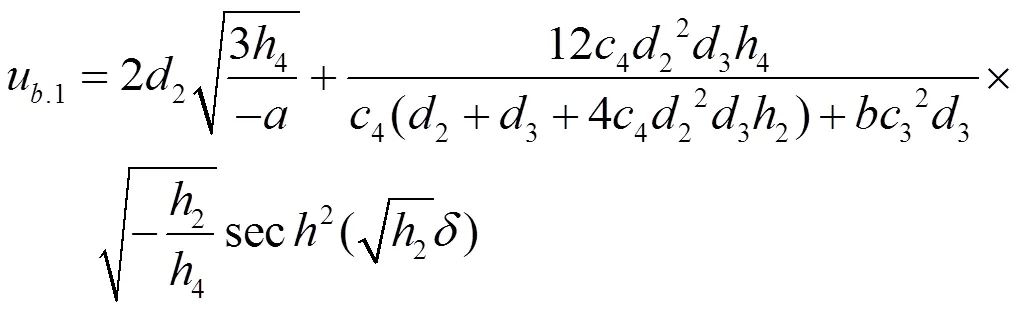
情况1.1.1 (c) 扭结状解(见图2)

情况1.1.1(d) 奇异解

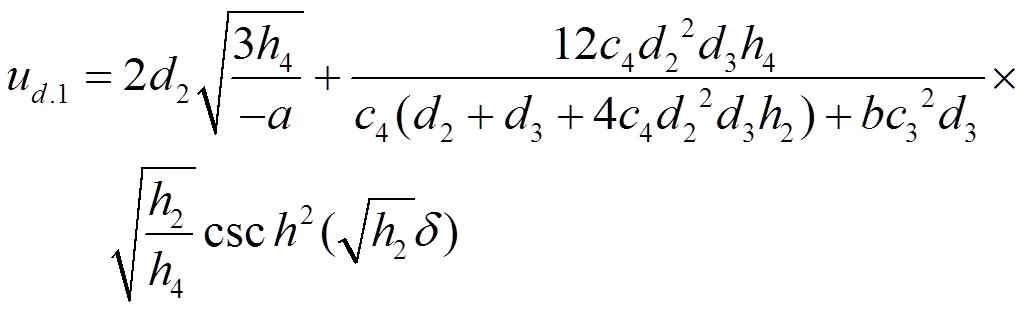
情况1.1.1 (e) 三角周期解 (见图3)

情况 1.1.2 (a) 有理函数解

情况1.1.2 (b) 三角周期解(见图4)

图4 解ug.1 (三角周期解)参数为

Fig. 4 Solution ug.1 is shown at (triangular profile solution)

情况 1.2

以下利用幂级数法求解方程(19)的解，设方程(19)有以下形式的解

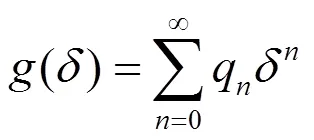
由方程(19)，得到

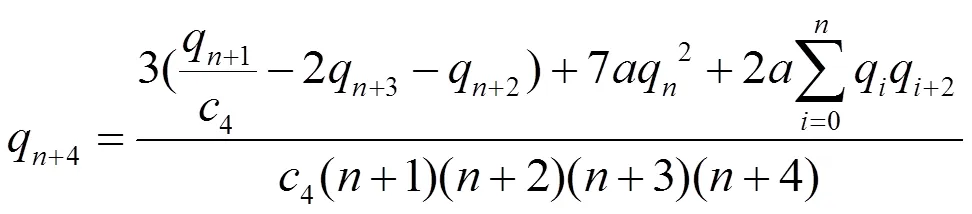
由以上过程，可得方程(1) 的幂级数解为

情况2

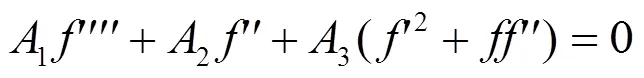
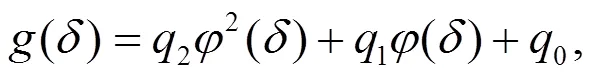
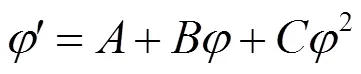
将(26) 和(27)代入(25)，得到

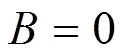
由此可以得到以下解：

情况2.1 (a) 双曲函数解

情况 2.1 (b) 三角周期解

假设方程(25) 有以下形式的解

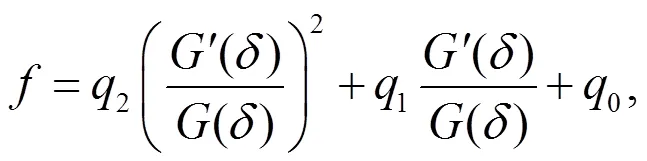
将(29)和(30)代入(25)，可得

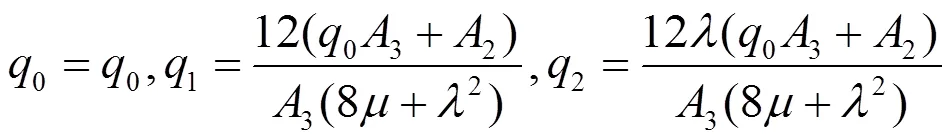
得到以下三种形式的解：

情况 3与情况 1.2类似，此处省略。

注 2 本文得到的方程(1)的精确解均已经Maple软件检验。

3 结论

本文利用经典李群方法研究了KP-JE方程，得到该方程的李点对称，李代数和相似约化。通过使用再次李群方法，把KP-JE方程约化为常微分方程，得到了该方程多种精确解，这些解在解释复杂物理现象有很重要的作用。

[1] Fan Engui, Zhang Jian. Applications of the Jacobi elliptic function method to special-type nonlinear equations [J]. Phys. Lett. A, 2002, 305: 383-392.

[2] Wazwaz A M. The extended tanh method for new compact and noncompact solutions for the KP-BBM and the ZK-BBM equations [J]. Chaos, Solitons and Fractals , 2008,38: 1505-1516.

[3] Zhang Yingyuan, Wang Gangwei, Liu Xiqiang. Symmetry reductions and explicit solutions of the (2+1)-dimensional nonlinear evolution equation [J]. Chinese Journal of Quantum Electromics, 2012, 29: 411-416(in Chinese).

[4] Chen Yong,Yan Zhenya, Zhang Hongqing. New explicit solitary wave solutions for (2+1)-dimensional Boussinesq equation and(3+1)-dimensional KP equation [J]. Phys. Lett. A, 2003, 307: 107-13.

[5] Liu Na, Liu Xi-qiang. Similarity reductions and similarity solutions of the (3+1)-dimensional Kadomtsev -Petviashvili equation [J]. Chin. Phys. Lett.,2008,25: 3527-3530.

[6] Chen Mei, Liu Xiqiang.Symmetries and Exact Solutions of the Breaking Soliton Equation [J].Commun. Theor. Phys., 2011, 56 : 851-855.

[7] He Jihuan. Exp-function method for nonlinear wave equation [J]. Chaos, Solitions and Fractals, 2006, 30: 700-708.

[8] He Jihuan, Abdou M A. New periodic solutions for nonlinear evolution equations using exp-function method [J].Chaos,Soliton and Fractals,2007,34: 1421-1429.

[9] Zait R A. Bäcklund transformations, cnoidal wave and traveling wave solutions of the SK and KK equations [J]. Chaos, Solitons and Fractals, 2003, 15: 673-678.

[10] Bai Chenglin, Bai Chengjie, Zhao Hong. A new generalized algebraic method and its application in nonlinear evolution equations with variable coefficients [J]. Z. Naturforsch, 2005, 60a: 211-220.

[11] Taghizadeh N, Mirzazadeh M. Analytic investigation of the KP-Joseph-Egri equation for traveling wave solutions [J]. Appl. Math, 2011, 6: 292-303.

[12] Olver P J. Applications of Lie group to differential equations [M]. New York: Springer, 1993.

[13] Tang Xiaoyang, Qian Xianmin, Ji Lin, et al. Conditional similarity reductions of the (2+1)- dimensional KdV equation via the extended Lie group approach [J]. J. Phys. Soc. Japan, 2004, 6: 1464-1475.

[14] Zhao Xue-qin, Zhi Hong-yan, Zhang Hong-qing. Improved Jacobi-function method with symbolic computation to construct new double-periodic solutions for the Generalized Ito system [J]. Chaos, solitons and Fractals, 2006, 28: 112-116.

[15] Wang Dengshan, Li Hongbo. Elliptic equation’s new solutions and their applications to two nonlinear partial differential equations [J]. Appl. Math.Comput, 2007, 188: 762-771.

[16] Yomba E. On exact solutions of the coupled Klein–Gordon–Schrödinger and the complex coupled KdV equations using mapping method [J].Chaos, solitons and Fractals, 2004, 2: 209-229.

[17] Lu Dianchen, Hong Baojian. New exact solutions for the (2+1)-dimensional Generalized Broer-Kaup system[J]. Appl. Math. Comput, 2008, 199: 572-580.

LIE SYMMETRY ANALYSIS AND EXACT SOLUTION OF (2+1)-DIMENSIONAL KADOMTSOV-PETVIASHVILI-JOSEPH- EGRI EQUATION

*LI Ning，LIU Xi-qiang

(School of Mathematical Sciences, Liaocheng University, Liaocheng, Shandong 252059, China)

Based onthe classical Lie group method, we obtain the classical Lie point symmetry of the (2+1)-dimensional Kadomtsov-Petviashvili-Joseph-Egri (KP-JE for short) equation. Using the symmetries, we find some classical similarity reductions of KP-JE equation. Many kinds of exact solutions of the KP-JE equation are derived by solving the reduced equations, including the elliptic functions , the rational functions，the hyperbolic functions, the trigonometric functions, the power series solution.

classical Lie group method; (2+1)-dimensional KP-JE equation; exact solutions; symmetry; reduction

O175.29

A

10.3969/j.issn.1674-8085.2014.02.002

1674-8085(2014)02-0007-07

2013-05-23；

2013-07-16

国家自然科学基金和中国工程物理研究院联合基金项目(11076015)

*李 宁(1981-)，男，山东枣庄人，硕士生，主要从事非线性偏微分方程解的研究(E-mail:ln1011@163.com);

刘希强(1957-)，男，山东菏泽人，教授，博士，主要从事非线性微分方程系统研究(E-mail: liuxiq@sina.com).