Flow choking characteristics of slit-type energy dissipaters*

WU Jian-hua （吴建华）, WAN Bin （万彬）, MA Fei （马飞）, LI Tong-chun （李同春）

National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China, E-mail: jhwu@hhu.edu.cn

Flow choking characteristics of slit-type energy dissipaters*

WU Jian-hua （吴建华）, WAN Bin （万彬）, MA Fei （马飞）, LI Tong-chun （李同春）

National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China, E-mail: jhwu@hhu.edu.cn

(Received November 25, 2014, Revised December 14, 2014)

In this paper, the behavior of the flow choking, including the critical and developing states, was experimentally investigated by means of five slit-type outlets, characterized by the outlet width, the contraction angle and the opening of the working gate. The results showed that the approach flow Froude number of the critical choking decreases if the outlet width increases, or the contraction angle decreases, or the opening increases. There is the hysteresis when the flow choking develops, i.e., the Froude numbers of the appearance and disappearance of the flow choking at the increasing discharge regime are all larger than those at the decreasing discharge regime. For various widths of the outlets, the differences between the critical Froude numbers at small opening are much larger than thoset at large opening. The change range from appearance to disappearance of the flow choking at small opening is smaller than that at large opening.

flow choking, slit-type energy dissipater, partial opening, Froude number

Contraction type energy dissipaters, like flaring pier, slit-type and deflector, are widely used in hydropower projects, thanks to the simple structure and high energy dissipation[1,2]. The flow choking, a kind of special hydraulic phenomena that may occur when the supercritical flow passes through any obstruction[3], will bring about the effects on the operation of release works[4]. The behavior of the flow choking, characterized by the approach flow Froude number, is related to the geometric parameters for the various structural forms of the outlet.

Juon and Hager[5]observed the flow regimes through the flip buckets without and with deflectors and presented the choking criterion. They deemed that the Froude number of the flow choking was related to the relative bucket height and deflector angle. With regard to the flip buckets, Stenier et al.[6], and Heller et al.[7]gave the flow choking conditions for the increasing and decreasing discharge regimes, which are also the relationships between the Froude number and relative bucket height. Lucas et al.[8]proposed that the Froude number of the flow choking for the tetrahedron outlets was the function of their geometric parameters, like the length and width of the tetrahedron, and relative width of the channel. For the multiple slit-type energy dissipaters, Wu et al.[9]presented that the Froude number of the flow choking decreased with the increasing numbers of the outlet slits, and the Froude number greatly fell comparing the conventional slit-type outlets.

The objectives of this paper are to experimentally investigate the behavior of the flow choking for the slit-type energy dissipaters, including the critical and developing states from the increasing and decreasing discharge regimes on the basis of the outlet width, the contraction angle and the opening of the working gate.

The experiments were conducted in High-speed Flow Laboratory, Hohai University (Nanjing, China). The experimental setup consisted of a pump, an approach conduit, a large feeding basin, a test model, and a flow return system (Fig.1(a)). The feeding basin issued an approach (subscript o) flow of depthoh and average velocityov, resulting in the approach flow Froude number Fr=v/(gh)1/2. The discharges oo Q were measured with discharge measurement weir instruments. The maximum pump capacity was 400 Ls–1, and the working head was 1.50 m.

Fig.1 Defnition sketch for experimental setup

The test model, made of perspex, included two parts with pressure and free-surface flow sections, which was separated through a working gate with the height of HG=0.18 m . The part with pressure flow was 0.65 m long, 0.15 m wide and 0.19 m high, and its height was reduced to 0.18 m in the location of the gate by means of the top slope of 1:8. In the part of free-surface flow, it was 0.55 m long, 0.15 m wide and 0.30 m high with the slit-type energy dissipater in the outlet. The geometry of the outlet was showed in Fig.1(b). The channel width of B=0.15 m was reduced to b in the edge of the outlet in the length of L, and the contraction angle was given by =θ arctan[(B-b)/2].

Table1 Cases and geometric parameters of models

Table 1 lists the cases and geometric parameters of the models, and those cases were divided into two sets. Cases M1-M3 serve as the effects of b, while Cases M3-M5 are for the effects of θ. In addition, the behavior was investigated at the partial opening of the working gate by Cases M1 and M2, and the opening was given by e=hp/HG, where hpis the opening height of the gate.

For a slit-type energy dissipater, the flow choking will occur due to the contraction effect in the outlet. Figure 2 shows the developing process of the flow choking (Case M2) under the conditions of the entirely opening of the gate. The appearance, formation, development and disappearance of the choking grow successively with the increasing discharge Q or the approach flow Froude number Fr (Fig.2 (a)-2(d)).

Fig.2 Process of flow choking (M2)

At the phase of the appearance of the flow choking, the roller appears just on some flow surface inthe contraction section, and in this state, the flow depth in the location of the gate is larger than the outlet height of the pressure flow (Fig.2(a)). Subsequently, this roller is formed on the whole surface of the free flow. Here, it may be act as a fixed state to conveniently repeat this phenomenon and is defined as the critical flow choking[8], expressed by the critical (subscript C) Froude numberCFr (Fig.2(b)). Furthermore, the flow choking will develop (Fig.2(c)) and then disappear (Fig.2(d)) when the approach flow Froude number Fr increases.

On the other hand, there was the developing range from appearance to disappearance of the flow choking, and the change of the choking behavior should be paid good attention to for various hydraulic or geometric parameters.

Fig.3 Variations of Fr with /b B at same θ (Cases M1-M3)

Figure 3 shows the variations of Fr with /b B at the same contraction angle θ (Cases M1-M3). In this figures,andare the Froude numbers at the appearance and disappearance of the flow choking, respectively, as the increasing (sign +) discharge regime, whileandare those as the decreasing (sign –) discharge regime.

Fig.4 Variation ofCFr with /b B at same θ (Cases M1-M3)

Similar to the upper and lower critical Reynolds numbers, there are differences between bothand, or bothand. Clearly, it is due to the hysteresis of the developing process of the flow choking that eitheris larger thanoris larger than. Besides, it could be seen that, Fr will decreases if /b B increases (Fig.3). It should be directly related to the resistance effect resulted from the geometry of the contraction outlet.

Figure 4 demonstrates the variation ofCFr with b/ B at same θ (Cases M1-M3). FrC( b/ B) presents the linear relationships, and large /b B supports to avoid the occurrence of the flow choking.

Figure 5 is the variations of Fr with θ at the same outlet width /b B (M3 – M5). Like the changes of b/ B (Fig.3), also, eitheris larger thanoris larger than. In addition, the Froude numbers increase with the increasing contraction angle, which means that, under the condition of the same width of the outlet, small contraction angle produces small resistance of the flow, thus low approach flow Froude number.

Fig.5 Variations of Fr with θ at same /b B (Cases M3-M5)

Fig.6 Variation ofCFr with θ at same /b B (Cases M3-M5)

Figure 6 shows the variations ofCFr with θ at the same /b B (M3-M5). CFr increases linearly when θ increases in the range of the contraction angle from 8oto 13o.

On the basis of the observations of flow regimes, the characteristics of the flow choking at the partialopening of the working gate were experimentally investigated, including the opening e=hp/HG=0.25, 0.50, 0.75 and 1.00. Figure 7 presents the variations of FrCwith e (Cases M1and M2). FrC( e) decreases monotonously for both case M1 and M2. Meanwhile, the outlet width /b B has the effect on the critical Froude numberCFr in the various opening e of the gate. The differences between cases M1 and M2 are 0.51 and 0.16 at =e0.25 and 1.00, respectively.

Fig.7 Variations ofCFr with e at same θ (cases M1and M2)

Fig.8 Variations of Fr with e for case M1

Fig.9 Variations of Fr with e for case M2

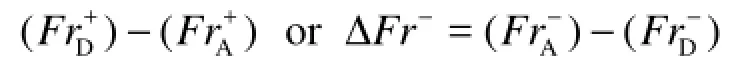
In summary, where the outlet work with a slittype energy dissipater was concerned, it is significant to understand the behavior of the flow choking under the conditions of various hydraulic and geometric parameters.

Both large width /b B and small contraction angle θ support to decrease the Froude numberCFr of the critical flow choking.

Like the upper and lower critical Reynolds numbers, the Froude numbers of the appearance (and disappearance (in the increasing discharge regime are all larger than those (and) in the decreasing discharge regime, respectively, due to the hysteresis of the choking development.

When the working gates are partially opened, the Froude numberCFr of the critical flow choking decreases with the increasing opening, but the outlet width /b B at small opening has larger effect onCFr than that at large opening. Meanwhile, the range producing the flow choking at small opening is smaller than that at large opening for a same geometric outlet.

[1] LI Nai-wen, XU Wei-lin and ZHOU Mao-lin et al. Experimental study on energy dissipation of flood discharge in high arch dams without impact of jets in air[J]. Journal of Hydraulic Engineering, 2008, 39(8): 927-933(in Chinese).

[2] HUANG Qiu-jun, WU Jian-hua. Research on contraction energy dissipators[J]. Journal of Hohai University: Natural Sciences, 2008, 36(2): 219-223(in Chinese).

[3] VISCHER D. L., HAGER W. H. Energy dissipators[M]. Rotterdam, The Netherlands: A. A. Balkema, 1995.

[4] WANG Cai-huan, HOU Dong-mei and WANG Si-ying et al. Research and practice on narrow-slot energy dissipators of high-head andl arge-flood bank spillway[J]. Journal of Hydroelectric Engineering, 2012, 31(1): 123-128, 139(in Chinese).

[5] JUON R., HAGER W. H. Flip bucket without and with deflectors[J]. Journal of Hydraulic Engineering, ASCE, 2000, 126(11): 837-845.

[6] STEINER R., HELLER V. and HAGER W. H. et al. Deflector ski jump hydraulics[J]. Journal of Hydraulic Engineering, ASCE, 2008, 134(5): 562-571.

[7] HELLER V., HAGER W. H. and MINOR H. E. Ski jump hydraulics[J]. Journal of Hydraulic Engineering, ASCE, 2005, 131(5): 347-355.

[8] LUCAS J., HAGER W. H. and BOES R. M. Deflector effect on chute flow[J]. Journal of Hydraulic Engineering, ASCE, 2013, 139(4): 444-449.

[9] WU Jian-hua, YAO Li and MA Fei. Hydraulics of a multiple slit-type energy dissipater[J]. Journal of Hydrodynamics, 2014, 26(1): 86-93.

10.1016/S1001-6058(15)60468-1

* Project supported by the National Natural Science Foundation of China (Grant No. 51179056, 51279013).

Biography: WU Jian-hua (1958-), Male, Ph. D., Professor