基于极端值存在时的随机抽样改进方法

艾小青

（北京工业大学 经济与管理学院，北京 100124）

0 引言

严格意义上的随机抽样，要求总体每个单元都有一定的概率被抽中，被抽中的概率称作入样概率，其值要大于0小于1。对于简单随机抽样而言，在抽样阶段不借助任何辅助信息，总体单元平等对待，每个单元的入样概率都相等。总体单元中存在极端值（包括极小值和极大值两种情况）时，由于极端值的影响，总体自身的差异性较大，若直接采用随机抽样，估计量的抽样方差将较大，使得估计精度较差。

本文将对有极端值存在时的随机抽样进行处理，主要理念是对极小值单元可以从抽样框中剔除，对极大值单元可以确定为必抽单元，再进行随机抽样，使得随机抽样的抽样框不包含极端值，从而减小估计量的抽样方差。这种处理方法虽然不可避免的带来了一定的偏差或损失，但在一定条件下能有效地减小抽样方差，所以能减小总的均方误差，从而提高了估计精度。同时从定性判断的角度来说，极小值单元的影响可以小到忽略不计的程度，极大值单元的影响可以大到必然入样的程度，这也是符合逻辑的。

本文中随机抽样以简单随机抽样为例，估计量以总量估计为例，因为有极端值存在时，此时均值并没有很好的代表性，不宜估计均值，但估计总量仍然是成立的。本文将针对极小值和极大值两种情况分别讨论，从论证和例证两个角度揭示方法的应用条件和改进效果。

1 方法基础

1.1 简单随机抽样下的总量估计

1.2 删除极端值后方差的变化

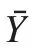
下面我们通过一个具体例子来说明。

例1：总体单元的27个值（按从小到大排列）：

以上论证是以删除一个特定值为例，删除多个特定值下也有类似的性质。该结论的意义在于：若删除极端值的干扰，使得总体自身的差异程度减小，应用于随机抽样中，将有可能使得抽样方差相应减小。

1.3 极端值的判断

在实际应用中，无法在调查之前知道哪些单元为极端值，需要借助相关辅助变量进行判断。判断要包含两个方面：一是哪些单元的取值很小（或大），二是取值是否小（或大）到可以理解为极小值（或极大值）的程度。

一般情况下，如果能找到一个与目标变量存在正向相关关系的辅助变量时，辅助变量极小，目标变量也可能极小，辅助变量极大，目标变量也可能极大。当取值与均值的偏差在正负3σ以外时，一般可理解为是极端值。

还可以参考历史数据或相关资料，或者通过定性分析来进行极端值的判断。

1.4 抽样方法优劣性的评价

一般说来，人们都是把均方误差作为评价抽样方法优劣的标准。即使有时估计量是有偏的，然后由于偏差小，估计量方差也比较小，从而使得均方误差也比较小，这时选择有偏的估计量也是更优的[1]。

本文中我们将针对极小值和极大值两种情况，分别计算新方法下估计量的均方误差，并与传统简单随机抽样下估计量的均方误差做比较，如果基于相同的总样本量，新方法下的均方误差较小，说明新方法相对更优，具有对传统抽样方法的改进效果[2]。

2 极小值存在时的情况

把极小值单元从抽样框中剔除，再进行随机抽样，虽然这不可避免的带来了系统性的偏差，但只要能更大程度的减小方差，也能使得总的均方误差减小。并且极小值单元的影响如果很小便可以忽略不计，这也是符合逻辑的。

假设确定了k个极小值单元不予调查。在总体余下的N-k个单元中，随机抽取n个单元进行调查。

总体总量的估计为：

以例1中的数据为例，若剔除k个最小单元，总量估计均方误差的结果见表1：

表1 剔除极小值后总量估计的均方误差

可见：

1、当剔除最小单元的数量不超过5个时，均方误差都会相比99203有所减小。

2、当剔除3个最小单元时，均方误差减小的幅度最大，减小为86256。

所以，当总体单元中存在极小值，并且能判断出哪些单元是极小值时，该方法将有较好的应用效果。

特别说明的是，若事先无法判断极小值的情况，便不能轻易的剔除单元，以例1中的数据为例，若随机剔除k个单元，总量估计均方误差的结果见表2：

表2 随机剔除单元后总量估计的均方误差（一次模拟结果）

可见，在剔除单元的时候一定要慎重，否则将会有适得其反的结果。因为某些单元的取值可能并不是极小，却被剔除了，这样将使得估计的误差增加。剔除单元数量越多，误差就越大。

3 极大值存在时的情况

把极大值单元确定为必抽单元，再进行一定数量的随机抽样，在总样本量一定的限制下，随机抽样的样本量有一定程度的减小，只要能使得总的均方误差减小，该方法也是更优的。并且极大值单元的影响如果大到必抽的程度，这也是符合逻辑的。

假设确定了k个极大值单元作为必抽单元。在总体余下的N-k个单元中，再随机抽取n-k个单元进行调查。

总体总量的估计为：

仍以例1中的数据为例，若把k个最大单元确定为必抽单元，总量估计均方误差的结果见表3：

表3 确定必抽单元后总量估计的均方误差

可见：

（1）因为总的样本量是10，所以必抽单元的确定个数最大为9。所有这9种情况下，均方误差都会相比99203有所减小。

（2）当确定必抽5个最大单元时，均方误差减小的幅度最大，减小为18017。

（3）相比对极小值的处理，对极大值处理下的改进效果更为明显。

特别说明的是，如果不能确切的判断出哪些单元是极大值，假设是随机确定了k个单元作为必抽单元，在总体余下的N-k个单元中，再随机抽取n-k个单元进行调查，此时相当于直接在总体的N个单元中随机抽取n个单元[3]，该方法将是无益之举，与传统的简单随机抽样没有区别。

说明在实际应用中，当总体单元中存在极大值时，只有在能确切地判断出哪些单元是极大值的情况下，该方法才有很好的应用效果。

4 小结

极端值存在时，有极小值或极大值两种情况：

对于极小值，如果能通过相关信息确定若干个影响程度可以忽略不计的极小值单元，可以先把这些极小值单元剔除，再进行随机抽样，这样虽然带来了一定的偏差（不大），但可以减小抽样方差，使得总的均方误差可能减小，提高估计精度。

对于极大值，如果能通过相关信息确定若干个影响程度很大的极大值单元，可以先把这些极大值单元确定为必抽单元，再在余下的单元中进行随机抽样，在抽样推断中结合必抽单元和抽样单元进行估计，这种估计是无偏的，并且在一般情况下，都能使得总的均方误差减小，提高估计精度。

这种改进方法应用于有极端值存在并已知的情况下，事实上它已有着广泛的现实应用，比如在我国的企业调查中，一般对大企业进行普查（相当于对极大值进行必抽），对中小企业进行抽样调查。本文的意义在于明确的提出了对有极端值存在时随机抽样的改进方法，并论证和例证了该方法的优良性质和改进效果。

[1]金勇进，杜子芳，蒋妍.抽样技术（第二版）[M].北京：中国人民大学出版社，2008.

[2]卢宗辉等.抽样方法的比较研究[J].数量经济技术经济研究，2005,(4).

[3]艾小青，金勇进.样本追加——一个抽样技术难题的探析[J]，统计教育，2008,（11）.