一类积分微分方程的S-渐近ω-周期解

吴中华

(广州南洋理工职业学院 基础部，广东 广州 510925)

一类积分微分方程的S-渐近ω-周期解

吴中华

(广州南洋理工职业学院 基础部，广东 广州 510925)

研究了一类积分微分方程的S-渐近ω-周期温和解的存在性，通过利用S-渐近ω-周期函数性质结合不动点定理和强连续预解算子建立了一些S-渐近ω-周期温和解存在的充分条件。

S-渐近；ω-周期函数；积分微分方程；预解算子；温和解

在微分方程定性理论方面微分方程周期解的存在是最令人感兴趣和最重要的主题之一，又由于其在物理学、生物学、工程学、经济学、控制理论和其它领域有广泛的应用使其成为具有吸引力的主题。在现实中由于各种因素的影响，事物的变化往往呈现的结果不是完全周期的而是近似周期的。在过去几十年，很多种方程的好几种近似周期解的存在及其性质已有很多学者进行研究，例如：泛函微分方程、分数阶方程、积分微分方程的概周期(自守)、伪概周期(自守)、加权伪概周期(自守)等。S-渐近ω-周期是一种比渐近周期更一般的近似周期，S-渐近ω-周期摡念一经Henríquez等[1]首先提出,很多作者进行了进一步的研究[ 2-10]。在文献[11]中Dimbour利用Banach不动点定理研究了一类偏发展方程S-渐近ω-周期(温和)解存在的条件.在文献[12]中，Caicedo研究了如下抽象积分微分方程

(1)

x(0)=x0∈X

(2)

的S-渐近ω-周期(温和)解的存在性.在文献[13]中，Andrade研究了如下积分微分方程

(3)

x(0)=x0

(4)

的渐近周期存在性.其中在Banach空间X中，A:D(A)⊂X→X是闭线性稠定算子，{B(t)}t≥0是一族闭线性算子且对任意t≥0，D(B(t))⊇D(A).

本文在参考文献的基础上考虑积分微分方程(3)-(4)的S-渐近ω-周期温和解的存在性.

1 预备知识

文中假设方程(1)-(2)抽象柯西问题有一预解算子(参见文献[14]).

定义1[14]从X到X有界线性算子单参数族(R(t))≥0如果满足下列条件，则称为方程(1)-(2)的强连续预解算子

(1)R(0)=I(X上的恒等算子) 和对于任意x∈X在[0,∞)上函数R(t)x是连续的.

(2) 对于所有t≥0,R(t)D(A)⊆D(A)且x∈D(A),在[0,∞)上AR(t)x是连续的,且在[0,∞)上R(t)x是连续可微的.

(3)对于x∈D(A),下列预解方程成立,

定义2[13]函数u∈C([0,∞)，X) 称作方程(3)-(4) 的温和解，如果u(0)=x0且

文中Cb([0,∞)，X)表示从[0,∞)到Banach空间X的连续有界泛函的集合并赋予一致收敛范数‖·‖∞.

定义3[1]函数f∈Cb([0,∞)，X)称作S渐近周期的，如果存在ω>0使得 limt→∞(f(t+ω)-f(t))=0.这时称ω是f一个渐近周期，且f称为是S-渐近ω-周期的(记为f∈SAPω(X)).

定义4[1]一个连续函数f:[0,∞)×X→X若在X中的任意子集K，有{f(t,x):t≥0,x∈K}为有界且limt→∞(f(t+ω,x)-f(t,x))=0在x∈K是一致的.则称f在有界集上一致S-渐近ω-周期的.

引理1[1]设f:(-∞,0]×X→X在有界集是一致S-渐近ω-周期的和渐近一致连续.如果u:(-∞,0]→X是S-渐近ω-周期函数，那么函数v(t)=f(t,u(t))∈SAPω(X).

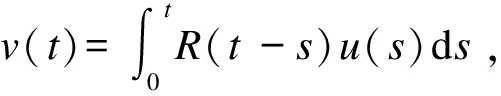
文中使用类似文献[15] 中一个公理化定义的相空间B,特别的B是一个泛函线性空间映(-∞,0]→X,满足一个半范数‖·‖B和以下公理：

(A) 如果x:(-∞,σ+a)|→X,a>0,σ∈R在[σ,σ+a) 上是连续的并且有xσ∈β，那么对于任意的t∈[σ,σ+a)以下条件成立:

(1)xt∈B；

(2) ‖x(t)‖≤H‖xt‖B；

(A1)x(·)为条件(A) 中定义的函数,xt在[σ,σ+a)上是B-值连续函数.

(B) 空间B是完备的.

(C) 如果(ψn)n∈N是一致有界连续函数序列并且支撑集为紧集,在紧的开拓扑下ψn→ψ,n→∞,则ψ∈B以及‖ψn-ψ‖B→0当n→∞.

注1：因为B满足条件(C),所以空间Cb((-∞,0],X)由所有连续有界泛函ψ:(-∞,0]→X构成，并连续嵌入空间B.因此，存在一个常数L≥0使得‖ψ‖B≤L‖ψ‖∞，对于任意的ψ∈Cb((-∞,0],X).(参见文献[15]命题7.1.1)

定义5 设S(t):B→B是C0- 半群,当[-t,0] 时,S(t)φ(θ)=φ(0);当(-∞,-t] 时,S(t)φ(θ)=φ(t+θ),如果对任意φ∈B且φ(0)=0，当t→∞时,‖S(t)φ‖B→0.称相空间B是衰退记忆空间.

注2：文中假设存在常数K>0使得max{K(t),M(t)}≤K对所有的t≥0，显然此条件是可以验证的.(参见文献[15]命题7.1.5)

2 主要结果

(H1) 预解算子(R(t))≥0是一致指数稳定，对于全体t≥0和常数M,δ>0有‖R(t)‖≤Me-δt.

(H2)函数f,g:R+×B→X在有界集是一致S-渐近ω-周期，使得

‖f(t,ψ1)-f(t,ψ2)‖X≤Lf‖ψ1-ψ2‖B

‖g(t,ψ1)-g(t,ψ2)‖X≤Lg‖ψ1-ψ2‖B

对所有(t,ψi)∈[0,∞)×B,i=1,2成立.

(H3)函数f,g:R+×B→X在有界集是一致S-渐近ω-周期，假设存在连续非递减函数Lf,Lg:[0,∞)→[0,∞)使得对于每个正数 R 和ψ1,ψ2∈B,‖ψ1‖B≤R,‖ψ2‖B≤R有‖f(t,ψ1)-f(t,ψ2)‖X≤Lf(R)‖ψ1-ψ2‖B，

‖g(t,ψ1)-g(t,ψ2)‖X≤Lg(R)‖ψ1-ψ2‖B

对所有t∈R+成立，这里对每个t≥0，有Lf(0)=Lg(0)=0 ，f(t,0)=g(t,0)=0 .

在下述结果中，l在从X到X上，L是一个常数.(见注1)

定理1 设B是衰退记忆空间且条件(H1)-(H2) 成立，若LLf‖l‖L(X,X)<1，则方程(3)-(4)存在唯一的S-渐近ω-周期温和解.

证明：设SAPω,0(X)={x∈SAPω(X)|x(0)=0}.很清楚 ,SAPω,0(X)是SAPω(X) 的闭子空间.对于θ≤0，通过x(θ)=0确定x∈SAPω,0(X)扩展至R. 用符号y(·) 来表示y0=φ和y(t)=R(t)φ(0)， 对t≥0 .通过

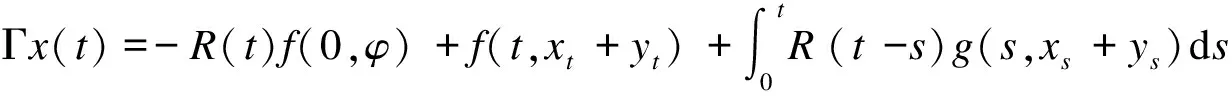
(5)

在SAPω,0(X)上定义映射Γ.从假设和引理2可知Γ是从SAPω,0(X)到SAPω,0(X)的映射.而且从

(6)

可判断出Γ是连续的.

另一方面，通过

Λα(t)=LLf‖l‖L(X,X)α(t)+

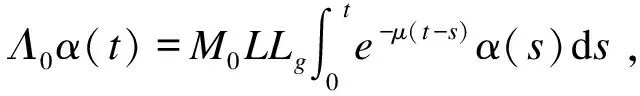
m(Γx-Γz)≤Λm(x-z) ，

运用(文献[16]定理1) ，可以得出Γ有唯一固定点x∈SAPω,0(X).规定u(t)=y(t)+x(t) ，对于t∈R，可以得出u∈SAPω(X)是方程(3)-(4)的唯一温和解.

定理2 设B是衰退记忆空间且条件(H1)和(H3) 成立，若存在ε>0使得对每一个φ满足‖φ‖B<ε，则方程(3)-(4)存在唯一的S-渐近ω-周期温和解.

证明：设R>0 ，λ∈(0,1) 且有

这里K是常数[见注2].证实对于ε=λR成立.实际上若φ满足‖φ‖<ε， 通过x0=0确定x∈SAPω,0(X)扩展至R 且定义空间DR:={x∈SAPω,0(X):‖x‖∞≤R}，赋予度量d(u,v)=‖u-v‖∞.在空间DR上通过(Γx)0=0和(5)定义算子 Γ .设x在DR内，应用定理1相似的证明方法可得Γx∈SAPω,0(X).而且有

‖(Γx)(t)‖≤Lf(1+(MH+1)λ)

因此Γ(DR)⊂DR.在另一方面x,z∈DR，可得

这证明了Γ是一个从DR到DR的压缩映射.这一结论是从Banach不动点定理得出的结果.

3 结束语

文章通过利用S-渐近ω-周期函数性质并且结合不动点定理和强连续预解算子得到了积分微分方程(3)-(4)的S-渐近ω-周期温和解存在的充分条件。

[1] Henríquez H R,Pierri M,Táboas P.On S-asymptotically ω-periodic functions on Banach spaces and applications[J].Journal of Mathematical Analysis and Applications,2008,343(2):1119-1130.

[2]Cuevas C,César de Souza J.Existence of S-asymptotically ω-periodic solutions for fractional order functional integro-differential equations with infinite delay[J].Nonlinear Analysis:Theory,Methods & Applications,2010,72(3):1683-1689.

[3]Cuevas C,de Souza J C.S-asymptotically ω-periodic solutions of semilinear fractional integro-differential equations[J].Applied Mathematics Letters,2009,22(6):865-870.

[4]Henriquez H R,Pierri M,Táboas P.Existence of S-asymptotically ω-periodic solutions for abstract neutral equations[J].Bulletin of the Australian Mathematical Society,2008,78(3):365-382.

[5]De.Andrade B,Cuevas C.S-asymptotically ω-periodic and asymptotically ω-periodic solutions to semi-linear Cauchy problems with non-dense domain[J].Nonlinear Analysis:Theory,Methods & Applications,2010,72(6):3190-3208.

[6]Cuevas C,Lizama C.S‐asymptotically ω‐periodic solutions for semilinear Volterra equations[J].Mathematical Methods in the Applied Sciences,2010,33(13):1628-1636.

[7]Pierri M.On S-asymptotically ω-periodic functions and applications[J].Nonlinear Analysis:Theory,Methods & Applications,2012,75(2):651-661.

[8]Blot J,Cieutat P,N'Guérékata G M.S-asymptotically ω-periodic functions and applications to evolution equations[J].African Diaspora Journal of Mathematics,New Series,2011,12(2):113-121.

[9] Pierri M.S-asymptotically ω-periodic functions on Banach spaces and applications to differential equations[C].Sao Paulo :Universidade de sao Paulo,2009.

[10]Caicedo A,Cuevas C,Mophou G M,et al.Asymptotic behavior of solutions of some semilinear functional differential and integro-differential equations with infinite delay in Banach spaces[J].Journal of the Franklin Institute,2012,349(1):1-24.

[11]Dimbour W,N’Guérékata G M.S-asymptotically ω-periodic solutions to some classes of partial evolution equations[J].Applied Mathematics and Computation,2012,218(14):7622-7628.

[12]Caicedo A,Cuevas C,Henríquez H R.Asymptotic periodicity for a class of partial integrodifferential equations[J].ISRN Mathematical Analysis,2011,(1):1-18.

[13]Andrade B,Cuevas C,Henríquez E.Asymptotic periodicity and almost automorphy for a class of Volterra integro-differential equations[J].Mathematical Methods in the Applied Sciences,2012,35(7):795-811.

[14]Diagana T,Hernández M E,Dos Santos J P C.Existence of asymptotically almost automorphic solutions to some abstract partial neutral integro-differential equations[J].Nonlinear Analysis:Theory,Methods & Applications,2009,71(1):248-257.

[15]Hino Y,Naito T,Murakami S.Functional differential equations with infinite delay[M].Berlin :Springer,1991.

[16]Henriquez H R.Approximation of abstract functional differential equations with unbounded delay[J].Indian Journal of Pure and Applied Mathematics,1996,(27):357-386.

(责任编辑：马金发)

S-asymptoticallyω-periodic Solutions of Integrodifferential Equations

WU Zhonghua

(Basis Course Department Guangzhou Nanyang Polytechnic，Guangzhou 510925，China)

Existence ofS-asymptoticallyω-periodic mild solutions for a class integrodifferential equation is considered.Some sufficient conditions are established by using properties ofS-asymptoticallyω-periodic function combined with Banach fixed point theorem and strongly continuous family of resolvent operators.

S-asymptotically;ω-periodic function;integrodifferential equation;resolvent operator;mild solution

2014-08-25

吴中华(1975— ), 男, 讲师，研究方向: 泛函方程.

1003-1251(2015)03-0075-04

O175

A