半严格凸函数的性质及应用

李艳

（延安职业技术学院，陕西延安716000）

半严格凸函数的性质及应用

李艳

（延安职业技术学院，陕西延安716000）

凸函数是一类重要的函数，它在凸分析和数学规划等学科中扮演着主要的角色，在不等式证明方面及其它各领域有着广泛的应用。本文在杨新民对半严格凸函数研究的基础上，给出了半严格上凸函数和半严格下凸函数的一些性质，研究了它们在不等式证明中的应用，并给出了若干例子。

半严格凸函数；性质；不等式；应用

一、引言

凸函数是凸分析中研究的主要内容，它在数理经济、工程、管理科学及优化理论中有广泛应用，特别是在数学规划的各个分支中经常涉及到凸函数。文献[1-5]中给出了上（下）凸函数，严格上（下）凸函数的定义和性质。文献[7-10]中给出了凸函数及严格凸函数在积分不等式中的应用。杨新民在文献[6]中给出半严格凸函数的定义，并讨论了凸函数、半严格凸函数和严格凸函数之间的关系。

本文对半严格凸函数作了进一步研究和讨论。在预备知识中给出半严格上（下）凸函数的定义,在主要结果中给出半严格上（下）凸函数的一些性质,研究它们在不等式证明中的应用,并给出若干例子。这在一定意义上推广和完善了半严格凸函数。

二、预备知识

定义1[1]设函数ƒ（x）在区间[a,b]上连续,若对任意x1，x2∈[a,b],以及任意λ∈（0，1）,有

则称ƒ（x）为[a,b]上的凸函数.

定义2[1]设函数ƒ（x）在区间[a,b]上连续,若对任意x1，x2∈[a,b],以及任意λ∈（0，1）,有

则称为[a,b]上的严格凸函数.

定义3[1]设函数ƒ（x）在区间[a,b]上连续,若对任意x1，x2∈[a,b],以及任意λ∈（0，1）,有

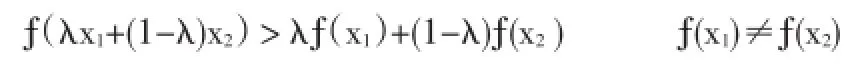
则称ƒ（x）为[a,b]上的半严格凸函数.

注：定义1[1[1]中不等式符号反向,则称ƒ（x）为[a,b]上的半严格上凸函数。在下文中我们主要讨论半严格上凸函数和半严格下凸函数的性质及应用。

三、主要结果

现在我们提出半严格上凸函数和半严格下凸函数的一些性质。

定理1设ƒ（x）在区间[a,b]上的半严格上凸函数,则对于任意的a∈[0,1]（或a∈[-1,0]）有,aƒ（x）在[a,b]上是半严格上(下)凸函数.

直接由定义可证.

定理2设ƒ（x）,g（x）在区间[a,b]上是半严格上凸函数,则ƒ（x）+g（x）在[a,b]上也是半严格上凸函数.

证明ƒ（x）,g（x）在区间[a,b]上是半严格上凸函数,对任意x1，x2∈[a,b]有

从而

因此h（x）是半严格上凸函数,即ƒ（x）+g（x）在[a,b]上是半严格上凸函数.

定理3 1。若ƒ（u）是半严格上凸且单调增加的函数,g（x）是半严格上凸函数,则ƒ(g（x）)也是半严格上凸函数.

2。若ƒ（u）是半严格下凸且单调减少的函数,g（x）是半严格上凸函数,则ƒ(g（x）)是半严格下凸函数.

3。若ƒ（u）是半严格下凸且单调增加的函数,g（x）是半严格下凸函数,则ƒ(g（x）)是半严格下凸函数.

4。若ƒ（u）是半严格上凸且单调减少的函数,g（x）是半严格下凸函数,则ƒ(g（x）)是半严格上凸函数.

证明1。g（x）是半严格上凸函数,则有

而ƒ（u）是半严格上凸且单调增加的函数,因此

故ƒ(g（x）)是半严格上凸函数.

同理可证性质2。-4。.

由性质3。可得

1。若ƒ（x）是半严格下凸函数,则eƒ（x）也是半严格下凸函数.

2。若ƒ（x）是半严格上凸函数,则Inƒ（x）也是半严格上凸函数.

进一步可得

esinx在[2kπ,2kπ+2π](k=0,±1,±2…)是半严格下凸函数；

Insinx在[2kπ,2kπ+2π](k=0,±1,±2…)上是半严格上凸函数.

定理4 1。设y=ƒ（x）是半严格上凸且严格增加函数,则其反函数x=ƒ-1（y）是半严格下凸严格增加函数.

2。设y=ƒ（x）是半严格上凸且严格减少函数,则其反函数x=ƒ-1（y）是半严格上凸严格减少函数.

3。设y=ƒ（x）是半严格下凸且严格增加函数,则其反函数x=ƒ-1（y）是半严格上凸严格增加函数.

4。设y=ƒ（x）是半严格下凸且严格减少函数,则其反函数x=ƒ-1（y）是半严格下凸严格减少函数.

证明1。y=ƒ（x）是严格增加函数,则其反函数x=ƒ-1（y）也是严格增加函数.由y=ƒ（x）是半严格上凸函数,有

即ƒ-1(y)是半严格下凸且严格增加的函数.

同理可证性质2。-4。.

下面我们给出半严格凸函数的一些应用.先介绍Jensen不等式然后考虑在证明积分不等式方面的应用.

例1（Jensen不等式）设ƒ（x）为[a,b]上的半严格上凸函数.t1＞0（i=1,2,…，n）且则

证明对n采用数学归纳法.

当n=2时,有

即为半严格上凸函数的定义.

设结论对于n≤k-1时成立,下面证明n=k时结论也成立.

由数学归纳法知,结论成立.

例2设ƒ（x）,g（x）在区间[a,b]上可积,且m≤ƒ（x）≤M，g（x）≥0,及∫bg（x）dx＞0，R（t）,R(t)在[m,M]上是半严格上凸函数,则

证明ƒ（x）,g（x）在区间[a,b]上可积,因此无论对[a,b]作怎样的分割,其积分和的极限存在且相等.对[a,b]作n等分,并设

考虑到R(t)为半严格上凸函数及

例3设ƒ（x）,g（x）是[a,b]上的正值连续函数,g（x）非常数,则

证明利用例2的结论.

1。设R（t）=-et,则R（t）是半严格上凸函数

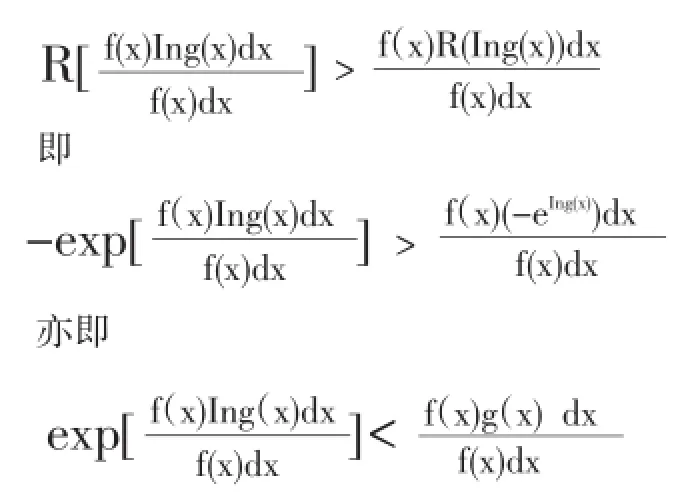
2。设Q（t）=-et,则Q（t）是半严格上凸函数.仿1。之证法，即可得

O174.13

A

1674-6198（2015）03-0076-03

2015-05-12

李艳（1986－）女，陕西佳县人，延安职业技术学院教师。