分数阶脉冲微分方程组边值问题解的存在性

江卫华，李海明

(河北科技大学理学院，河北石家庄 050018)

1 问题提出

分数阶微分方程的出现已有300多年历史，由于其理论的自身发展以及在流变学、电子网络、黏弹性、物理化学、分析化学、生物学和控制理论等学科中的广泛应用，使得分数阶微分方程受到越来越多学者的广泛关注［1-21］。

文献［1］研究了非线性脉冲微分方程边值问题:

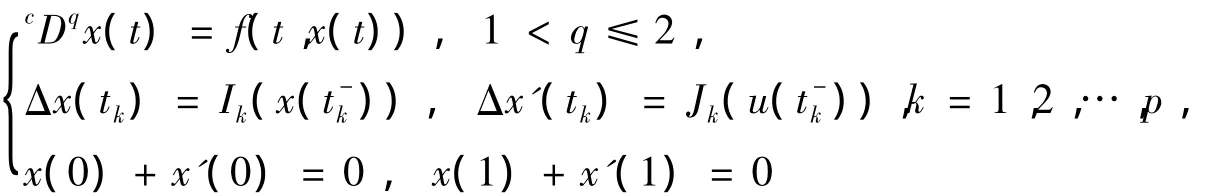
解的存在性。

受上述文献的启发，本文研究如下非线性脉冲微分方程组边值问题:

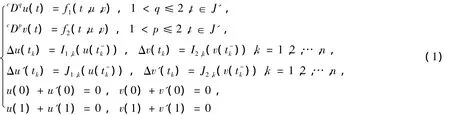
解的存在性。其中

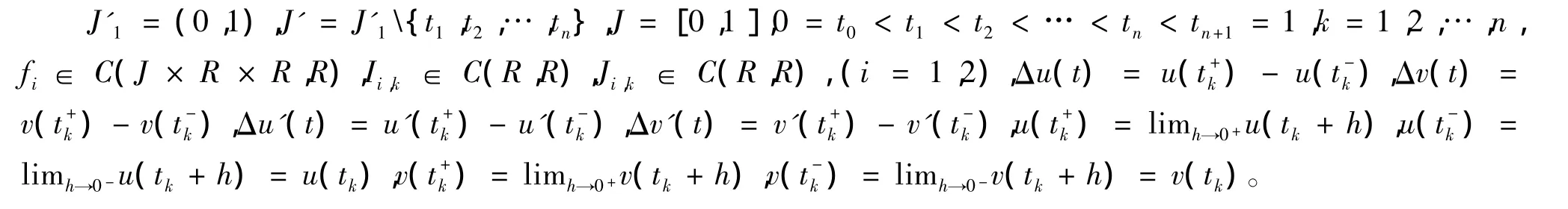
2 预备知识

定义1［1］函数u定义在区间(0，1)，q＞0，则阶数为q的Riemann-Liouville分数阶积分定义为

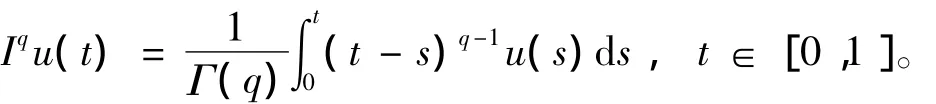
定义2［1］函数u定义在区间(0，1)，q＞0，则阶数为q的Riemann-Liouville分数阶导数定义为

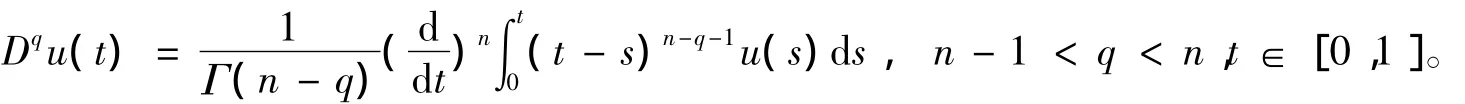
取空间

PC(J，R)={x:J→R;x∈C((tk，tk+1］，R)，k=0，1，2，…，n，x)=x(tk)，k=1，2，…，n}，范数为‖x‖PC=supt∈J|x(t)|。

PC1(J，R)={x'∈PC(J，R);x'()=x'(tk)，k=1，2，…，n)， 范 数 为 ‖x‖PC1=max{‖x‖PC，‖x'‖PC}。

由文献［1］知PC(J，R)及PC1(J，R)是 Banach空间。乘积空间PC1(J，R)×PC1(J，R)，范数定义为‖(u，v)‖=max{‖u‖PC1，‖v‖PC1}，∀(u，v)∈PC1(J，R)×PC1(J，R)，是一个 Banach 空间。

定理1［1］(压缩映像原理)设X是完备的度量空间，T是X上的压缩映像，那么T有且只有一个不动点。

定理2［1］(krasnoselskii不动点定理)设M是Banach空间X中的一个非空凸子集。假设A，B是2个映射，使得:

1)对任意的x，y∈M，有Ax+By∈M;

2)A是全连续映射;

3)B是一个压缩映射，则存在至少一个z∈M，使得z=Az+Bz。

引理1［1］假设

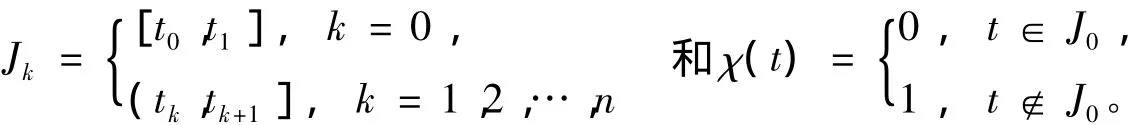
对于φ，ζ∈C［0，1］则分数阶脉冲微分方程组边值问题:

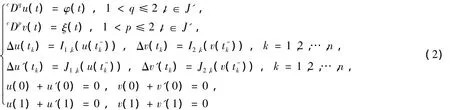
的解为(u(t)，v(t))。其中

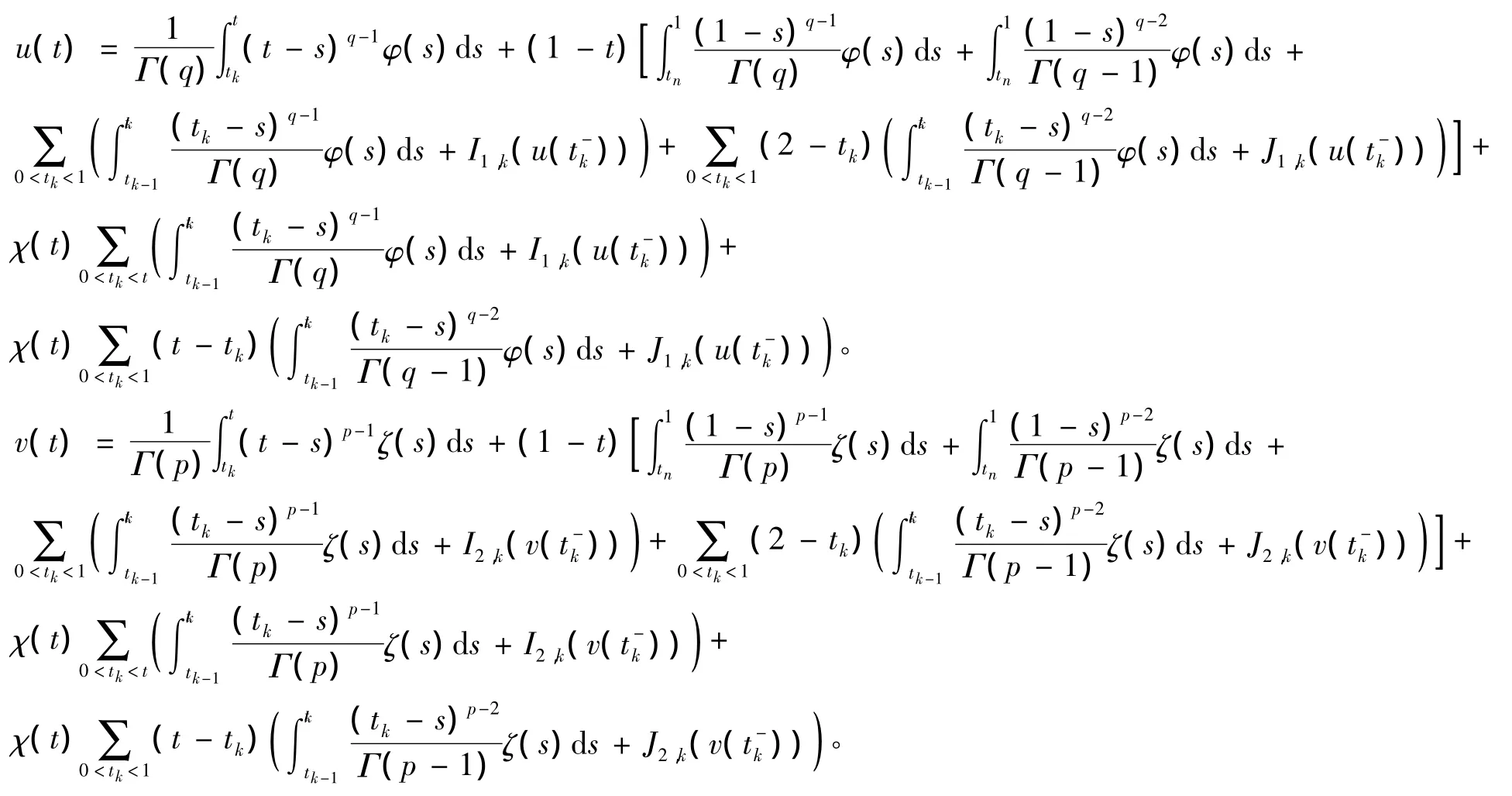
3 主要结果

定理 3 令fi∈C(J×R×R，R)，Ii，k∈C(R，R)，Ji，k∈C(R，R)，(i=1，2)，fi是连续有界函数，Ii，k，Ji，k是连续函数。假如存在正实数L1，L2，L3，M2，M3，l1，l2，l3，m2，m3使得:

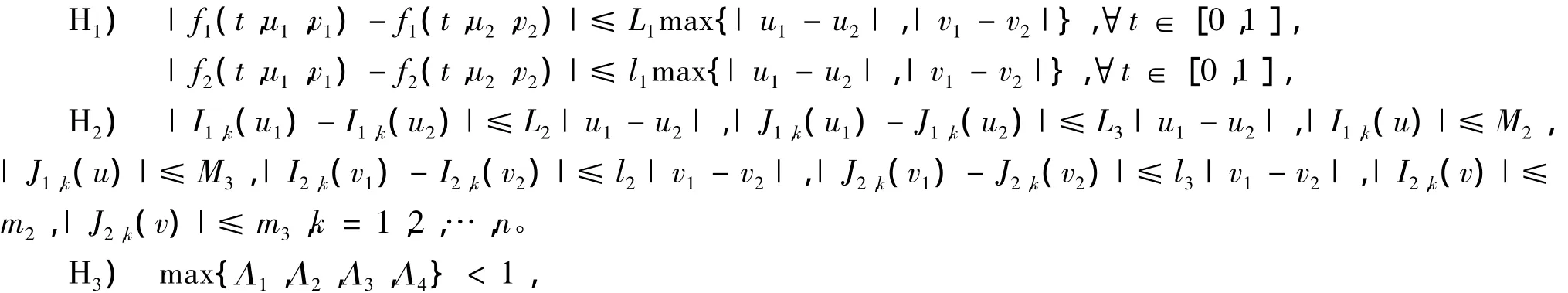
其中

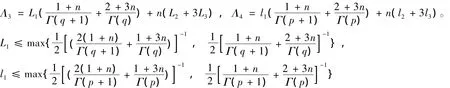
成立，则分数阶脉冲微分方程组(1)在PC1(J，R)×PC1(J，R)中有唯一解。

证明 定义映射A:PC1(J，R)×PC1(J，R)→PC1(J，R)×PC1(J，R)如下:

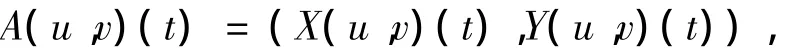
其中:

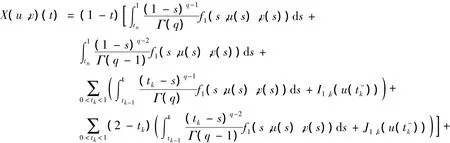
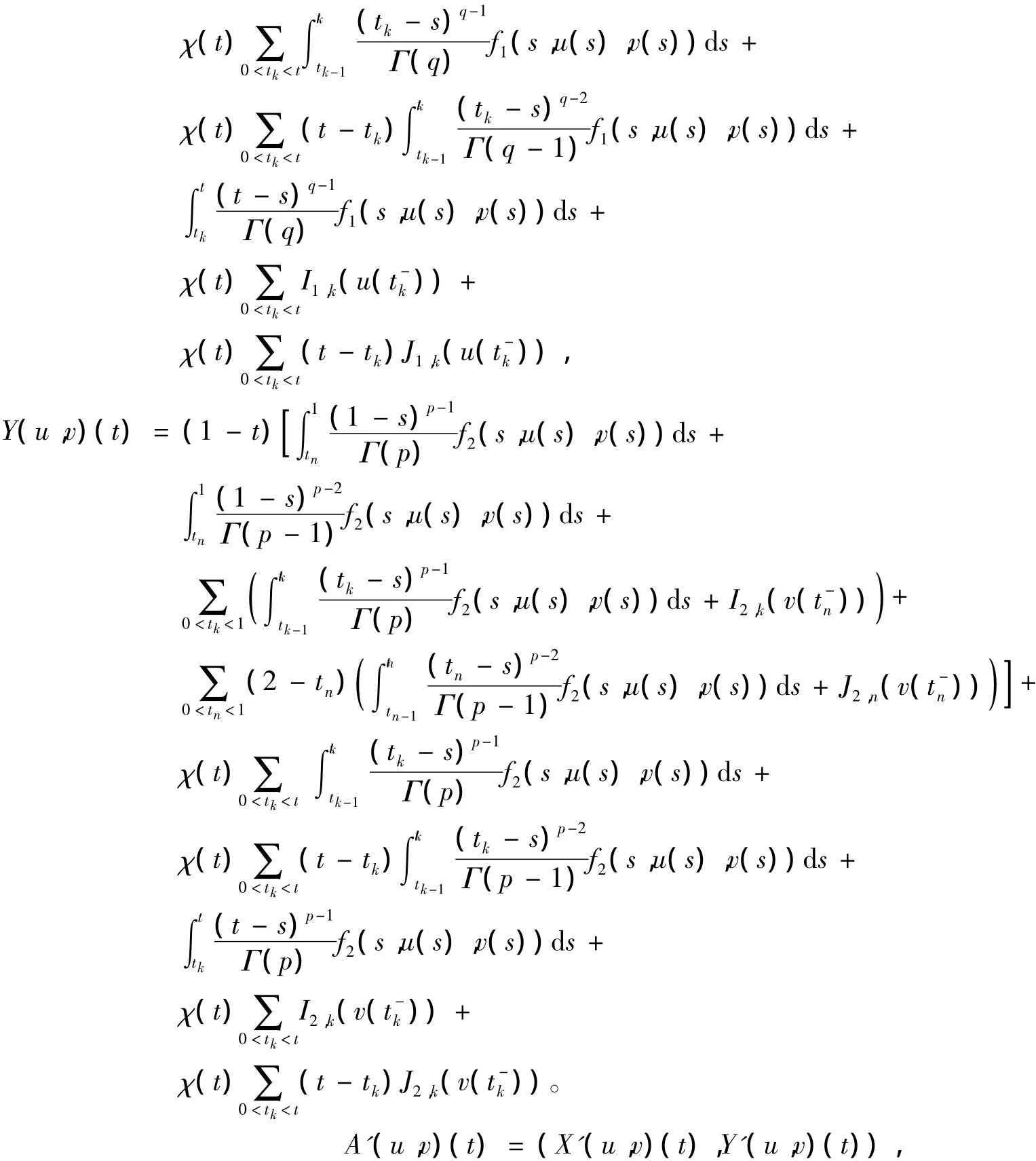
其中:

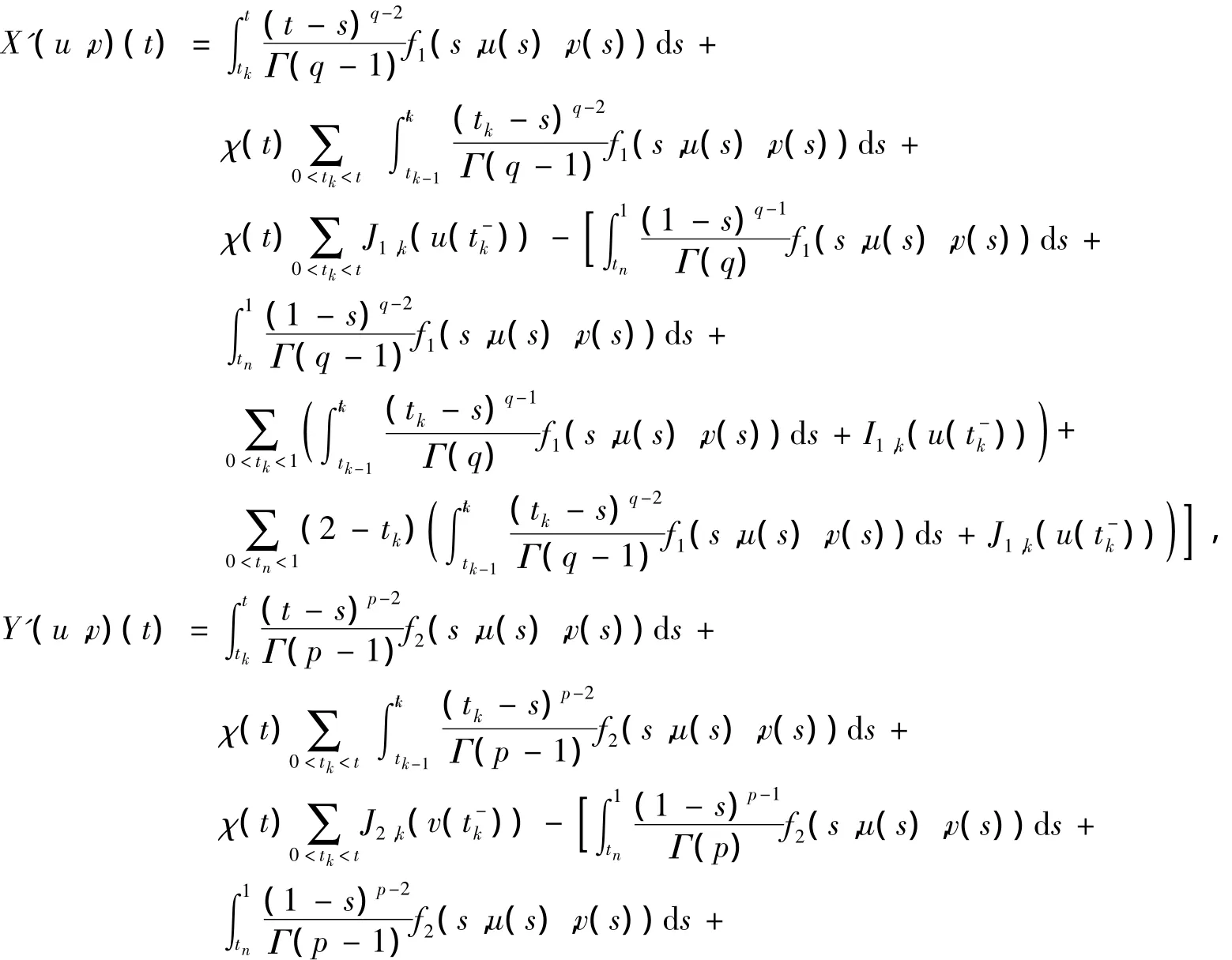
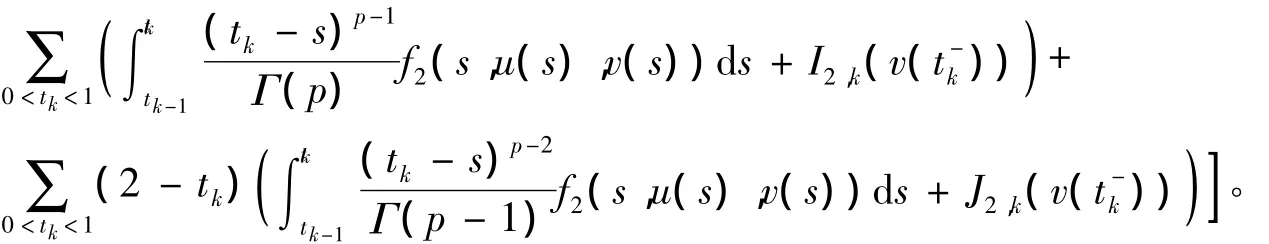
定义 s upt∈［0，1］|f1(t，0，0)|=M1，supt∈［0，1］|f2(t，0，0)|=m1。取

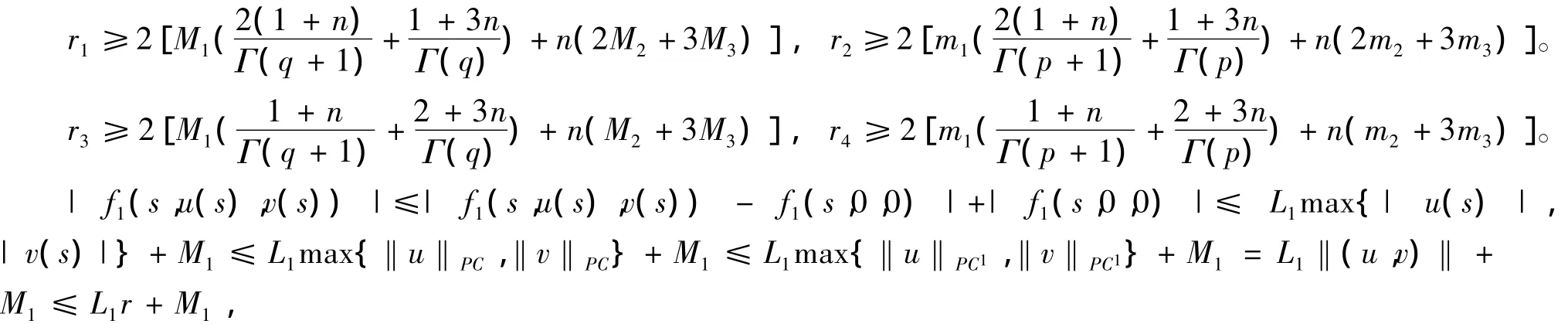
其中r=max{r1，r2，r3，r4}，

下面需要证明A(Br)⊂Br，其中Br={(u，v)∈PC1(J，R)×PC1(J，R):‖(u，v)‖PC1≤r}。

对于(u，v)∈Br有

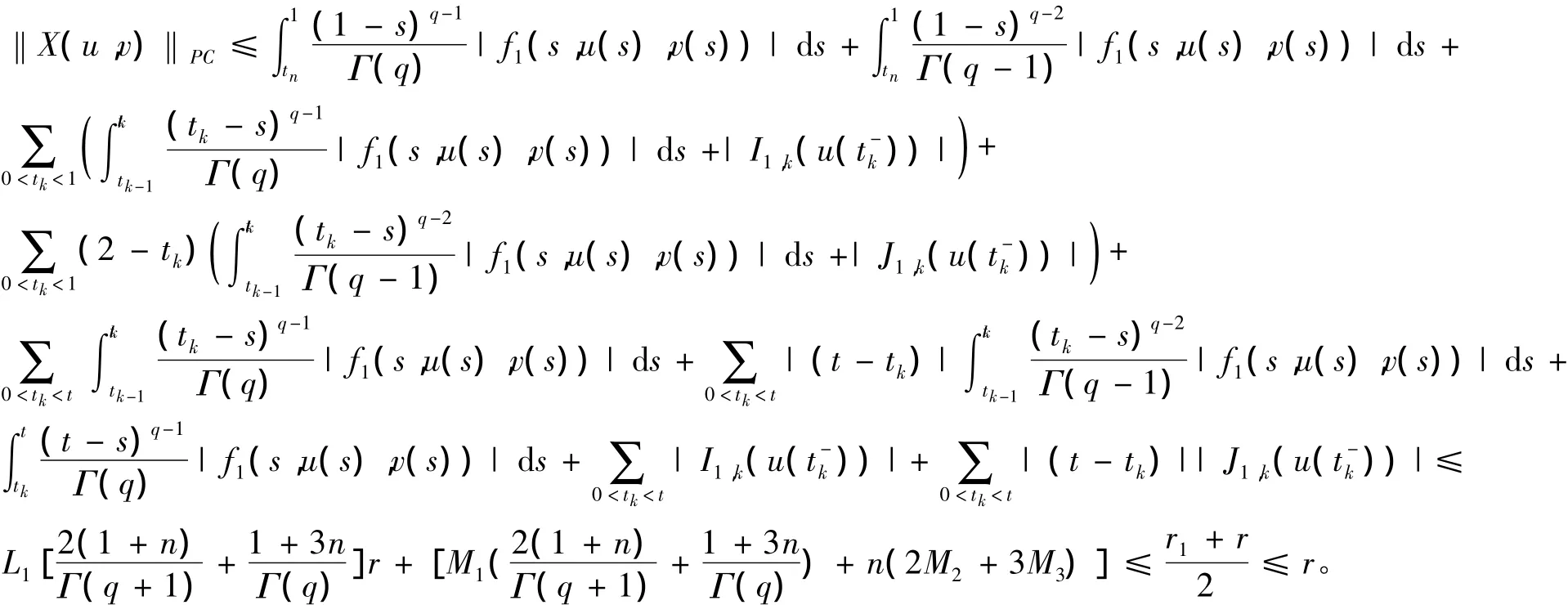
类似可得:

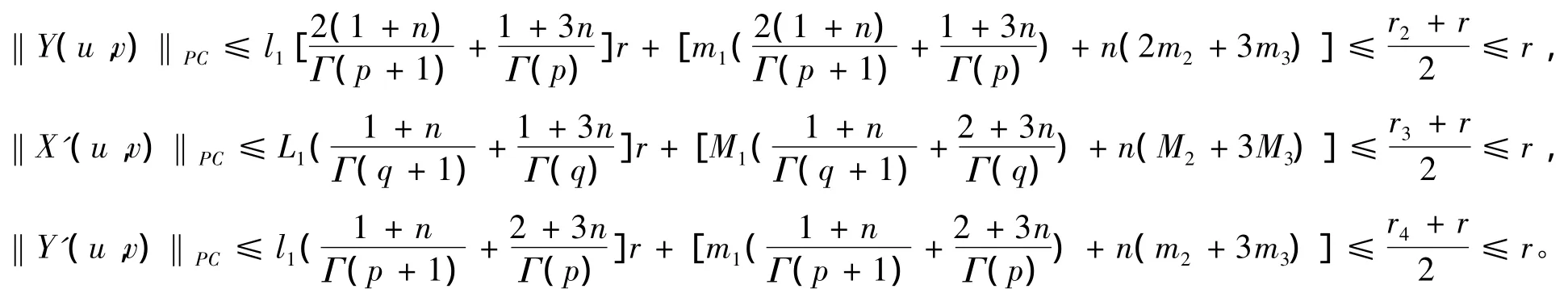
所以有:

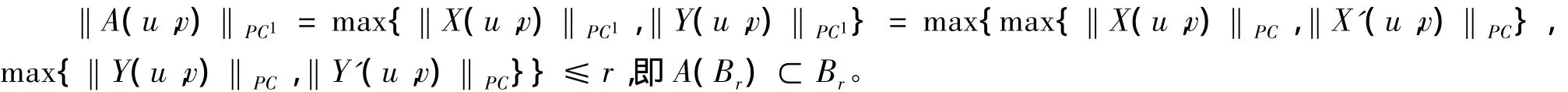
再证A:Br→Br是压缩映像。

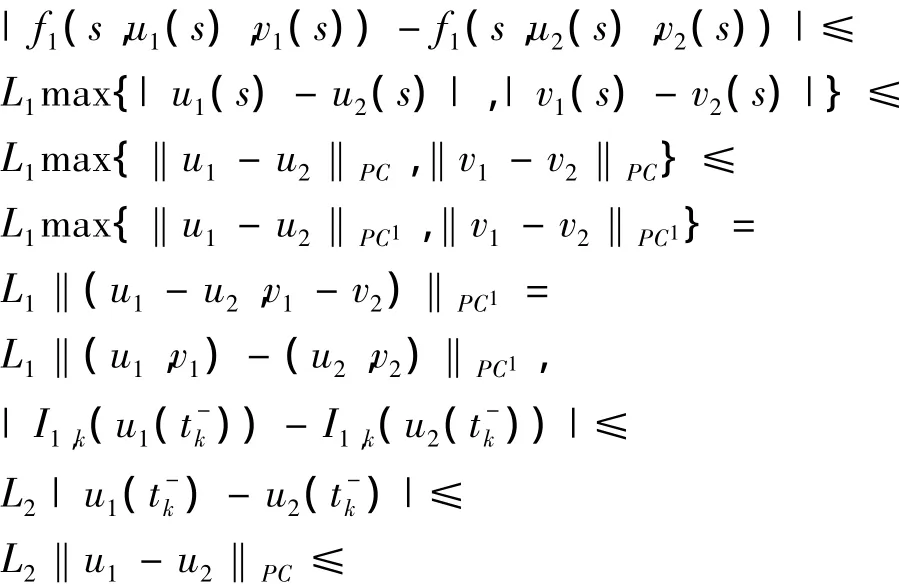
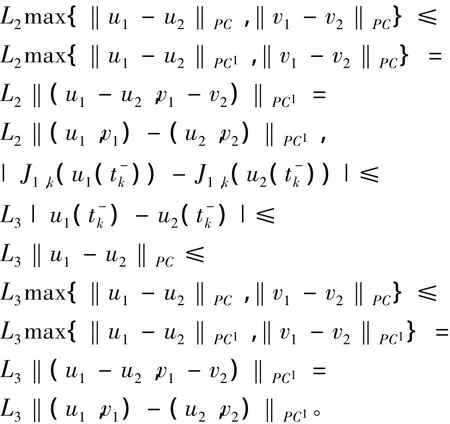
对于(u1，v1)，(u2，v2)∈PC1(J，R)×PC1(J，R)，∀t∈［0，1］，有:

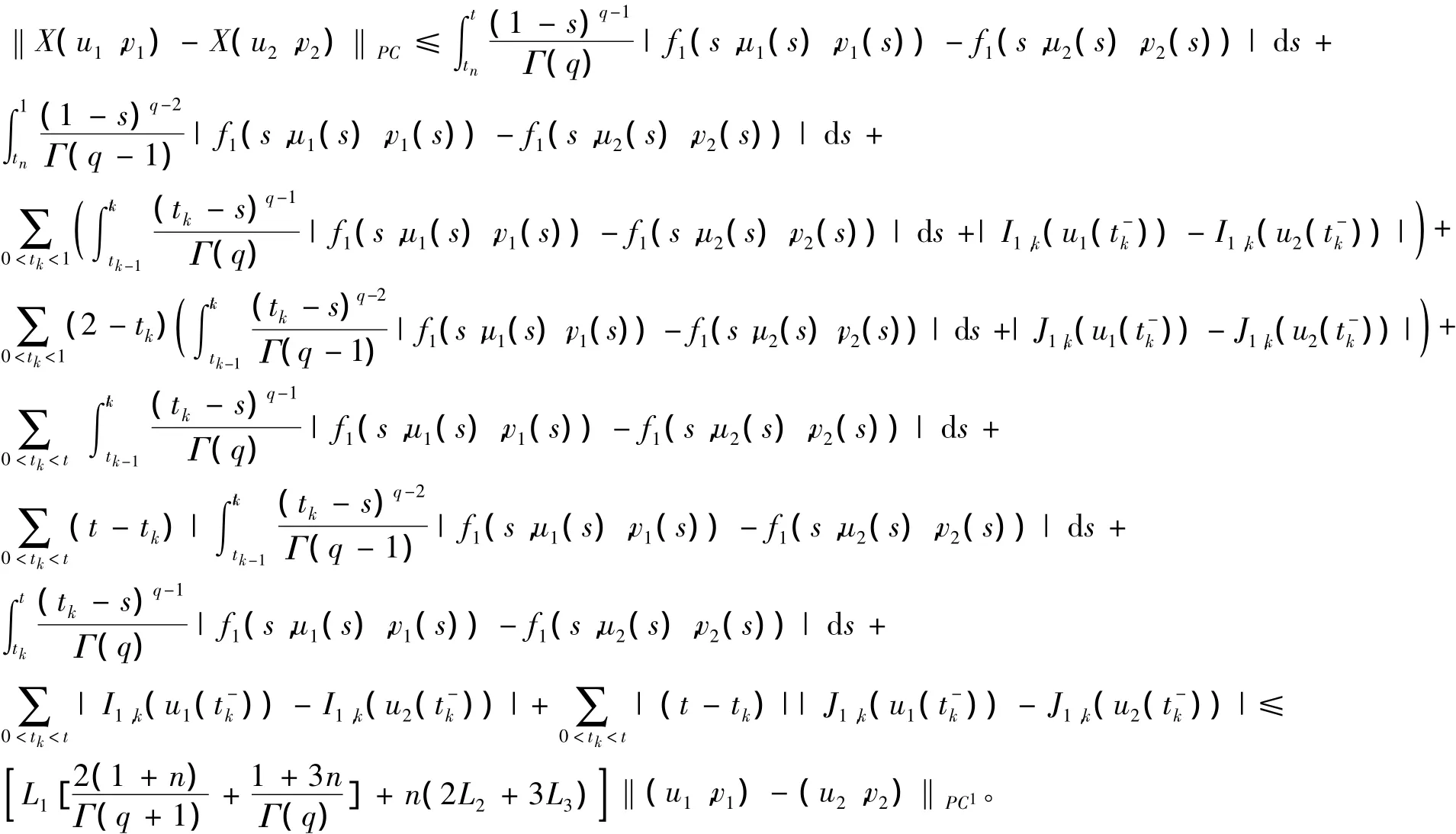
类似可得:

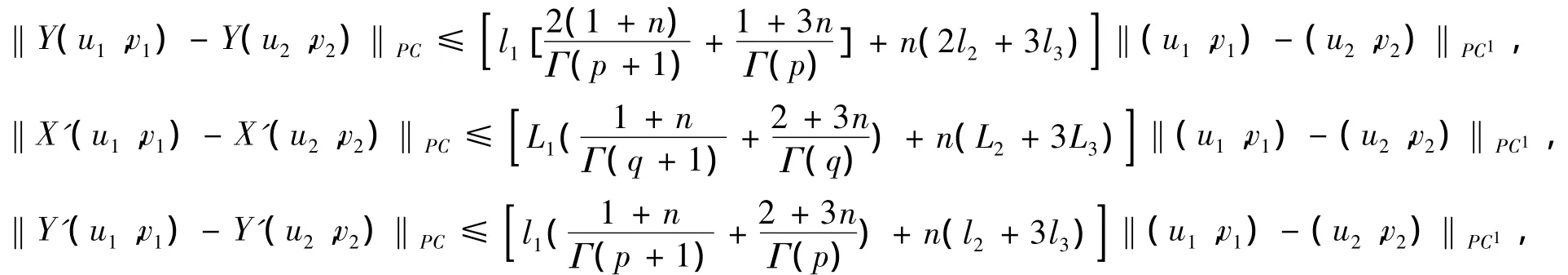
则有:

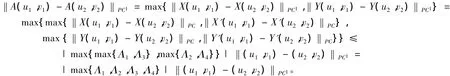
其中:

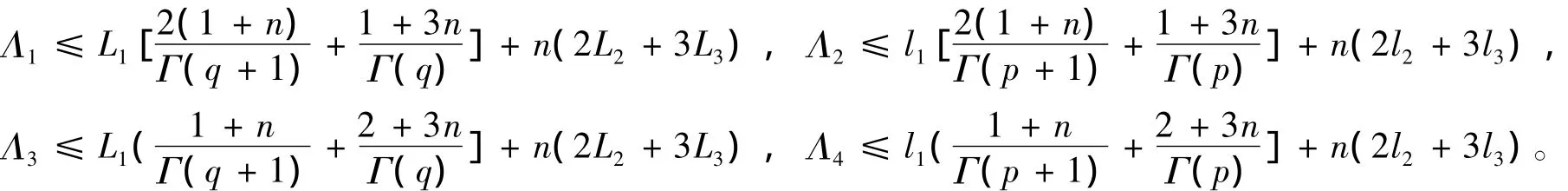
由于max{Λ1，Λ2，Λ3，Λ4}＜1，则表明A(u，v)(t)是一个压缩映射，因此，根据压缩映像原理定理得证。

定理4 如果条件H1)和条件H2)成立，且n(2L2+3L3)＜，对于 ∀ (t，u，v)∈［0，1］×R×R，有|fi(t，u，v)|≤ ‖μ‖L，i=1，2，其中 μ ∈L(［0，1］，R+，R+)。则边值问题(1)在［0，1］中至少有1个解。

证明 令

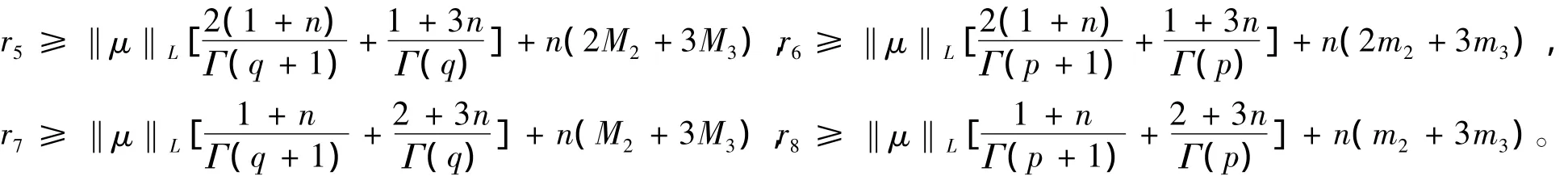
Br={(u，v)∈PC1(J，R)×PC1(J，R):‖(u，v)‖ ≤r}。(r=max{r5，r6，r7，r8})。定义在Br上的映射Φ和Ψ如下:

Φ(u，v)(t)=(Φ1(u，v)(t)，Φ2(u，v)(t))，其中

Ψ'(u，v)(t)=(Ψ'1(u，v)(t)，Ψ'2(u，v)(t))，其中

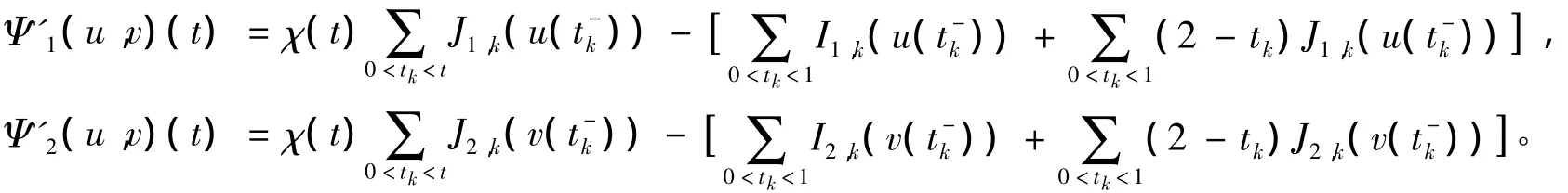
对于(u1，v1)，(u2，v2)∈Br，有

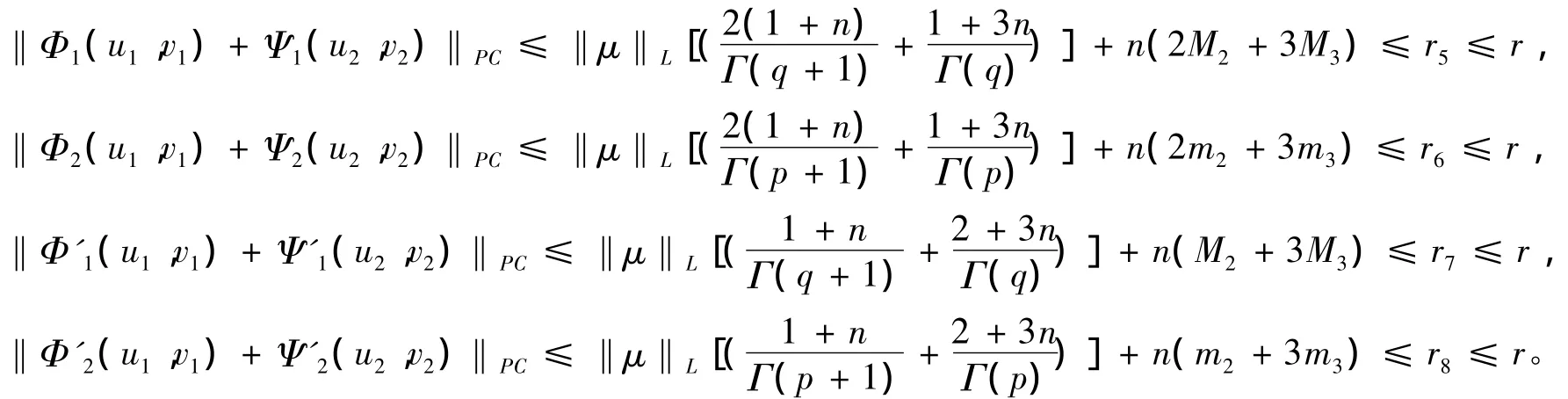
所以

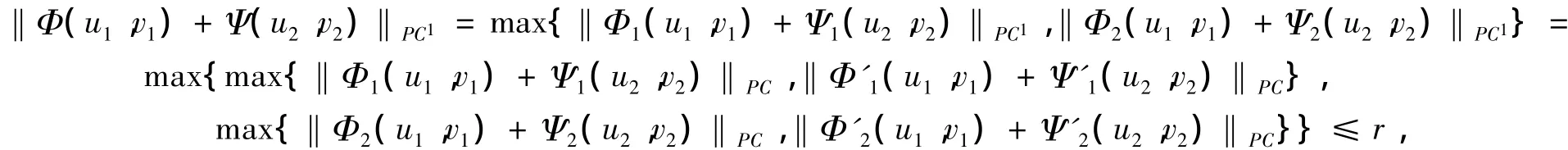
即 Φ(u1，v1)(t)+Ψ(u2，v2)(t)∈Br。

因为

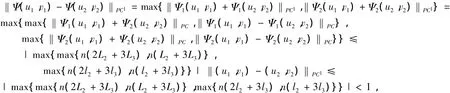
所以映射Ψ是压缩映射。

因为fi是连续有界函数，所以映射Φ是连续的，并且在Br上有界。

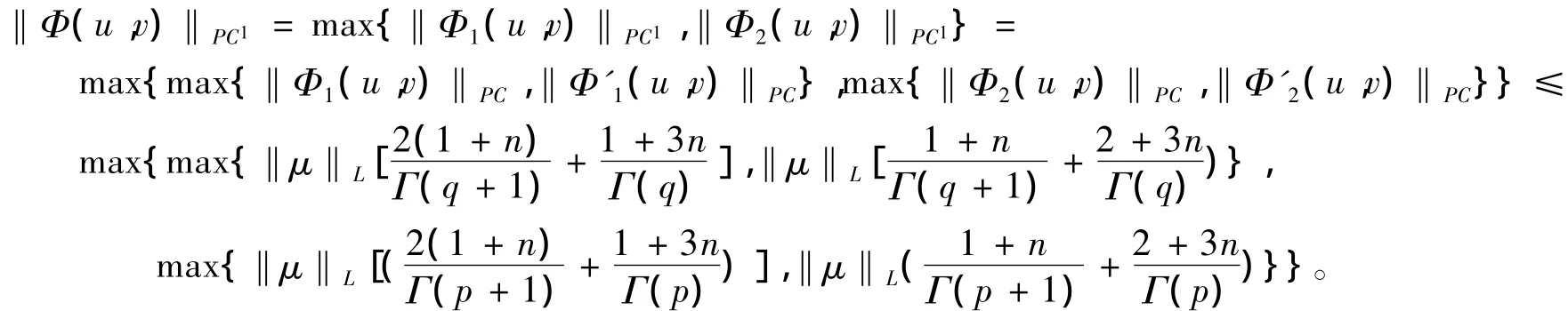
证明映射Φ的紧性。

令Ω=［0，1］×Br，定义sup(t，u，v)∈Ω|f1(t，u，v)|=f1max，sup(t，u，v)∈Ω|f2(t，u，v)|=f2max。

取 τ1，τ2∈［0，1］，τ1＜τ2，则有:

‖Φ1(u，v)(τ2)－Φ1(u，v)(τ1)‖PC=

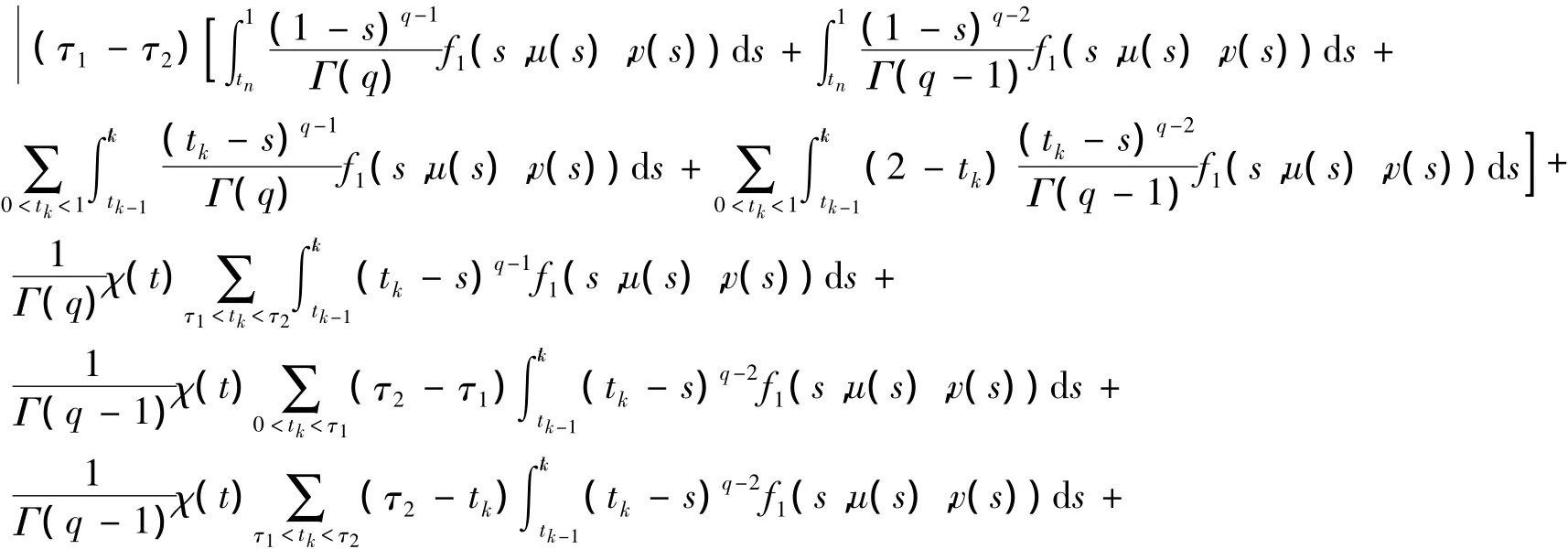
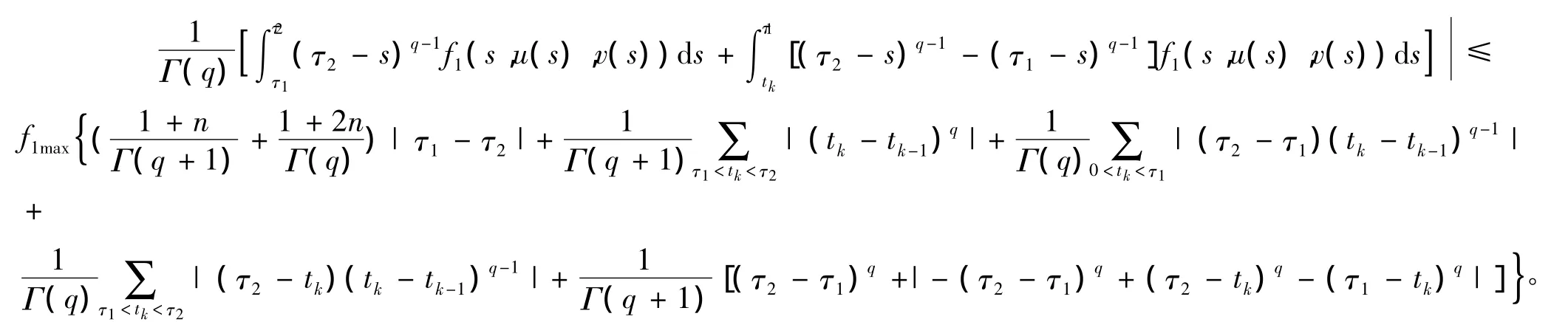
类似可得，

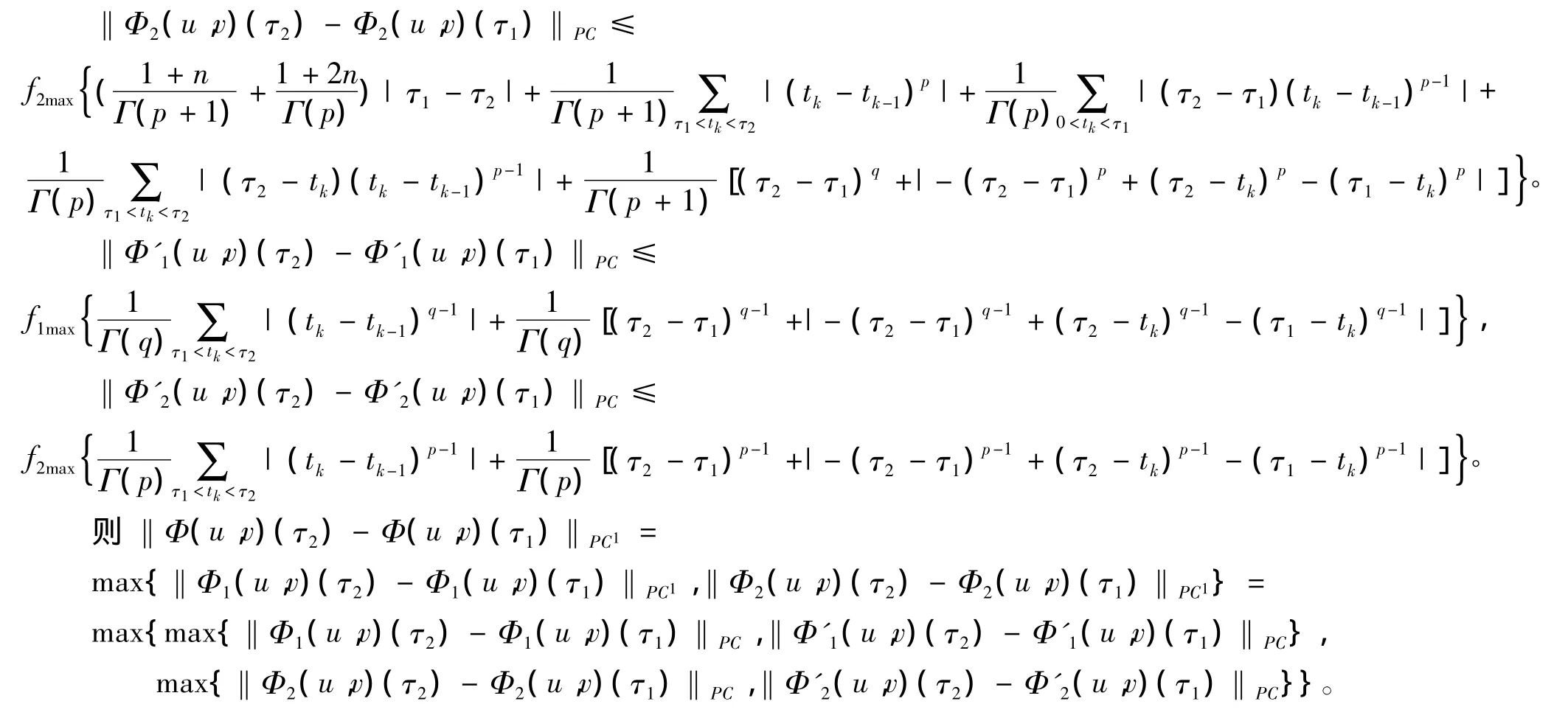
与(u，v)无关，则Φ在Br上是相对紧的。因此，由Arzela-Ascoil定理可知，Φ在Br上是紧的，则Φ是全连续的。所以满足定理3的所有条件，则边值问题(1)在［0，1］中至少有1个解。

4 举 例

例1 考虑分数阶脉冲微分方程组边值问题

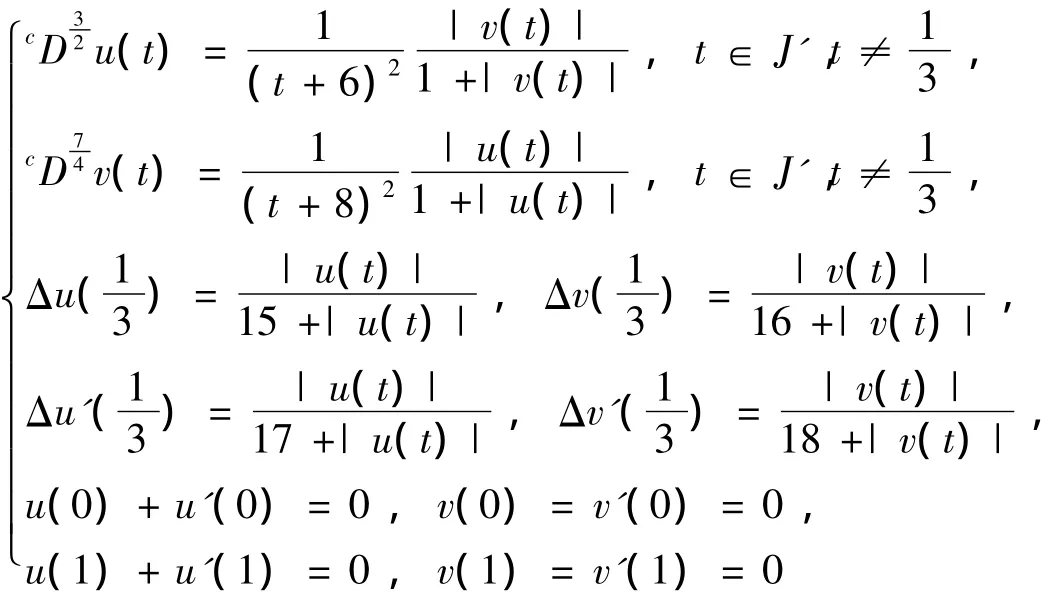
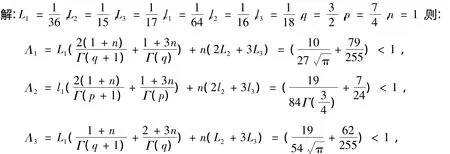
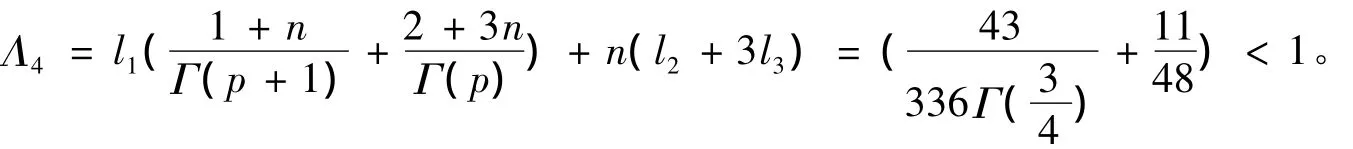
满足定理4的条件，此边值问题有唯一解。

/References:

［1］ AHMAD B，SIVASUNDARAM S.Existence results for nonlinear impulsive hybrid boundary value problems involving fractional differential equations［J］.Nonlinear Analysis:Hybrid Systems，2009，3:251-258.

［2］ ZHAO Aimin，BAIZhenguo.Existence of solutions to first-order impulsive periodic boundary value problems［J］.Nonlinear Analysis，2009，71(5/6):1970-1977.

［3］ 郭少聪，郭彦平，陈悦荣.带p-Laplacian算子三点边值问题拟对称正解的存在性［J］.数学的实践与认识，2012，42(16):236-240.GUO Shaocong，GUOYanping，CHEN Yuerong.The existence of pseudo-symmetric positive solutions for three-pointboundary value problemswithp-Laplacian［J］.Mathematics in Practice and Theory，2012，42(16):236-240.

［4］ LIU Y J.A study on quasi-periodic boundary value problems for nonlinear higher order impulsive differential equations［J］.Appl Math Copmut，2006，183:842-857.

［5］ LIAN H R，PANG H H，GEWeigao.Triple positive solutions for boundary value problems on infinite intervals［J］.Nonlinear Anal，2007，67:2199-2207.

［6］ LIJiangli，NIETO JJ，SHEN Jianhua.Impulsive periodic boundary value problem of first-order diffferential equations［J］.JMath Anal Appl，2007，325:226-236.

［7］ YAO Linhong，ZHAO Aimin.Existence ofmultiple positive solutions for second or impulsive differential equations［J］.Joural of Shanxi University(Natural Science Edition)，2006，28(1):6-9.

［8］ 许晓婕，费祥历.三阶非线性奇异边值问题正解的存在唯一性［J］.系统科学与数学，2009，29(6):779-785.XU Xiaojie，FEIXiangli.Existence and uniquenessof positive solutions for third-order nonlinear singular boundary value problem［J］.JSys Sci＆Math Scis，2009，29(6):779-785.

［9］ 孙忠民，赵增勤.三阶微分方程组边值问题常号解的存在性［J］.系统科学与数学，2007，27(6):811-819.SUN Zhongmin，ZHAO Zengqin.The existence of constant-sing solutions of BVPs for third order differential systems［J］.JSys Sci＆ Math Scis，2007，21(6):811-819.

［10］ KAUFMAN E R，KOSMATOV N，RAFFOUL Y.A second-order boundary value problem with impulsive effects on an unbounded domain［J］.Nonlinear Analysis，2008，69:2924-2929.

［11］ YAOM P，ZHAO AM，YAN J.Peiodic boundary value problems of second-order impulsive differential equations［J］.Nonlinear Anal，2009，70(1):262-273.

［12］ LIAN H R，PANG H H，GEWeigao.Triple positive solutions for boundary value problems on infinite intervals［J］.Nonlinear Anal，2007，67(7):2199-2207.

［13］ BAID Y，XU Y T.Positive solutions and eigenvalue intervals of nonlocal boundary value problemswith delays［J］.JMath Anal Appl，2007，334:1152-1166.

［14］ SHIG L，MENG X R.Monotone iterative for forth-orderp-Lapacian boundary value problemswith impulsive effects［J］.App Math Comput，2006，181:1243-1248.

［15］ FRANCO D，NIETO J J，REGAN D O.Existence of solutions for first order ordinary differential equations with nonlinear boundary condition［J］.Appl Math Comput，2004，153:793-802.

［16］ PODLUBNY I.Fractional Differential Equations［M］.New York:Academic Press，1999.

［17］ MILLER K S，ROSSB.An Introduction to the Fractional Calculus and Fractional Differential Equations［M］.New York:Wiley，1993.

［18］ KILBASA A，SRIVASTAVA H M，TRUJILLO JJ.Theory and Applications of Fractional Differential Equations［M］.Holland:Elsevier B V，2006.

［19］ AGARWAL R P，DOSSANTOS JP，CUEVASC.Analytic resolventoperator and existence results for fractional integro-differential equations［J］.JAbstr Differ Equ Appl，2012，2(2):26-47.

［20］ 郭彦平，李春景，韩迎迎.带p-Laplace算子的三阶微分方程边值问题正解的存在性［J］.河北科技大学学报，2014，35(6):524-528.GUO Yanping，LIChunjing，HAN Yingying.Existence of positive solutions for boundary value problem of third-order differential equations ofwithp-Laplacian［J］.Journal of Hebei University of Science and Technology，2014，35(6):524-528.

［21］ 陈艳丽.二阶非线性积分-微分方程边值问题的正解［J］.河北师范大学学报(自然科学版)，2014，38(5):445-450.CHEN Yanli.Positive solutions of noulinear second-order boundary value problems for inteqgro-differential equations［J］.Journal of Hebei Normal University(Natural Science Edition)，2014，38(5):445-450.