基于保护协调配合的最小断点集选取方法
周晓霞
(三峡大学电气与新能源学院,湖北宜昌443002)
0 引 言
确定大规模复杂环网方向保护的最优配合顺序是现代电力系统继电保护整定计算领域的一个关键问题。不论是保护之间的定值配合,还是保护之间的动作时间配合,都需要确定一组整定起始点,即最小断点集[1,2]。作为复杂环网方向保护整定计算的起点,最小断点集的选择对系统保护整体协调配合性能具有重要影响[3]。因此,如何在多组可选最小断点集中,选择一组最佳保护整定配合起点,具有重要现实意义。文献[4]通过复杂网络理论评价节点重要度,将断点选在重要度较低节点的出口线路处,以有效地降低断点脆弱性对系统的影响。文献[5]通过线路电气介数的概念,进一步计算线路的重要度,将断点选在重要度较低节点的非重要出口线路处。
为了尽快地切除故障,减少设备及用户在大短路电流、低电压下运行的时间,降低设备的损坏程度,提高电力系统并列运行的稳定性,最小断点集的选择应有利于避免电网保护间的连续多级配合。据此,本文提出了基于保护协调配合的最小断点集选取方法。定义了电网各级保护间协调配合性能的评价指标,给出了该评价指标的计算方法,以及选取保护最佳整定配合起点的算法基本流程。
1 基本原理及实现方法
1.1 图的基本概念[6]
(1)有向图
有向图是抽象的有向边和顶点的集合,可以用一个二元组G=(V,E)来描述。其中,G表示一个有向图,V={v1,v2,…,vn}表示有向图G中顶点的集合,L={e1,e2,…,em}表示有向图G中有向边的集合。
(2)邻接矩阵
用邻接矩阵A=(aij)n×n表示和存储有向图G。其中,对于任意顶点vi,vj∈V,若存在一条由顶点vi指向顶点vj的有向边,则aij取值为1,反之,aij取值为0。
(3)基本路径
在有向图G=(V,E)中,有一组首尾相接的有向边组成的序列{e1,e2,…,em},如果ek(k=1,2,…,p)是由顶点vk-1指向顶点vk的有向边,则称该序列为从起点v0到终点vp的一条路径。顶点不重复的路径称为基本路径。
一条基本路径所含有向边的数目,称为这条基本路径的长度。在顶点vi到顶点vj的基本路径中,长度最长的基本路径称为最长基本路径。
1.2 评价指标
设电网有w个同级间相互配合的保护,有多组可选的最小断点集,Bk={d1,d2,…,dm}表示其中的第k
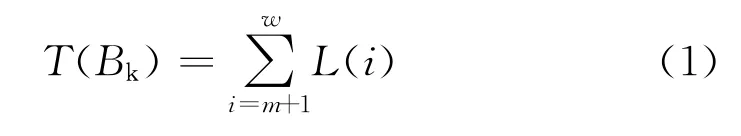
其中,
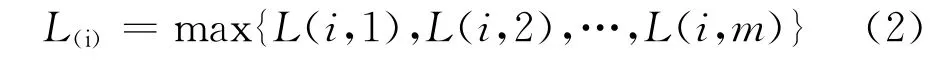
式中,L(i)表示第i个非最小断点处保护的整定配合级数;L(i,j)表示仅与第j个最小断点处保护配合时,第i个非最小断点处保护的整定配合级数,若第i个非最小断点处保护与第j个最小断点处保护无配合关系,则L(i,j)值为0,i=m+1,m+2,…,w,j=1,2,…,m,电网非最小断点处保护的数量为w-m。
通过考察电网方向保护配合级数总和,T(Bk)能够有效评价电网各级保护间的协调配合性能。T(Bk)值越小,表明该最小断点集越有利于避免电网保护间的连续多级配合。
1.3 算法的基本流程
选择保护最佳整定配合起点的基本流程如下。
(1)步骤一:以电网保护为顶点,以相邻线路保护间的整定配合关系为有向边,将电网保护及其整定配合关系抽象为一个有向图[7]。该有向图的邻接矩阵为A(aij)n×n,若保护i是相邻线路保护j的后备保护,则aij取值为1,否则取值为0,n为电网保护数量。
(2)步骤二:设电网有q组可选的最小断点集,分别记为B1,B2,…,Bq。则分别以上述各组最小断点集为电网保护的整定配合起点,按式(1)和式(2)计算其对应的评价指标T(B1),T(B2),…,T(Bq)。
以最小断点集Bk={d1,d2,…,dm}为例,其相应的T(Bk)计算如下。设邻接矩阵为A(aij)n×n中,最小断点d1,d2,…,dm处保护对应的顶点为v1,v2,…,vm,非最小断点处保护对应的顶点为vm+1,vm+2,…,vw。
a.在邻接矩阵为A(aij)n×n中,将顶v1,v2,…,vm对应行的非0元素全部置0,即得到以最小断点集Bk为电网保护整定配合起点时,描述电网保护间整定配合关系的邻接矩阵A′。
b.计算L(i,j),i=m+1,i=m+2,…,w,j=1,2,…,m。
在邻接矩阵A′对应的有向图中,采用深度优先搜索方法[8],搜索由顶点vi到顶点vj的最长基本路径,将该最长基本路径的长度赋值给L(i,j)。
c.按式(2)计算L(i),i=m+1,m+2,…,w。d.按式(1)计算T(Bk),k=1,2,…,q。
(3)步骤三:若最小断点集Bk(k=1,2,…,q)满足下列条件,则将其选择为电网保护的最佳整定配合起点。
T(Bk)=min{T(B1),T(B2),…,T(Bq)} (3)组最小断点集,dj表示该最小断点集Bk中的第j个断点,j=1,2,…,m。则以该Bk为电网保护的整定配合起点时,电网各级保护间协调配合性能的评价指标T(Bk)定义如下:
2 算例分析
系统接线及保护分布如图1所示。该环网共有14个同级间相互配合的保护(如:Ⅲ段保护),保护序号分别用阿拉伯数字1,2,…,14表示。
描述电网保护及其整定配合关系有向图的邻接矩阵A如下。

以文献[9]给出的6组可选最小断点集为例,验证本文方法的有效性。该6组可选最小断点集分别为:
B1={1,4,9,12},B2={2,5,8,11},B3={1,3,9,12},B4={1,7,9,12},B5={2,5,8,10},B6={2,5,8,14}
以B5={2,5,8,10}为电网保护的整定配合起点为例,描述电网保护间整定配合关系的邻接矩阵A′如下。

最小断点集B5为电网保护的整定配合起点时,其相应的评价指标L(i)和T(B5),i=1,3,4,6,7,9,11,12,13,14,计算结果如下。
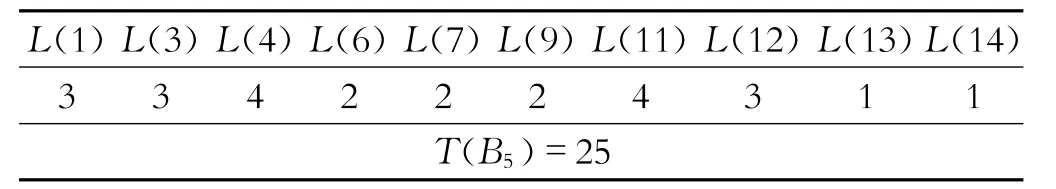
表1 评价指标L(i)计算结果
以上述6组最小断点集为电网保护的整定配合起点,分别计算其相应的评价指标T(Bk),k=1,2,3,4,5,6,结果如表2所示。
由表2可知,最小断点集B1满足式(3),将其选择为电网保护的最佳整定配合起点。与评价指标最高的最小断点集B2相比,最小断点集B1的评价指标降低了约22.7%,表明以最小断点集B1为电网保护整定配合起点,能有效避免电网保护间可能出现的连续多级配合,有利于快速切除电网短路故障和提高电力系统并列运行稳定性。

表2 评价指标T(B k)计算结果
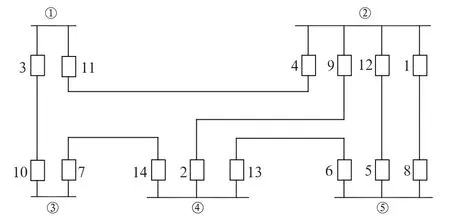
图1 系统接线及保护分布
3 结 论
本文提出了一种在多组可选最小断点集中实现保护整定配合起点选择的方法,给出了方法的基本原理和实现步骤。仿真结果表明,该方法能有效提高复杂环网中方向保护的整体协调配合性能。
[1]陈 绩,吕飞鹏,黄姝雅.确定复杂环网方向保护最小断点集的改进离散粒子群优化算法[J].电网技术,2008,32(12):90-94.
[2]Sharifian H,Abyaneh H A,Salman S K,et al.Determination of the Minimum Break Point Set Using Expert System and Genetic Algorithm[J].IEEE Transactions on Power Delivery,2010,25(3):1284-1295.
[3]Gajbhiye R K,De A,Soman S A.Computation of Optimal Break Point Set of Relays-An Integer Linear Programming Approach[J].IEEE Transactions on Power Delivery,2007,22(4):2087-2098.
[4]李运坤,吕飞鹏,陈 新,等.基于节点重要度估计得多组同基最小断点集选取方法[J].电力系统自动化,2010,34(12):58-60.
[5]张向亮,吕飞鹏,李运坤.基于保护重要度的多组同基最小断点集选取方法[J].电力系统自动化,2012,36(10):90-93.
[6]肖位枢.图论及其算法[M].北京:航空工业出版社,1992.
[7]刘 丹,吕飞鹏.基于网络化简和配合关系的最小断点集计算方法[J].电力系统自动化,2008,32(16):24-27.
[8]朱福喜,杜友福,夏定纯.人工智能引论[M].武汉:武汉大学出版社,2006.
[9]周文越,吕飞鹏,廖小君.基于人工蜂群算法的环网方向保护配合最小断点集计算[J].电力系统保护与控制,2013,41(6):77-81.

