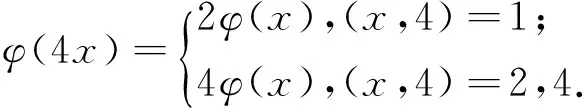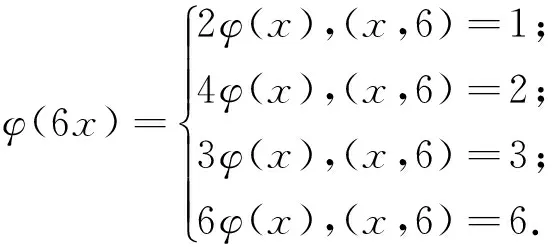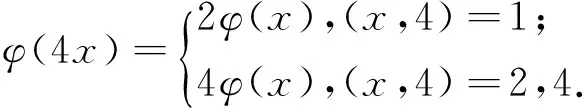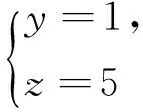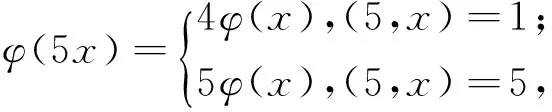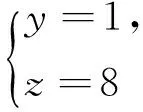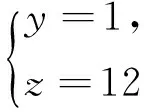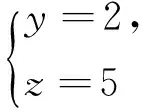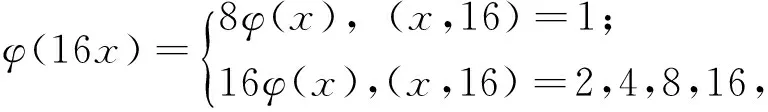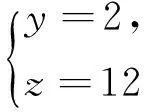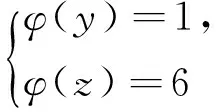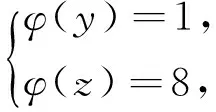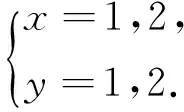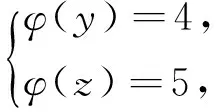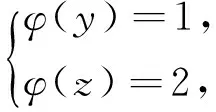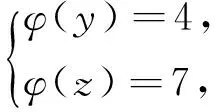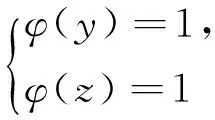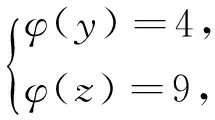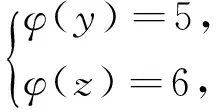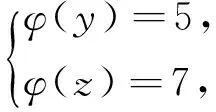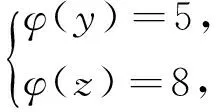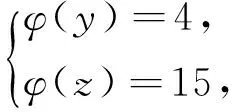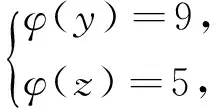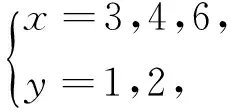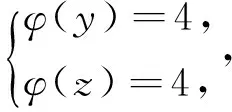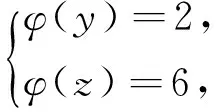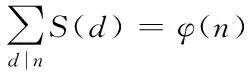一个包含Euler函数方程的正整数解
张四保, 杜先存
(1.喀什大学 数学与统计学院, 新疆 喀什 844006; 2.红河学院 教师教育学院, 云南 蒙自 661199)
一个包含Euler函数方程的正整数解
张四保1*, 杜先存2
(1.喀什大学 数学与统计学院, 新疆 喀什 844006; 2.红河学院 教师教育学院, 云南 蒙自 661199)
主要利用初等方法研究了方程φ(xyz)=3(φ(x)+φ(y)+φ(z))的可解性问题,给出了该方程的所有的正整数解,其中φ(n)为Euler函数.
Euler函数; 不定方程; 整数解

定理1方程
φ(xyz)=3(φ(x)+φ(y)+φ(z))
(1)
有正整数解:
(x,y,z)=(14,2,2),(18,2,2),(5,3,3),(8,3,3),(10,3,3),(3,3,3),(6,3,3),(13,3,4),(13,4,3),(5,3,6),(5,6,3),(3,3,6),(3,6,3),(2,2,14),(2,14,2),(2,2,18),(2,18,2),(3,3,5),(3,3,8),(3,3,10),(3,4,13),(3,6,5),(4,3,13),(6,3,5),(3,5,3),(3,8,3),(3,10,3),(3,13,4),(3,5,6),(4,13,3),(6,5,3).
1 主要引理

引理2[13]设n是整数,且n≥2,则φ(n) 引理3[12]对任意正整数n,p为素数,则 由于φ(xyz)=3(φ(x)+φ(y)+φ(z)),则有 φ(x)φ(y)φ(z)≤ 3(φ(x)+φ(y)+φ(z)). 从而有φ(x)φ(y)φ(z)≤3(φ(x)+φ(y)+φ(z)),即 φ(x)φ(y)φ(z)-3φ(x)= (φ(y)φ(z)-3)φ(x)≤3(φ(y)+φ(z)). (2) 下面将φ(y)φ(z)的值分以下两种情况分别加以讨论. 2.1 φ(y)φ(z)≤3 此时,φ(y)φ(z)≤2,则y,z有如下一些可能取值: (y,z)=(1,1),(1,2),(1,3),(1,4),(1,6),(2,1),(2,2),(2,3),(2,4),(2,6),(3,1),(3,2),(4,1),(4,2),(6,1),(6,2). 显然,当(y,z)=(1,1),(1,2),(2,1),(1,3),(3,1)时,方程(1)无正整数解. 当(y,z)=(1,4),(4,1)时,有φ(4x)=3(φ(x)+3)=3φ(x)+9.由于 由此可知,此时方程(1)无正整数解. 当(y,z)=(1,6),(6,1)时,有φ(6x)=3(φ(x)+3)=3φ(x)+9.由于 由此可知,此时方程(1)无正整数解. 当(y,z)=(2,2)时,有φ(4x)=3(φ(x)+2)=3φ(x)+6.由于 此时,当4φ(x)=3φ(x)+6,从而φ(x)=6,则x=14,18. 因而,方程(1)有正整数解(14,2,2,),(18,2,2,). 当(y,z)=(2,3),(3,2)时,有φ(6x)=3(φ(x)+3)=3φ(x)+9.根据以上φ(6x)的讨论可知,此时方程(1)无正整数解. 当(y,z)=(2,4),(4,2)时,有φ(8x)=3φ(x)+9.由于 因而,此时方程(1)无正整数解. 当(y,z)=(2,6),(6,2)时,有φ(12x)=3φ(x)+9.由于 因而,此时方程(1)无正整数解. 2.2 φ(y)φ(z)>3 此时,有φ(y)φ(z)≥4. 1)φ(y)φ(z)=4 此时,有 这8种情况. 因而,此时方程(1)无正整数解. 因而,此时方程(1)无正整数解. 因而,此时方程(1)无正整数解. 因而,此时方程(1)无正整数解. 因而,此时方程(1)无正整数解. 因而,此时方程(1)无正整数解. 2)φ(y)φ(z)=6 此时,有 3)φ(y)φ(z)=8 此时,有 4)φ(y)φ(z)=10 此时,有 仿φ(y)φ(z)=4情况的讨论可得,此时方程(1)无正整数解. 5)φ(y)φ(z)>10 由于φ(y),φ(z)均为正整数,所以有(φ(y)-1)(φ(z)-1)≥0,即φ(y)φ(z)+1≥φ(y)+φ(z). 由(2)有 所以,φ(x)=1,2,4. (I)φ(x)=1 此时,有φ(y)φ(z)=φ(x)φ(y)φ(z)≤φ(xyz)=3(1+φ(y)+φ(z)),于是有 (φ(y)-3)(φ(z)-3)≤12. 当(φ(y)-3)(φ(z)-3)≥0时,此时有(φ(y)-3)(φ(z)-3)=0,1,2,3,4,5,6,7,8,9,10,11,12. 当(φ(y)-3)(φ(z)-3)=0时,则φ(y),φ(z)至少有一个等于3,此时方程(1)无正整数解. 当(φ(y)-3)(φ(z)-3)=1时,有 此时3(1+φ(y)+φ(z))均为奇数,因而方程(1)无正整数解. 当(φ(y)-3)(φ(z)-3)=2时,有 此时方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=3时,有 此时3(1+φ(y)+φ(z))亦均为奇数,因而方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=4时,有 当(φ(y)-3)(φ(z)-3)=5时,有 此时3(1+φ(y)+φ(z))亦均为奇数,因而方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=6时,有 此时φ(y),φ(z)中有一个不成立,因而方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=7时,有 此时3(1+φ(y)+φ(z))为奇数,因而方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=8时,有 此时φ(y),φ(z)中至少有一个不成立,因而方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=9时,有 此时3(1+φ(y)+φ(z))为奇数,因而方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=10时,有 此时φ(y),φ(z)中至少有一个不成立,因而方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=11时,有 由于φ(x)=14无解[14],故而此时方程(1)无正整数解; 当(φ(y)-3)(φ(z)-3)=12时,有 此时φ(y),φ(z)中至少有一个不成立,因而方程(1)无正整数解. (II)φ(x)=2 此时,有 2φ(y)φ(z)=φ(x)φ(y)φ(z)≤ φ(xyz)=3(2+φ(y)+φ(z))< 4(2+φ(y)+φ(z)), 于是有(φ(y)-2)(φ(z)-2)<8. 当(φ(y)-2)(φ(z)-2)=0时,则φ(y),φ(z)中至少有一个等于2.当φ(y)=2时,方程(1)有正整数解(3,3,5),(3,3,8),(3,3,10),(3,3,3),(3,3,6),(3,4,13),(3,6,5),(3,6,3),(4,3,13),(6,3,3),(6,3,5). 从而,此时方程(1)有正整数解(3,3,5),(3,3,8),(3,3,10),(3,3,3),(3,3,6),(3,4,13),(3,6,5),(3,6,3),(4,3,13),(6,3,3),(6,3,5),(3,5,3),(3,8,3),(3,10,3),(3,6,3),(3,13,4),(3,5,6),(4,13,3),(6,5,3). 当(φ(y)-2)(φ(z)-2)=1时,有 此时(1)无正整数解; 当(φ(y)-2)(φ(z)-2)=2,3,5,6,7时,φ(y),φ(z)中至少有一个不成立; 当(φ(y)-2)(φ(z)-2)=4时,有 此时方程(1)无正整数解. (III)φ(x)=4 此时,方程(1)可化为: 4φ(y)φ(z)=φ(x)φ(y)φ(z)≤ φ(xyz)=4(4+φ(y)+φ(z)), 于是有0≤(φ(y)-1)(φ(z)-1)≤5. 当(φ(y)-1)(φ(z)-1)=0时,有φ(y)=1或φ(z)=1,此时方程(1)无正整数解. 当(φ(y)-1)(φ(z)-1)=1时,有φ(y)=2,φ(z)=2,此时方程(1)有正整数解(5,3,3),(5,3,6),(5,6,3),(8,3,3),(10,3,3). 当(φ(y)-1)(φ(z)-1)=2,4时,φ(y),φ(z)中至少有一个不成立,因而此时方程(1)无正整数解; 当(φ(y)-1)(φ(z)-1)=3时,有 此时方程(1)无正整数解; 当(φ(y)-1)(φ(z)-1)=5时,有 此时方程(1)无正整数解. 对上述正整数解进行归纳可得本文结论.证毕. [1] 吕志宏. 两个数论函数及其方程[J]. 纯粹数学与应用数学, 2006, 22(3):303-306. [2]SierpinskiW.Surunproprietedelafunctionφ(n)[J]. Publ Math Debrecen, 1956, 4: 184-185. [3] Schinzel A. Sur l'equationφ(x+k)=φ(x)[J]. Acta Arith, 1958, 4: 181-184. [4] Schinzel A, Wakulicz A. Sur l'equationφ(x+k)=φ(x) (II) [J]. Acta Arith, 1959, 5: 425-426. [5] Ballew R. Table ofφ(x+k)=φ(x) [J]. Math Comput, 1976, 30: 189-190. [6] Schinzel A. Sur l’equationφ(x)=m[J]. Elem Math, 1956, 11: 75-78. [7] Kevin Ford. The number of solutions ofφ(x)=m[J]. Annals of Mathematics, 1999, 150: 1-29. [8] 陈国慧. 一个包含Euler 函数的方程[J]. 纯粹数学与应用数学, 2007, 23(4):439-445. [9] 杨仕椿. 关于Euler 函数的两个问题[J]. 天津师范大学学报:自然科学版, 2004, 24(2):42-44. [10] 陈 斌. 一类包含Smarandache函数和Euler函数的方程[J]. 西南大学学报:自然科学版, 2012, 34(2):70-73. [12] 孙翠芳,程 智. 关于方程φ(xyz)=2(φ(x)+φ(y)+φ(z)) [J]. 数学的实践与认识, 2012, 42(23):267-271. [13] Rosen K H. Elementary theory and its applications[M]. Fifth edition. New Jersey: Pearson Educatin Inc Addison Wesley, 2005. [14] 姜友谊. 关于Euler 函数方程φ(x)=m的解[J]. 重庆工业管理学院学报, 1998, 12(5):91-94. The positive integer solutions of an equation involving the Euler function ZHANG Sibao1, DU Xiancun2 (1.School of Mathematics and Statistics, Kashgar University, Kashgar, Xinjiang 844006;2.College of Teacher Education, Honghe University, Mengzi, Yunnan 661199) The solvability of the equationφ(xyz)=3(φ(x)+φ(y)+φ(z))isstudiedbyelementarymethodsinthispaper,andallpositiveintegersolutionsoftheequationareobtained,whereφ(n)istheEulerfunction. Euler function; Diophantine equation; integer solutions 2014-12-26. 江苏省教育科学“十二五”规划课题项目(D201301083);新疆维吾尔自治区高校科研计划重点项目(XJEDU2008I31);喀什大学校内课题项目(112390). 1000-1190(2015)04-0497-05 O156< class="emphasis_bold">文献标识码: A A *E-mail: sibao98@sina.com.
2 定理的证明