点与积分变换在微分方程求解中的应用①

朱春蓉，吴吟黎

(安徽师范大学数学计算机科学学院，安徽芜湖241000)

0 引 言

变换是求解或化简微分方程的重要方法之一.在本科学习阶段，《常微分方程》和《数学物理方程》是学生为以后从事微分方程研究学习的最基础的两门课程.立足于这两门课程，并结合一些较新的微分方程研究成果，讨论了微分方程教学中常常出现的变换.在文献［1 ～6］中，介绍了各种求解常微分方程的方法.在不同类型的微分方程中，求解方法也不同，也使用了不同的变换.在文献［7 ～8］中，讨论了变量变换在常微分方程中的应用.一些微分方程中的变换分为两大类:一类是点变换;另一类是积分变换.在点变换中，又可将变换分为自变量变换和因变量变换两种情形.将从求解或简化一些常微分方程和偏微分方程的角度分别讨论这几类变换的应用.希望通过对这些变换的讨论，让学生进一步掌握在微分方程学习中变换的技巧，并为以后微分方程的学习和研究打下基础.

1 点变换

在各种微分方程中，点变换较为常见，可以分为自变量变换和因变量变换两种类型.下文将分别讨论这两种变量变换.

2.1 自变量变换

自变量变换常常应用于求解或化简变系数的微分方程.在线性常微分方程中，通过自变量变换把变系数的线性微分方程转化为常系数的线性微分方程，从而得到求解［1］.在偏微分方程中，自变量变换可以减少变系数的个数，从而令方程得到简化［9］.

为了求解Euler 方程

作自变量变换x=et，即t=lnx，则它转换为n 阶常系数齐次线性微分方程

其中ai，bi(i=1，…，n)都是常数.这里考虑的是x＞0 的情形，当x ＜0 时，使用变量变换x=-et.通过求解方程(2)，再变量代回t=ln|x|从而得到方程(1)的通解.下面将给出一个例子来演示这个过程.

例1 求解方程

解 通过变量变换x=et，则t=lnx，代入方程(3)，方程(3)转化为

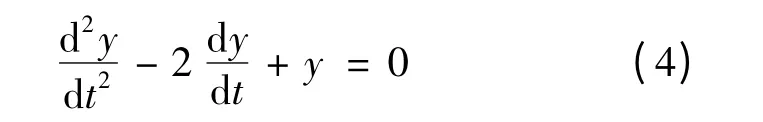
求解方程(4)，得到

因此，方程(3)的通解为

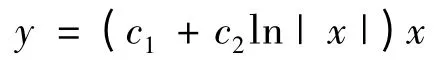
其中ci是任意常数.

在变系数非线性反应扩散方程

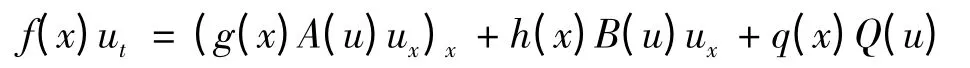
中，利用自变量代换

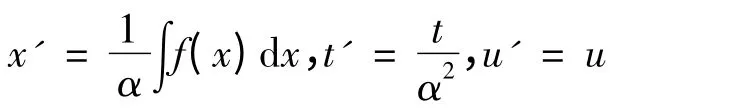
得到

其中g′(x)=f(x)g(x)，h′(x′)=αh(x)，q′(x′)Q′(u′)

显然，这里只进行了自变量变换，且方程得到了简化.对变换后的方程可以利用广义条件对称方法构造其精确解，再通过逆变换就可以得到原变系数非线性反应扩散方程的解［9］.

2.2 因变量变换

因变量变换在常微分方程的求解过程中应用较多，文献［7］详细地介绍了因变量变换在各种常微分方程求解中的应用情况.在本文中将对偏微分方程中的一些因变量变换进行讨论.

在偏微分方程中，为了构造弦振动方程非齐次边界条件初边值问题

的解，可以通过因变量变换

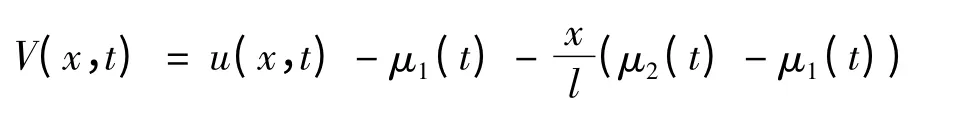
把该问题转换为齐次边界条件的初值问题

我们可以通过齐次化原理及分离变量法构造该问题的解［10］.类似地，这里采用的因变量变换还可用求解其它线性偏微分方程的非齐次初边值问题.

在热传导方程

中，采用变量代换v=lnu，该方程被转换为

由文献［11］知，利用不变子空间方法，方程(6)在多项式空间W2=L{1，x2}中可以构造解

再经过变量代换u=ev，我们就可以得到热方程的基本解

类似的变量变换在文献［11］中还大量被使用于求解一些非线性偏微分方程.

3 积分变换

在微分方程中常常使用两类积分变换，一类是Laplace 变换，另一类是Fourier 变换.事实上，在文献［12］中指出，这两类积分变换可以看成是相通的.Laplace 变换一般用于常系数线性常微分方程(组)初值问题的求解中，其主要思想是将常系数线性常微分方程初值问题转化为代数方程来求解;Fourier 变换一般用于线性偏微分方程初值问题的求解中，其主要思想是将线性偏微分方程初值问题转化为线性常微分方程初值问题来求解.在有些偏微分方程初边值问题中也会采用Laplace变换.

考虑微分方程初值问题

其中ai是常数，f(t)连续且满足原函数的条件.设

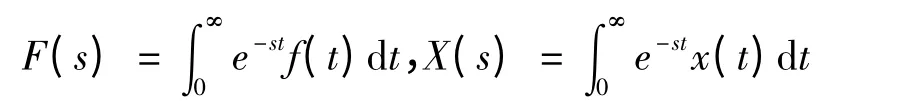
利用Laplace 变换的相关性质可以得到

其中

再由Laplace 变换表可以得到x(t)［1］.下面将给出一个例子解释这个过程.

例2 求解常微分方程初值问题

解 先令λ=t-1 问题化为

再对变换后的方程两边作Laplace 变换，得到

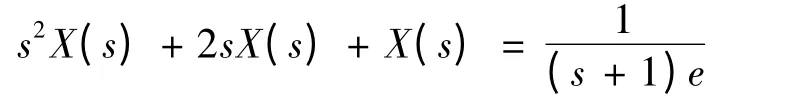
因此，

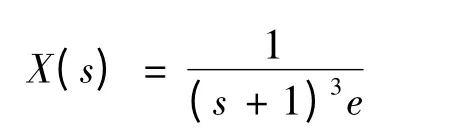
由Laplace 变换表得到

从而得到原问题的解

本文以热传导方程的柯西问题为例解释Fourier 变换求解线性偏微分方程初值问题的过程［10］.考虑热传导方程的柯西问题

设

对原问题进行Fourier 变换，则有

求解此常微分方程初值问题，得到

而

因此，可得到齐次热方程的柯西问题的解

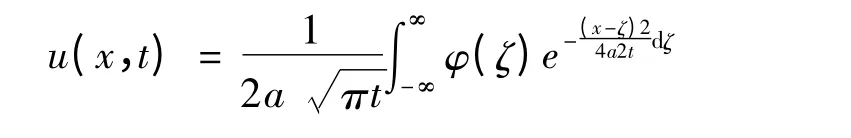
［1］ 王高雄，周之铭，朱思铭等.常微分方程(第三版)［M］北京:高等教育出版社，2006:20－283.

［2］ Braun M.Differential Equations and Their Applications［M］.Berlin:Springer－Verlag，1993:87－148.

［3］ 全生寅.论N 阶常微分方程的Laplace 变换法［J］.青海大学学报，2000，18(5):61－63.

［4］ 米荣波，沈有建.三阶欧拉方程求解的简化常数变易方法［J］.海南师范大学学报，2008，21(3):260－263.

［5］ 王彦海.一类高阶变系数线性微分方程的解法［J］.陕西师范大学学报，1999，24(3):53－55.

［6］ 龚东山，刘岳巍.特征函数在高阶常系数微分方程特解计算中的应用［J］.吉林师范大学学报，2008，30(4):8－10.

［7］ 张海，谢秀娟.变量代换法求解常微分方程［J］.安庆师范学院学报，2010，16:82－87.

［8］ 张东.变量代换法在求解微分方程问题中的应用［J］.辽宁交通高等专科学校学报，2003，5(4):54－55.

［9］ 万晖.带有源项的变系数非线性反应扩散方程的精确解［J］.物理学报，2013，62(9):090203.

［10］ 谷超豪，李大潜，陈恕行等.数学物理方程(第三版)［M］.北京:高等教育出版社，2012:35－89.

［11］ Galaktionov V A，Svirshchsevskii S R.Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics［M］.London:Chapman and Hall/CRC，2007:1－46.

［12］ 顾樵.数学物理方法［M］.北京:科学出版社，2012:17－23.