Existence of multiple positive solutions for(p,n-p)right focal boundary value problem with sign changing nonlinear term

BAI Mei,REN Lishun,HU Hongan

Higher order boundary value problems for ordinary differential equations arise naturally in technical applications[1-6].So far,higher order boundary value problems have not been documented as well as that for second order problems.In this paper,we study the existence of multiple positive solutions for(p,n-p)right focal boundary value problem(P)when the nonlinearity f is negative somewhere

We note that several existing results on the positive solutions have been established for higher order conjugate boundary value problems[1,2,6-9]and higher order right focal boundary value problems[10],respectively.In these papers,the condition that the nonlinearity f is nonnegative is a key factor.In the case of n=2,if the nonlinearity is nonnegative,then the solution u is concave down;if the nonlinearity f is negative somewhere,then the solution u is no longer concave down.However,in the case of n＞2,the solutions of problems(P)generally do not possess the concavity in any case.

In 1996,Anuradha,Hai and Shiviji[11]studied the existence of positive solutions for second order ordinary differential boundary value problem under the conditions(A1)and(A2)whenλ＞0 is small enough,where

(A1)there exists M＞0 such that f(t,u)≥-M for(t,u)∈[0,1]×[0,+∞);

(A2)holds uniformly on[α,β]⊂ (0,1),whereα,βwithα＜βare given constants.

Motivated by their work,the authors[12]of studied the existence of positive solutions for n order right focal boundary value problem.The purpose of this paper is to provide a sufficient condition for the existence of multiple positive solutions to problem(P).We shall apply the method arisen in our earlier studies[13-15].The main ingredient is the Krasnosel’skii fixed point theorem of cone expansion-compression type.

The main results of this paper are listed as follows:

Theorem 1 Assume that the conditions(A1),(A2)and f(t,0)for t∈[0,1]are satisfied,then the problem(P)has at least two positive solutions ifλ＞0is small enough.

The proof of above theorem is based on the following Guo-Krasnoselskii’s fixed point theorem[8,16].

Theorem 2 Let E be a Banach space,and let K⊂E be a cone.AssumeΩ1,Ω2are bounded open subsets of E with 0∈Ω1,Ω1⊂Ω2,and let A:K∩ (Ω2Ω1)→K be a completely continuous operator such that one of the following two conditions holds

(i)‖Au‖≤‖u‖,u∈K∩∂Ω1,and‖Au‖≥‖u‖,u∈K∩∂Ω2,

(ii)‖Au‖ ≥‖u‖,u∈K∩∂Ω1,and‖Au‖≤‖u‖,u∈K∩∂Ω2,then A has a fixed point in K∩(Ω¯2Ω1).

1 The Preliminary Lemmas

Lemma 1[8]Let G(t,s)be the Green’s function for

then

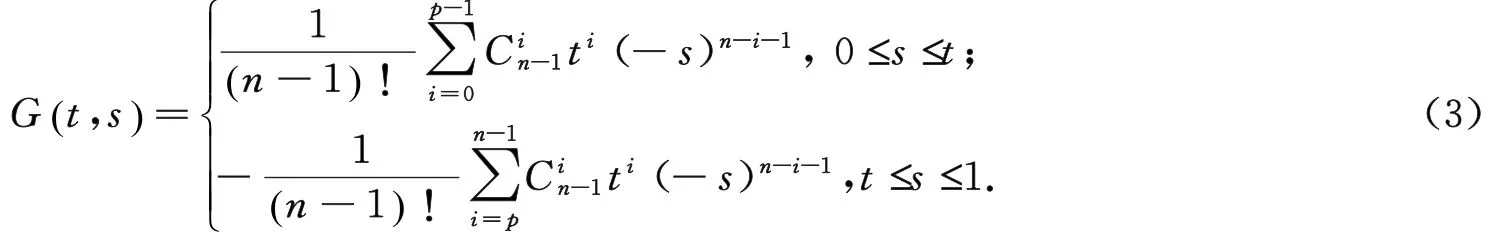
Lemma 2 The Green’s function G(t,s)has the following properties

(i)(-1)n-pG(i)t,s() ≥0,0≤i≤p-1 and-1()n-iG(i)t,s() ≥0,p≤i≤n-1,where

(ii)For(t,s)∈[0,1]×[0,1],we have(-1)n-pG t(,s)≤ (-1)n-pG( 1,s)

Proof (i)see[8];(ii)is an immediate consequence of(i).

Lemma 3[8]Suppose that u∈C(n-1)[0,1]∩C(n)(0,1)satisfies

Then

where q(t)=tp,‖u‖

Lemma 4[12]Let¯ωbe the unique solution of the right focal boundary value problem

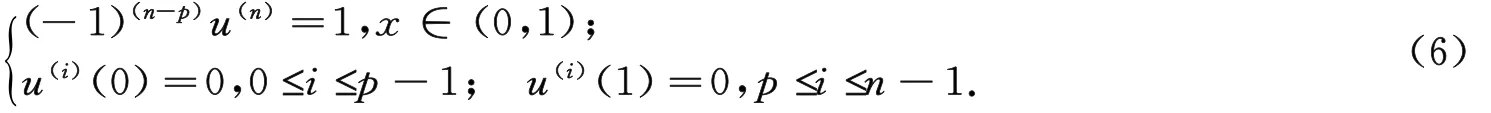
Then

where

2 Proof of the Theorems 1

Proof Letλ∈0,Λ(),z=λΜ¯ω,g t,u(),where

According to the Theorem 1 in[12],there exists a positive solution¯u(t)for the following boundary problem

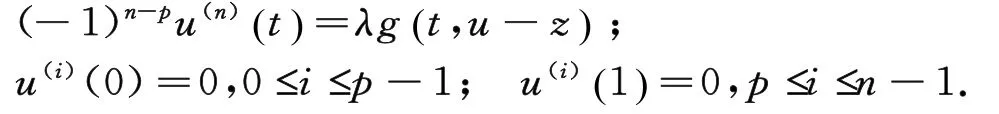
Moreover,the solution¯u(t)also satisfies

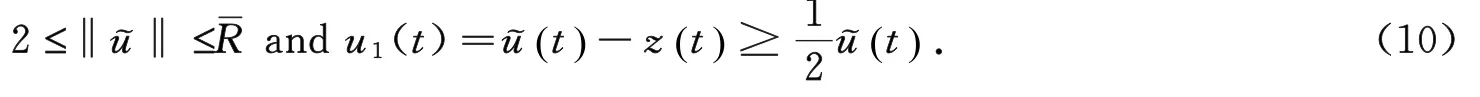
Thus,the(p,n-p)right focal boundary value problem(P)has a positive solution u1satisfying‖u1‖≥1.

Now,we prove that problem(P)has another positive solution u2satisfying‖u2‖＜1.In order to find the second positive solution of problem(P),we set

It is easy to see that if the condition f(t,0)＞0,t∈[0,1]holds,then there exist two constants a,b∈(0,∞),such that

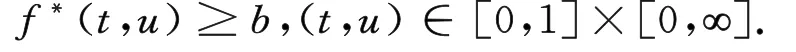
It is easy to see that f*(t,u)≥b for(t,u)∈ [0,1]×[0,∞).

Next,we consider the auxiliary equation

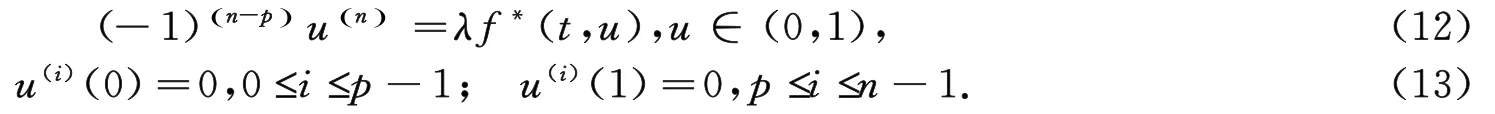
It is easy to check that(12)-(13)is equivalent to the fixed point equation

where

Using Lemma 3,it is easy to check that F:K→K is completely continuous and F K()⊂K.Let

where

Chooseλ∈ (0,Λ1)andΩ3={u∈C[0,1]|‖u‖ ≤H}.We have that

Therefore

From(A2)we know that

holds uniformly on[α,β]⊂ [0,1],α＜β.This means that there exists a constant r:r＜H,such that

where

Then for u∈K and‖u‖=r,we have

Thus,we may letΩ4={u∈C[0,1]|‖u‖＜r}such that‖Fu‖≥‖u‖,u∈K∩∂Ω4.It follows from the second part of Theorem 2 that(12)-(13)has a positive solution u2satisfying

We can conclude that u2is also a solution of problem(P).Thus,we know that problem(P)has two distinct positive solutions u1and u2forλ∈ (0,Λ1). ❙

[1]Agarwal R P,O'regan D.Multiplicity results for singular conjugate focal and(n,p)problems[J].Journal of Differential Equations,2001,170:142-156.

[2]Lan K Q.Multiple positive solutions of conjugate boundary value problems with singularities[J].Applied Mathematics and computation,2004,147:461-474.

[3]Eloe P W,Henderson J.Inequalities based on a generalization of concavity[J].Proc.Amer.Math.Soc.,1997,125(7):2103-2107.

[4]Fink A M,Gatica J A.Positive solutions of second order system of BVPs[J].J.Math.Anal.Appl.,1993,180:933-108.

[5]Ma R.Multiplicity results for a third order boundary value problem at resonance[J].Nonlinear Analysis TMA,1998,32(4):4933-499.

[6]Li Y J,Gao W J.Twin nonnegative solutions for(p,n-p)conjugate boundary value[J].J.of Mathematical Research and Exposition,2006,26(2):299-310.

[7]Eloe P W,Henderson J.Singular nonlinear(n-k,k)conjugate boundary value problems[J].J.Differential Equations,1997,133:136-151.

[8]Agarwal R P,O'regan D.Two solutions to singular boundary value problems[J].Proc.Amer.Math.Soc.,2000,128:2085-2094.

[9]Ma R,Wang H.On the existence of positive solutions of fourth order ordinary differential equations[J].Applicable A-nalysis,1995,59:225-231.

[10]Yao Q L.Positive solutions of nonlinear(p,n-p)focal boundary value problems[J].J.of University of Science and Technology of China,2009,39(3):241-246.

[11]Anuradha V,Hal D D,Shivaji R.Existence results for superlinear semipositive boundary value problems[J].Proc.A-mer.Math.Soc.,1996,124(3):757-763.

[12]Ren L S,Xing X Z.Positive solutions for semipositive(p,n-p)right focal boundary value problems[J].Henan sciences,2005,23(5):628-631.

[13]Ren L S,Wang Z G.Existence of multiple positive solutions on the three point boundary value problems[J].Chin.Quart.J.of Math.,2007,22(3):406-411.

[14]Ren L S,An Y K.Positive solutions for semipositive three point boundary value problems[J].J.of shaanxi Nor.Univer,2004,32(3):31-33.

[15]Ma R,Ren L S.Positive solutions for nonlinear m-Points boundary value problems of Dirichlet type via fixed point index theory[J].Applied Mathematics Lettles,2003,16(6):663-670.

[16]Wang H.On the existence of positive solutions for semilinear elliptic equations in annulus[J].J.Differential equations,1994,109:1-8.