带梯度项奇异抛物方程解的存在性及渐近行为*
夏 莉, 李敬娜, 王 玲, 张园园
(1.广东财经大学 数学与统计学院,广东 广州 510320;2.暨南大学 信息科学技术学院 数学系, 广东 广州 510632;3.广东水利电力职业技术学院 数学部, 广东 广州 510635;4.西南财经大学 证券与期货学院,四川 成都 611130)
带梯度项奇异抛物方程解的存在性及渐近行为*
夏 莉1, 李敬娜2, 王 玲3, 张园园4*
(1.广东财经大学 数学与统计学院,广东 广州 510320;2.暨南大学 信息科学技术学院 数学系, 广东 广州 510632;3.广东水利电力职业技术学院 数学部, 广东 广州 510635;4.西南财经大学 证券与期货学院,四川 成都 611130)
利用抛物正则化方法及上下解方法、Fatou引理等,研究了一类带梯度项奇异抛物方程非负古典解,得到了该解的存在性及相应的渐近行为.
梯度项;奇异性; 存在性; 渐近行为
考虑下面一类抛物方程:
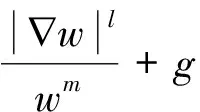
(1)
满足如下初边值条件:

(2)
w(x,0)=ψ(x),x∈Ω,
(3)
这里ΩT=Ω×(0,T],Ω⊂RN(N≥2)是一个具有光滑边界∂Ω的有界区域,T,λ,l,m均为正数.
问题 (1)~(3) 近年来得到了很多关注. 当l=2,m=1时, 该问题古典解及弱解的存在性、唯一性,解的渐近行为获得了证明,参见文献[1,2]. 当l=2, 1≤m<2时, 周文书及雷沛东[3]证明了问题(1)~(3)在一维空间中多个弱解的存在性. 当l=2,m>0时, 文献[4]研究了上述问题的弱解在t→∞时的渐近行为. 2014年,I.D.Bonis及D.Giachetti[5]还证明了l=2, 0 (H3)m>0,m+1≤l≤2或m 引理1[2]在假设条件(H1)(H2)下, 下面的初边值问题 wt-Δw=g(x,t), (x,t)∈ΩT, (4) w(x,0)=ψ(x),x∈Ω, 本文主要结果如下: (5) 这里C0,β是两个确定的正数,w0是引理1中初边值问题的唯一古典解. 而且, 当λ→∞时, (6) 特别当2m≤l≤2时, 令λ→0, 则 (7) 下面我们证明定理1. 由于方程(1)在w(x,t)=0具有奇异性, 先将其正则化为: (8) 将上述不等式中不等号反向, 可得古典下解的定义. (9) 这里β≥1均是待定的正数, 且β的选取与l,m的取值有关. 证明 由比较原理(可参考文献[6]中Theorem9.1)知, 只需证明 (10) 上面第一个不等式由(4)及λ>0易证. 下面证明第二个不等式. 选取β≥1, 简单计算及适当放缩后可得 则(10)式成立. 现在给出wε的一致有界性估计. 这里M不依赖于ε. 证明 由引理2及与文献[2]中Lemma2.3类似的方法易证得上述结论. 最后证明(5)~(7). 首先证明如下几个引理. 引理4 下式成立: 这里C不依赖于λ. 证明 对方程(8)两边同乘以wεk(k≥0), 并在ΩT上积分可得: (11) (12) 这里C不依赖于λ. 在(12)中取k=m即得引理4的结论. 引理5 当2m≤l≤2时, 下式成立: 这里C不依赖于λ. 证明 由(4)式及(8)式可得: 最后, 由(9)及上述两个引理易得(5)~(7), 定理1证毕. [1] XIA L, LIU Q, YAO Z A.Existence of the maximal weak solution for a class of singular parabolic equations [J]. J Math Anal Appl, 2012, 387: 439-446. [2] XIA L, YAO Z A.Existence, uniqueness and asymptotic behavior of solutions for a singular parabolic equation[J]. J Math Anal Appl, 2009, 358: 182-188. [3] ZHOUW S, LEI P D. A one-dimensional nonlinear heat equation with a singular term[J]. J Math Anal Appl, 2010, 368: 711-726. [4] MARTíNEZ-APARICIO P J, PETITTA F. Parabolic equations with nonlinear singularities[J]. Nonlinear Analysis, 2011, 74: 114-131. [5] BONIS I D , GIACHTTI D.Singular parabolic problems with possibly changing sign data[J]. Discrete and Continuous Dynamical Systems, Series B, 2014, 19: 2 047-2 064. [6] LAADYZENSKAJA O A, URALCEVA N N. Linear and quasilinear elliptic equations[M].New York: Academic Press, 1968:449-475. [7] LIEBERMAN G M. Second order parabolic differential equations[M].Beijing: World Scientific Publishing Co Pte Ltd, 2003:200-213. 责任编辑:龙顺潮 Existence and Asymptotic Behavior of Solutions for Some Singular Parabolic Equation with Gradient Term XIALi1,LIJing-na2,WANGLing3,ZHANGYuan-yuan4* (1.College of Mathematics and Statistics, Guangdong University of Finance and Economics, Guangzhou 510320;2. Department of Mathematics,College of Information Science and Technology Jinan University, Guangzhou 510632;3. Department of Mathematics, Guangdong Technical College of Water Resources and Electric Engineering, Guangzhou 510635;4. School of Securltiesand Futures,South Western University of Finance and Economics,Chengdu 611130 China) Using parabolic regularization method, sub-super solution method and Fatou Lemma etc., we discuss nonnegative classical solutions of some singular parabolic equation with gradient term, existence and asymptotic behavior of the solutions are obtained. gradient term; singularity; existence; asymptotic behavior 2014-11-21 国家自然科学基金项目(11201311, 11201181);四川省教育厅一般项目(15ZB0473) 张园园(1986— ),女,重庆人,博士,副教授.E-mail:yyzhang@swufe.edu.cn O 175 A 1000-5900(2015)02-0016-04