Duffing振子和Van der Pol振子耦合的动力学行为分析
王晓东, 杨绍普, 赵志宏
(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.河北省交通安全与控制重点实验室,河北 石家庄 050043)
Duffing振子和Van der Pol振子耦合的动力学行为分析
王晓东1,2, 杨绍普1,2, 赵志宏2
(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.河北省交通安全与控制重点实验室,河北 石家庄 050043)
针对耦合非线性混沌振子复杂的动力学行为,本文将Duffing振子和Van der Pol振子进行耦合,建立了Duffing振子和Van der Pol振子的耦合模型。与单个振子相比,耦合Duffing振子和Van der Pol振子表现出了更加丰富的动力学特性,采用Simulink仿真的方法,通过不同策动力幅值、不同耦合系数、不同频率下耦合非线性振子的相图和庞加莱截面图分析了耦合非线性振子的动力学行为,研究了耦合振子对微弱周期信号的敏感性和对噪声的免疫力,并将此模型应用于微弱信号检测的研究中。
混沌;耦合振子;微弱信号检测;仿真
0 引言
近年来, 对混沌的研究从低维时间系统转向高维时空系统。将若干不同的非线性振子(如Van der Pol振子、Duffing振子等)相互耦合, 构成的耦合非线性振子系统, 是研究时空混沌的较为理想的模型[1-2]。由于耦合系统兼有两个振子的共同特性,会表现出更加复杂的动力学行为,所以耦合振子的动力学行为在理论和应用中具有重要意义, 因而日益受到重视。经典的Duffing 及Van der Pol振子虽然在表达形式上很简单,但是由于具有丰富的动力学特性而极具代表性,它们常常被用来模拟系统的非线性特性,比如用耦合非线性振子系统描述和处理生物学、化学、光学、凝聚态物理学等众多领域的物理过程。各国学者对耦合振子系统的研究大致包括两方面工作,即系统的动力学行为和系统的控制与同步[3]。长期的实验发现,耦合振子和单个振子相比具有更加复杂的动力学行为。
本文研究了Duffing振子和Van der Pol振子相互耦合的动力学行为,对于这方面的文献相对还比较少,文献[4]依照它们各自的非线性特点耦合到一起,发现了一些特性,依然具有Duffing振子的特性,即对于微小扰动的极其敏感性和对噪声的免疫力[5-8]。鉴于此特性,对此系统做了实验分析和动力学分析,而且上述两大特性可以较为灵敏的将微弱信号从噪声中提取出来,在抑制噪声的同时,信号未被削弱,能有效降低噪声干扰,进行高灵敏度测量[9-11]。在混沌学中,一个非线性系统,其参数的变化有时会引起系统发生本质变化。这种变化反映到系统相图中是由混沌态变为周期态。本文通过数值仿真的方法,研究了此耦合非线性系统的这种本质的变化,并将其应用于微弱信号检测中,取得了一定的效果。
1 模型的建立
Duffing振子和Van der Pol振子组成非线性的耦合系统如下
(1)
式中,c表示Duffing振子的阻尼系数;k表示耦合系数;k的取值越大说明耦合的强度越高,不同振子间的同步性越强,当k=0时,两个系统的耦合作用完全消失;ω表示角频率;fcos(ωt)表示周期的驱动力;μ表示VanderPol振子的阻尼系数;f为周期策动力的幅值,当其他参数固定的时候,系统随着fcos(ωt)的幅值变化而有规律的变化。
由数学模型,可建立Duffing振子和Van der Pol振子耦合系统的仿真模型,如图1所示。为了说明耦合系统的工作原理取fcos (ωt)为周期策动力,及系统频率ω=1.0 rad/s,k=0.8,c=0.5,μ=0.8,随着周期策动力振幅f由0值逐渐增大,系统状态出现有规律的变化:经历同宿轨迹,分岔轨迹,混沌轨迹和大尺度周期状态。

图1 Duffing振子和Van der Pol振子耦合系统的仿真模型
Duffing和Van der Pol耦合振子表现出丰富的非线性动力学特性,当策动力幅值f比较小时,它表现为围绕某一焦点做周期的运动(系统相图如图2(a)所示),随着策动力幅值f的逐渐增大,当超过某一阈值时,系统处于混沌状态(系统相图如图2(b)所示),相轨迹局限在某一个范围之内,继续增大激励信号的幅值f,当再次超过某个阈值之后,系统进入到周期状态(系统相图如图2(c)所示),相轨迹不再杂乱无章,而是沿着固定的轨道重复下去。
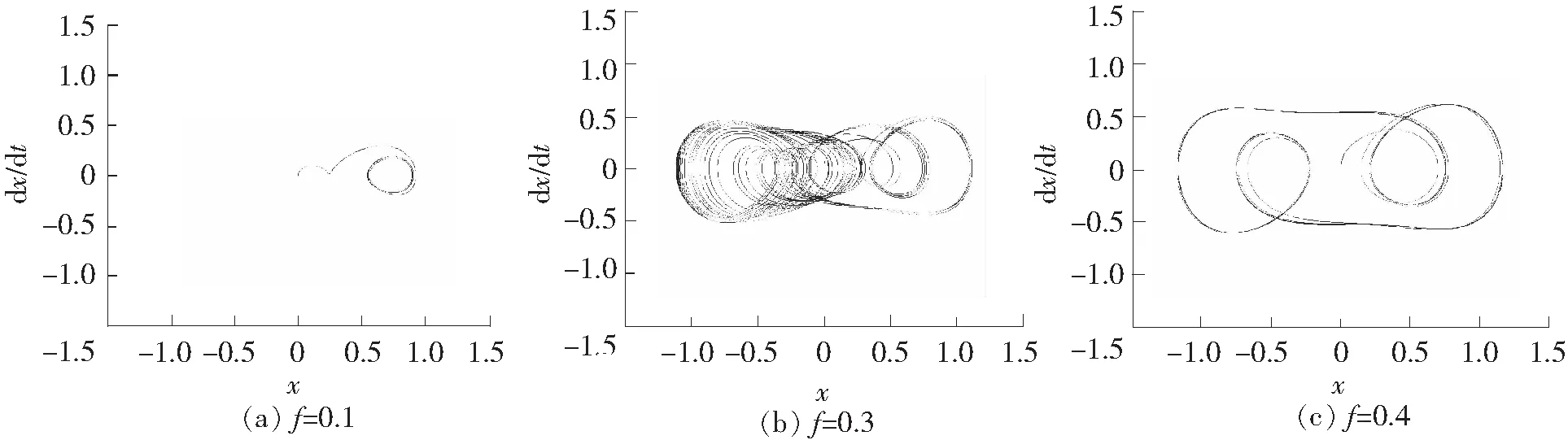
图2 不同激励幅值的系统相图
2 数值仿真实验
该实验用Matlab中的simulink模块进行仿真,对于耦合振子系统的状态方程
(2)
经过大量实验分析,耦合非线性系统动力学行为如图3所示,发现该系统对微弱的信号很敏感,选择其他的参数固定不变,当策动力幅值f1=0.342时,系统相图表现为混沌状态,系统的庞加莱截面图为混乱的点集如图3(c)所示,当策动力幅值f2=0.343时,系统相图表现为周期状态,系统的庞加莱截面图为只有3个点(周期3的运动)如图3(f)所示,由仿真实验看出此系统对于微小的扰动是很敏感的。

图3 不同激励幅值下Duffing振子和Van der Pol振子耦合系统的动力学行为
3 各个参数对耦合系统的影响
3.1 耦合系数对耦合系统的影响
对于上述Duffing振子和Van der pol振子耦合系统方程式(1),其中k代表耦合系数,其余各参数取值分别为μ=0.8,c=0.5,f=0.343,ω=1.0 rad/s,当k=0时,系统的耦合作用消失,随着k的逐渐增大耦合作用越来越强,但是对于系统的状态变化有了一定的影响,下面分别取k=0.1,0.5,1.0,1.5时,其它参数不变,对比下面一组系统的相图(如图4不同耦合系数取值下系统的动力学行为),可以发现耦合系数在一定的范围内对于系统的影响不是很大,但是超过某个范围时,系统将会发生质的变化(系统状态发生改变,从周期状态变为混沌的状态),所以在选取耦合系数时对实验仿真也至关重要。

图4 不同耦合系数系统的相图
3.2 频率ω对耦合系统的影响
ω代表周期策动力的频率,随着周期策动力的逐渐变化,系统的状态也在发生着变化,选择其它参数不变,即μ=0.8,c=0.8,f=0.343,k=0.5,选取ω=0.1,1.0,5.0,10.0时,分别观察系统的相图(如图5),仿真实验发现随着频率ω的改变,系统的状态发生了很大的变化。

图5 不同频率取值下系统的相图
综上所述,各个参数对于系统的影响还是比较大的,不合理参数的选取会对系统的状态发生本质的变化,所以在工程应用中,对于这个系统模型的应用,有待于进一步的探索,针对工程的需求,要合理地选择参数进行匹配,方可达到较好的效果。
4 Duffing和Van der Pol耦合振子在微弱信号检测中的应用分析
本节根据以上耦合振子的性质分析将其应用于微弱信号的检测,下面进行数值仿真实验,根据上面建立的耦合系统模型,选取k=0.8,c=0.5,μ=0.8,并且由以上实验分析得到的临界阈值f1=0.342,频率为1.0 rad/s作为周期信号和幅值为0.01的高斯白噪声信号一起加入进行数值仿真。数学模型如下
(3)
式中,fcos (ωt)为内置信号;acos (ωt)为待测的信号;σ(t)为高斯白噪声。对上述构造的系统进行仿真实验时, 选择从临界周期到周期的轨迹相变为判断系统输入是否带有谐波信号的依据, 亦即f1,f2将设置在临界分岔状态附近。当待测信号加入系统中经过暂态过程以后,系统稳定在某一运动形式上,计算机通过辨识系统容易得知系统是处于混沌还是大尺度周期运动状态。由此,可判断输入是纯噪声还是混有微弱周期信号。
当系统没有待测的周期的信号输入时,系统输出的呈现如图6(a)的混沌现象。当系统有相同的待测周期信号acos (ωt),其中a=0.001,输入系统时,系统输出的呈现如图6(b)的周期现象。

图6 噪声幅值为0.01时系统的相图
5 结论
本文研究了Duffing振子和Van der Pol振子的耦合特性,耦合系统的各个参数对系统动力学行为的影响,揭示了丰富的动力学特性。本研究发现在系统仿真求解的过程中,一个非线性微分方程的解与系统参数有很大的关系,通过仿真发现,此系统具有混沌现象和周期现象。我们也借此特性应用到微弱信号检测方面,表现出了比以往传统的微弱信号检测方法具有更好的稳定性和准确性。但由于Duffing振子和Van der Pol振子耦合系统具有更多的复杂性,仍是今后探索的地方。
[1]Han Y J. Dynamics of coupled nonlinear oscillators of different attractors; van der Pol oscillator and damped Duffing oscillator[J].Journal of the Korean Physical Society, 2000,37(1):3-9.
[2]李群宏,陆启韶.耦合Van der Pol-Duffing 振子的动力学分析[J].河南师范大学学报,2002,30(4):4-15.
[3]包刚,那仁满都拉,图布心,等.耦合混沌振子系统完全同步的动力学行为[J].物理学报, 2007,56(4):1971-04
[4]J Kengne, J C Chedjou, G Kenne,et al. Analog circuit implementation and synchronization of a system consisting of a van der Pol oscillator linearly coupled to a Duffing oscillator[J]. Nonlinear Dyn,2012,70:2163-2173
[5]催春夏,吴锋民.控制周期激VanderPol-Duffing 振子的混沌[J].浙江工业大学学报,2004, 32(3):6-18.
[6]李月,杨宝俊,石要武.色噪声背景下微弱正弦信号的混沌检测[J]. 物理学报, 2003, 48(1): 19-21.
[7]Li Yue,Lu Peng,Yang Baojun,et al.Applying a special kind of two coupled Duffing oscillator system to detect periodic signals under the background of strong colored noise[J].Phys.2006; 55(4): 1672-1677
[8]聂春燕.混沌系统与弱信号检测[M].北京:清华大学出版社,2009.
[9]代理,李健,郑豫,等. 基于双耦合Duffing 振子的随机相位正弦信号检测[J].成都信息工程学院学报,2008,23(1):50-53.
[10]李亚峻,李月,卢金,等.微弱信号混沌检测系统混沌阈值的确定[J].吉林大学学报,2004, 22(2):106-110.
[11]汪金山,汪晓东,施晓钟,等.基于Duffing混沌系统微弱信号检测的数值分析[J].仪器仪表学报,2005,26(8):33-34.
Analysis of Dynamical Behavior of a Van Der Pol Oscillator Coupled to a Duffing Oscillator
Wang Xiaodong1,2, Yang Shaopu1,2, Zhao Zhihong2
(1.School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2.Key Laboratory of Traffic Safety and Control in Hebei, Shijiazhuang 050043, China)
For complex dynamic behaviors of coupling nonlinear chaotic oscillators, this paper makes a Van der Pol oscillator couple to a duffing oscillator and establishes a duffing oscillator and Van der Pol oscillator coupling model, which, compared with the single oscillator, shows rich dynamics. With Simulink simulation method, by coupling the phase diagrams and Poincaré maps of nonlinear chaotic oscillators under different amplitudes of the driving motivation, different coupling coefficients and different frequencies, this paper analyzes the dynamics of coupling nonlinear oscillators, and studies the coupling oscillator sensitivity to the weak periodic signals and the immunity of noise and has applied this model in weak signal detection.
chaos; coupling oscillators; weak signal detection; simulation
2014-09-03 责任编辑:刘宪福
10.13319/j.cnki.sjztddxxbzrb.2015.04.10
王晓东(1989-)男,硕士研究生,研究方向为车辆的动力学控制与行为研究。E-mail:1099982864@qq.com
国家自然科学基金项目(11172182、11227201、11472179)王晓东,杨绍普,赵志宏.Duffing振子和Van der Pol振子耦合的动力学行为分析[J].石家庄铁道大学学报:自然科学版,2015,28(4):53-57,80.
TH165+.3
A
2095-0373(2015)04-0053-06

