(n,m)-强Ding投射模

张文汇， 姜泽博

(西北师范大学数学与统计学院，甘肃兰州 730070)

(n,m)-强Ding投射模

张文汇， 姜泽博

(西北师范大学数学与统计学院，甘肃兰州 730070)

引入了一类Ding投射维数有限的模，即(n,m)-强Ding投射模．证明了对任意非负整数m和正整数n，若M是(n,m)-强Ding投射模，则M的Ding投射维数不超过m．同时，考查了这类模的合冲的相关性质．

n-强Ding投射模；(n,m)-SD投射模；Ding投射维数

0 引言

1995年，Enochs等[1]在Gorenstein环上对任意模引入Gorenstein投射模的定义，推广了G-维数为0的有限生成模．目前，Gorenstein同调理论的发展已经取得了丰富的研究成果，同时也出现了许多新的模类，例如Ding投射模[2]．

称R-模M是Ding投射模，如果存在正合序列

使得以下条件成立：(1)对任意自然数i，Pi和Pi都是投射模；(2)M≅Im(P0→P0)；(3)对任意平坦模F，函子HomR(-,F)保持上序列的正合性．设n是任意正整数，称R-模M是n-强Ding投射模(简称n-SD投射模)[3]，如果存在R-模的正合序列

其中Pi(1≤i≤n)是投射模，并且对任意平坦模F，HomR(-，F)保持上述序列的正合性．设

是模M的任意一个投射分解，称Ki=Kerfi-1(1≤i≤n)为M的第i次合冲．

2007年，Bennis[4]引入了强Gorenstein投射模的概念，证明了Gorenstein投射模是强Gorenstein投射模的直和因子．2011年，Zhao-Huang[5]引入了n-强Gorenstein投射模的概念．2009年，Bennis[6]引入并研究了(n,m)-强Gorenstein投射模，这些模类都是强Gorenstein投射模类的推广．受以上文献的启发，本文引入并考查一类特殊的(n,m)-强Gorenstein投射模，我们称之为(n,m)-强Ding投射模．

本文环均指有单位元的结合环，除非特别声明，模均指左R-模，pd(M)和Dpd(M)分别表示模M的投射维数与Ding投射维数．

1 预备知识

引理1 设M和N是两个模，n是正整数．若M⊕P≅N⊕Q， 其中P,Q是投射模， 则M是n-强Ding投射模当且仅当N是n-强Ding投射模．

证明 由对称性只需证当M是n-强Ding投射模时，N是n-强Ding投射模．设M是n-强Ding投射模，则由文献[5]知M⊕P是n-强Ding投射模，于是存在正合列

其中Pi(1≤i≤n)是投射模，并且对任意平坦模F，函子HomR(-,F)保持上序列的正合性．由同构M⊕P≅N⊕Q知存在正合列

令Kn=Im(Pn→Pn-1)，K2=Im(P2→P1)，考虑推出图

由于N⊕Q是Ding投射模，故N是Ding投射模．又因为Kn是n-强Ding投射模，所以Kn是Ding投射模．由正合列

再考虑拉回图由第三行知Q1是投射模，于是将正合列

首尾相接便可得正合列

又由于上述三个序列都是HomR(-,F)正合的，故N是n-强Ding投射模． 】

命题1 设n是正整数，M是n-强Ding投射模,则以下结论成立：

(1)对任意正整数i，模M的第i次合冲是n-强Ding投射模；

(2)若

是模M的任意一个完全投射分解，则对任意整数i，Im(Pi→Pi-1)是n-强Ding投射模．

证明 (1) 由于M是n-强Ding投射模，所以存在正合列

其中Qi(i=0,1,…,n-1)是投射模，并且对任意平坦模F，上序列是HomR(-,F)正合的．

令Ki=Im(Qi→Qi-1)(i=1,2,…,n-1)，则有正合序列

将两序列首尾相接得正合列

且对任意平坦模F，序列HomR(-， F)是正合的．这说明Ki(i=1,2,…,n-1)是n-强Ding投射模．于是由引理1可知:对任意正整数i，M的第i次合冲是n-强Ding投射模．

(2)因为M是n-强Ding投射模，由(1)的证明知存在M的完全投射分解

使得每个同态的像Im(Qi→Qi-1)都是n-强Ding投射模．由文献[7]命题1.8及文献[8]习题3.37的对偶形式可得，在M的任意一个完全分解

中，Im(Pi→Pi-1)与Im(Qi→Qi-1)投射等价，于是由引理1可知Im(Pi→Pi-1)是n-强Ding投射模． 】

2 主要结果及证明

定义1 设m，n是整数，其中n≥1，m≥0，称M是(n,m)-强Ding投射模(简称为(n,m)-SD投射模)，如果存在正合列

注1 由定义1可知，强Ding投射模(简称SD投射模)是(1,0)-SD投射模．对任意正整数n，n-SD投射模是(n,0)-SD投射模； 投射维数不超过m的模是(n,m)-SD投射模．

引理2 设M是左R-模，m，n是整数，其中n≥1，m≥0，则下列结论成立：

(1)设M是(n,m)-SD投射模．对任意整数m′，若m′≥m，则M是(n,m′)-SD投射模；

(2)设M是(n,m)-SD投射模，k是任意正整数，则M是(kn,m)-SD投射模． 特别地， 每个(1,m)-SD投射模都是(n,m)-SD投射模．

证明 (1) 显然．

(2)因为M是(n,m)-SD投射模，所以存在如下正合列

引理3 (n,m)-SD投射模类关于直和封闭．

定理1 设整数n≥1，m≥0，M是(n,m)-SD投射模,则

(1)存在非负整数k使得Dpd(M)=k≤m；

(2)模M的第i(1≤i≤k)次合冲是(n,m-i)-SD投射模；

(3)模M的第i(i≥k)次合冲是(n,0)-SD投射模．

证明 先证明(1)和(2)．由M是(n,m)-SD投射模可知存在正合列

其中pd(Qi)≤m，1≤i≤n，且对任意平坦模F，

考虑M的投射分解

分解为短正合列

其中Hn=M=H0，Hi=Ker(Qi→Hi-1)，i=1,2,…,n-1．

对Hi(i=0,1,…,n)，考虑短正合列

其中Pi,0(i=1,2,…,n-1)是投射模．令Pn,0=P0,0=P0，Kn,1=K0,1=K1，由马掌引理可得交换图

其中1≤i≤n，再将这n-1个图粘接，可得行正合变换图

(3)首先考虑M的第k次合冲Kk， 由Kk是Ding投射模，所以任取Kk的一个投射分解作为其完全投射分解的左半部分，可得正合列

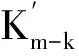
其中Li(1≤i≤n)是投射模.因为Kk是Ding投射模,故对任意整数i>0及任意平坦模F，

这说明Kk是(n，0)-SD投射模．由命题1及(n,0)-SD投射模的定义可知，对任意i≥k，M的第i次合冲是(n,0)-SD投射模． 】

命题2 设M和N是模，若M⊕P≅N⊕Q， 其中P和Q具有有限的投射维数，整数n≥1，m=max{pd(P)，pd(Q)}，则M是(n,m)-SD投射模当且仅当N是(n,m)-SD投射模．

证明 由对称性只需证当M是(n,m)-SD投射模时，N是(n,m)-SD投射模即可． 由注1知P和Q都是(n,m)-SD投射模，于是当M是(n,m)-SD投射模时，由引理4可知直和M⊕ P≅N⊕Q是(n,m)-SD投射模．令H=N⊕Q，则存在正合列

下证N是(n,m)-SD投射模，将上述正合列分解为三个正合序列

注意到有可裂的短正合列

考虑同态f与g的推出及l与h的拉回

由定理1(1)可知H,E,F的Ding投射维数都小于等于m，故由以上两图知G1和Gn有有限的Ding投射维数且小于等于m．又由两图的中间列可知G1和Gn有有限的投射维数，所以

pd(G1)=Dpd(G1)≤m，

pd(Gn)=Dpd(Gn)≤m．

由正合列

可得正合列

定理2 设M为左R-模，整数n≥1，m≥0，则下列结论成立:

(1)若M既是Ding投射模又是(n,m)-SD投射模，则它是(n,0)-SD投射模；

(2)若M的第d(d≥1)次合冲是(n,m)-SD投射模，则存在正整数k，使得Dpd(M)=k≤d+m，且M的第i(i≥k)次合冲是(n,0)-SD投射模．

证明 (1) 类似于定理1(3)中Kk是(n,0)-SD投射模的证明．

(2) 因为M的第d(d≥1)次合冲是(n,m)-SD投射模，所以存在正整数k，使得Dpd(M)=k≤d+m．于是存在正合列

其中Pi(0≤i≤k-1)是投射模， Kk是Ding投射模.考虑Kk的完全投射分解的左半部分

其中Qk+i为投射模(i=0,1,…,d-k-1)，Kd为Ding投射模．注意到Kd是M的第d次合冲，由命题2及M的任意两个第i次合冲投射等价可知 Kd是(n,m)-SD投射模． 由(1)知Kd是(n,0)-SD投射模，又由命题1知Kd的第i次合冲是n-SD投射模，并且它与M的第k+i次合冲投射等价， 再利用命题1可知M的第i(i≥k)次合冲是(n,0)-SD投射模. 】

[1]ENOCHSEE,JENDAOMG.Gorensteininjectiveandprojectivemodules[J].Math Z,1995,220(1):611-633.

[2] DING N Q, LI Y L,MAO L X.Strongly Gorenstein flat modules[J].JAustMathSoc,2009,86(3)：323-338.

[3] LIU Y P.A generalization of strongly Ding projective modules[J].兰州大学学报:自然科学版,2012,48(2):101-105.

[4] BENNIS D,MAHDOU N.Strongly Gorenstein projective,injective,and flat modules[J].JAlgebraAppl,2007,210(2)：437-445.

[5] ZHAO G Q,HUANG Z Y.n-strongly Gorenstein projective,injective and flat modules[J].CommAlgebra,2011,39(8)：3044-3062.

[6] BENNIS D.(n,m)-strongly Gorenstien projective modules[J].IternaltionalElectronicJournalofAlgebra,2009,6:119-133.

[7] HOLM H.Gorenstien homological dimensions[J].JPureAlgebra,2004,189(1-3)：167-193．

[8] ROTMAN J J.AnIntroductiontoHomologicalAlgebra[M].New York:Academic Press,1979．

(责任编辑 马宇鸿)

(n,m)-stronglyDingprojectivemodules

ZHANGWen-hui，JIANGZe-bo

(CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,Gansu,China)

A class modules of having finite Ding projective dimension are investigated in this paper,namely the (n,m)-strongly Ding projective modules．For nonnegative integralmand positive integraln,Ding projective dimension ofMis not larger thanmifMis (n,m)-strongly Ding projective module.At the same time,the homological properties of syzygy are discussed for the modules.Key words:n-strongly Ding projective modules;(n,m)-SD projective modules;Ding projective dimensions

2015-03-19;修改稿收到日期:2015-04-20

国家自然科学基金资助项目(11201376)

张文汇(1977—)，女，甘肃天水人，副教授，博士，硕士研究生导师.主要研究方向为环的同调理论． E-mail:zhangwh@nwnu.edu.cn

O

A

1001-988Ⅹ(2015)04-0021-05