关于H-矩阵的预条件AOR迭代法的收敛性探讨

李 斌

(湖南科技学院 理学院, 湖南 永州 425100)

关于H-矩阵的预条件AOR迭代法的收敛性探讨

李 斌

(湖南科技学院 理学院, 湖南 永州 425100)

利用矩阵迭代理论与比较定理, 分析了线性方程组的系数矩阵为H-矩阵时, 预条件后AOR迭代法的收敛性;并给出了当加速因子γ不变时, 松弛因子ω的大小与收敛速度的关系; 同时还给出了两个数值实例验证了主要的结论.

预条件; AOR迭代法; Gauss-Seidel迭代法; M-矩阵

考虑线性方程组

这里A=(aij)∈ℝn×n是非奇异矩阵, b∈ℝn×1,x∈ℝn×1. 若A=M-N, 其中M, N∈ℝn×n, 并且M是非奇异的, 则分裂迭代法可以表示为

不失一般性, 假设A为对角元全为1的方阵, 且

其中I, -L, -U分别是A的对角, 严格下三角和严格上三角部分, 则线性方程组(1)的AOR迭代法的迭代矩阵为

其中0≤γ≤ω≤1,ω≠0.

为了更好地求解方程组(1), 我们引入各种各样的非奇异预条件矩阵P来加快迭代矩阵的收敛速度.文[1]提出了一种更一般的预条件P=I+P1+P2, 它可以和A所有的元素有联系.

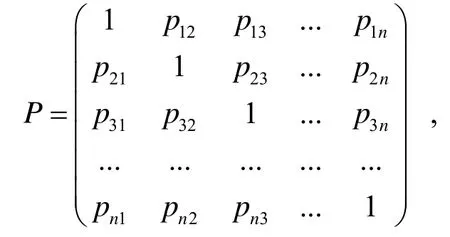
其中I, P1, P2分别是预条件矩阵P的对角部分、严格下三角矩阵和严格上三角矩阵. 对线性方程组(1)实行预条件P=I+P1+P2后, 线性方程组(1)变为

1 相关引理和定义

定义1.1[1]设A=(aij)∈ℝn×n, 且aij≤0(i≠j, i, j=1,2,…,n), 则称A为Z-矩阵. 如果A为非奇异的Z-矩阵, 且A-1≥0, 则称A为M-矩阵.

定义1.2[2]设A=(aij)∈ℝn×n, 则称A=M-N为矩阵A的一个分裂, 其中M为非奇异矩阵. 分别称A=M-N为矩阵A的

(1) 收敛分裂, 如果ρ(M-1N )＜1;

(2) 正则分裂, 如果M-1≥0, 且N≥0;

(3) 弱正则分裂, 如果M-1N≥0;

(4) M-分裂, 如果M为非奇异M-矩阵, 且N≥0.

引理1.1[1]设A=(aij)∈ℝn×n为非奇异的M-矩阵, 如果P=(pij)≥0是一个非奇异的矩阵, 且满足pii=1,i=1,2,…,n,≤0,1≤i≠j≤n, 则PA也是一个非奇异的M-矩阵.

引理1.2[1]设A=(aij)∈ℝn×n为非奇异的H-矩阵. 如果P=(pij)≥0是一个非奇异的矩阵, 且满足pii=1,i=1,2,…,n ,≤0,1≤i≠j≤n, 则PA也是一个非奇异的H-矩阵.

引理1.3[3]设A是一个Z-矩阵, 则下列说法是等价的:

(a) A是一个非奇异的M-矩阵;

(b) 存在一个矢量x＞0, 使得Ax＞0;

(c) 任何弱正则分裂是收敛的.

引理1.4[3]若A是非负矩阵, 则

(a) 如果αx≤Ax , 对某一个非负的向量x且x≠0成立, 则α≤ρ(A);

(b) 如果Ax≤βx对某一个正向量x成立, 则ρ(A)≤β. 进一步, 如果A是不可约的, 且若有0≠αx≤Ax≤βx , αx≠Ax 和Ax≠βx对某一个非负的向量x成立, 则α＜ρ(A)＜β, 且x是一个正向量.

引理1.5[4]若A≥0是矩阵, 则

(a) A有一个非负的实特征值等于它的谱半径;

(b)ρ(A)对应的特征向量x≥0, 且x≠0;

(c) 当A的任何元素增大, ρ(A)不减.

定理1.1[1], 设A=(aij)∈ℝn×n是一个非奇异的Z-矩阵, 若对∀0≤γ≤ω≤1,ω≠0, P=(pij)≥0是一个的非奇异的矩阵, 且pii=1,i=1,2,…,n ,1≤i≠j≤n, 则

(a) 如果ρ(Tγ,ω)＜1, 则

(b) 如果ρ(Tγ,ω)＞1, 且P满足1≤i≤n , 则

2 预条件后的AOR迭代方法

定理2.1设A=(aij)∈ℝn×n是一个非奇异的M-矩阵. 假设 0≤γ≤ω≤1,ω≠0,P=(pij)≥0是一个非奇异的矩阵, pii=1,i=1,2,…,n , pij满足下面的条件之一:

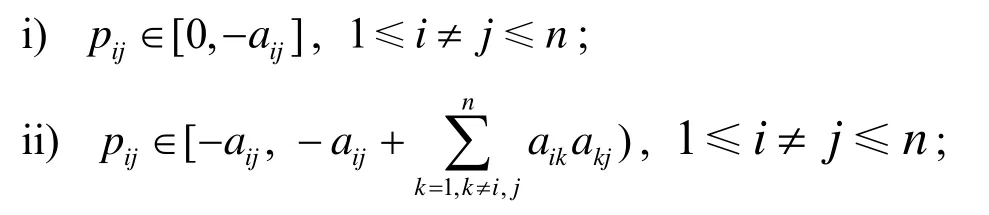
证明1) 当pij满足条件i)时, 由文献[1]的定理2.7可知, 结论成立.

2) 当pij满足条件ii)时, 因A是一个非奇异的M-矩阵, 由引理1.3知ρ(Tγ,ω)＜1.

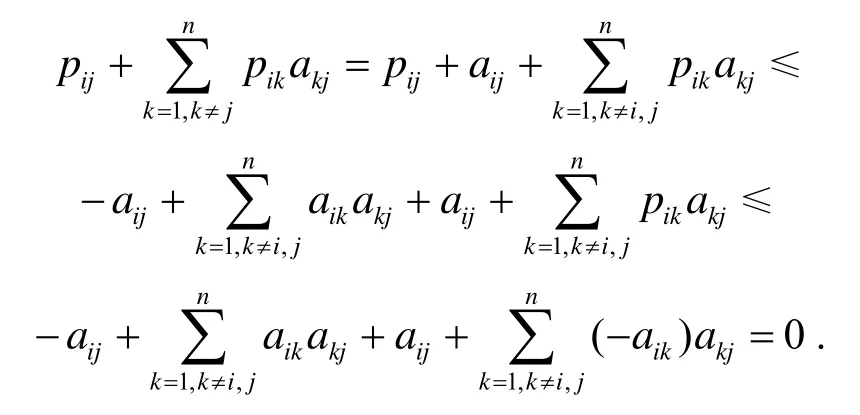
注:定理2.1在保持结论不变的情况下对文[1]的定理2.7的预条件矩阵P的取值范围进行了推广.

定理2.2设A=(aij)∈ℝn×n是一个H-矩阵. 假设0≤γ≤ω≤1,ω≠0,P=(pij)≥0是一个非奇异的预条件矩阵, 且pii=1,i=1,2,…,n ,

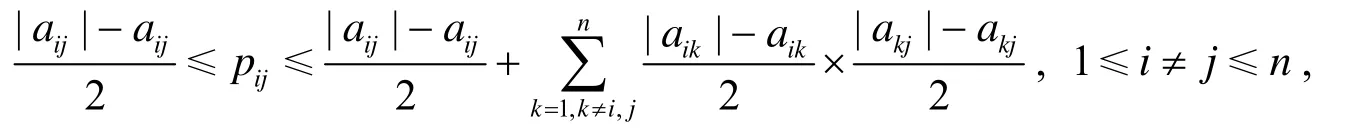
则PA也是一个H-矩阵.

证明注意到

由引理1.2知, PA也是一个H-矩阵.

定理2.3设A=(aij)∈ℝn×n是一个H-矩阵. 假设0≤γ≤ω≤1,ω≠0,P=(pij)≥0是一个非奇异的预条件矩阵, 且

则有

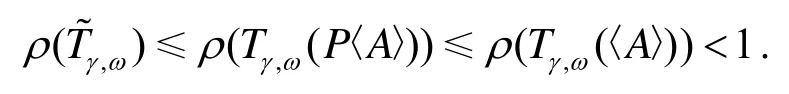
这里Tγ,ω(B)代表矩阵B所对应的AOR迭代矩阵.

证明A是一个H-矩阵, 则〈A〉是一个非奇异的M-矩阵, 故由引理1.3有ρ(Tγ,ω〈(A〉 ))＜1.

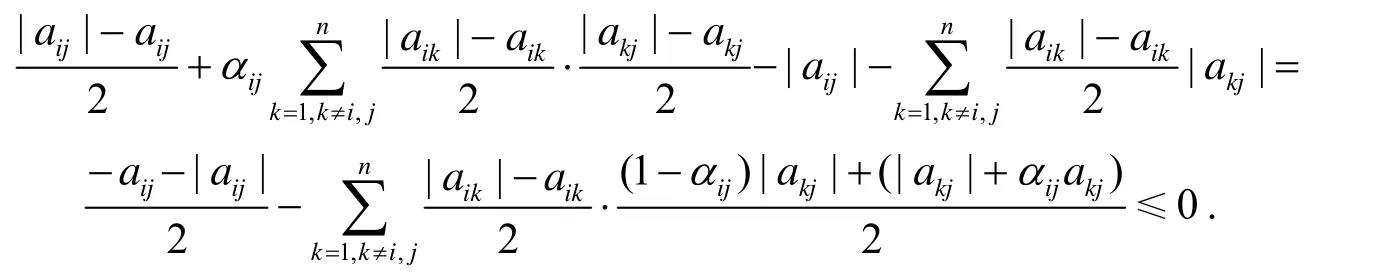
由引理1.1知P〈 A〉也是一个非奇异的M-矩阵, 因此, 由文[1]定理2.1, 有

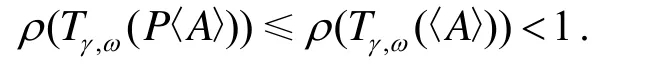
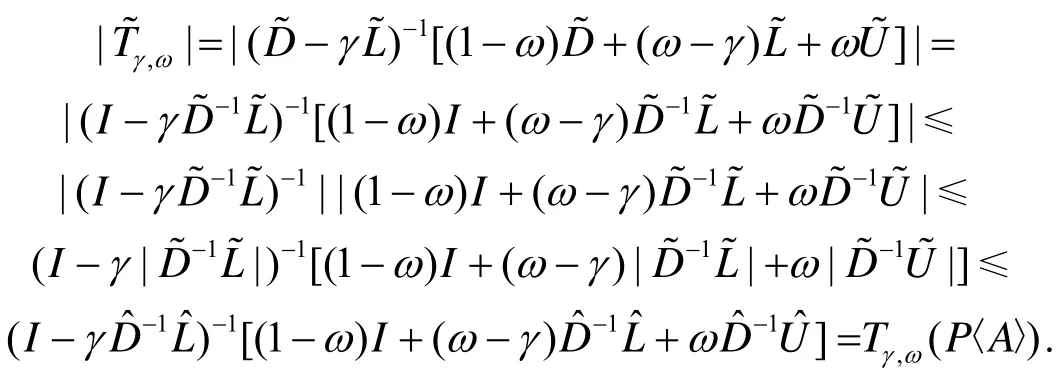
定理2.4设A=(aij)∈ℝn×n是一个H-矩阵. 假设0≤γ≤ω2≤ω1≤1,ωi≠0,i=1,2, P=(pij)≥0是一个非奇异的预条件矩阵, 且满足定理2.3的条件, 则有

证明根据已知条件, 由定理2.3有

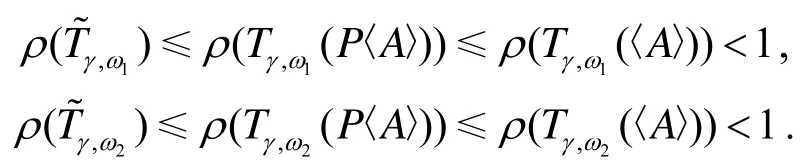
下面证明, ρ(Tγ,ω1P〈 A〉)＜ρ(Tγ,ω2P〈 A〉 ).

事实上, 由于P〈 A〉是非奇异的M-矩阵, 易得Tγ,ω2(P〈 A〉 )≥0. 结合引理1.5知, 存在向量x≥0, 且x≠0,Tγ,ω2P〈 A〉 x=ρ(Tγ,ω2P〈 A〉)x . 不妨设ρ(Tγ,ω2P〈 A〉 )=λ, 有ρ(Tγ,ω2P〈 A〉) x=λx , 即

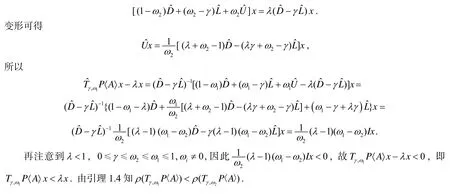
3 数值试验

例 设

由于A的比较矩阵〈A〉是一个M-矩阵, 故A为H-矩阵. 表1反映的是定理2.3中, 当αij=0时, 谱半径的大小情况; 表2反映的是定理2.4中, 当γ不变, ω增大时, 谱半径的大小情况, 从而验证了结论的正确性.

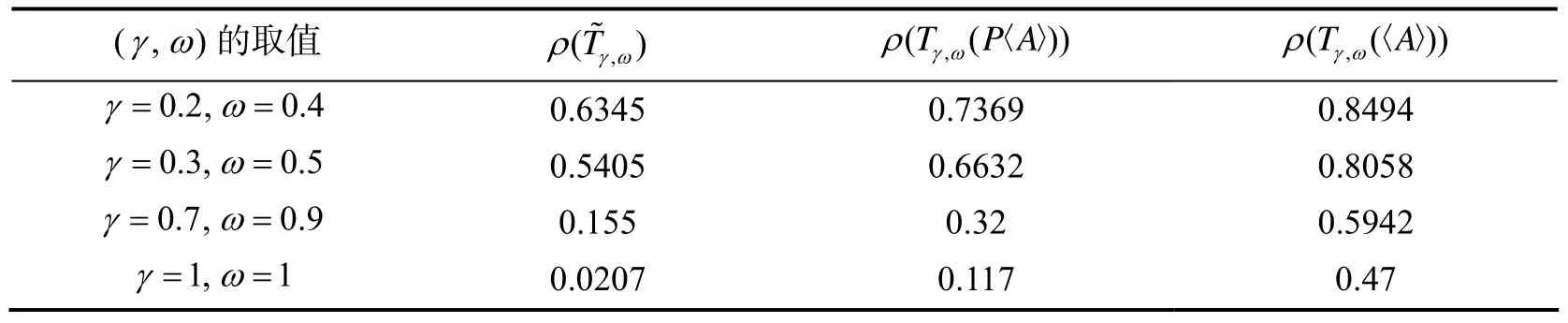
表1 不同条件下AOR迭代法的谱半径

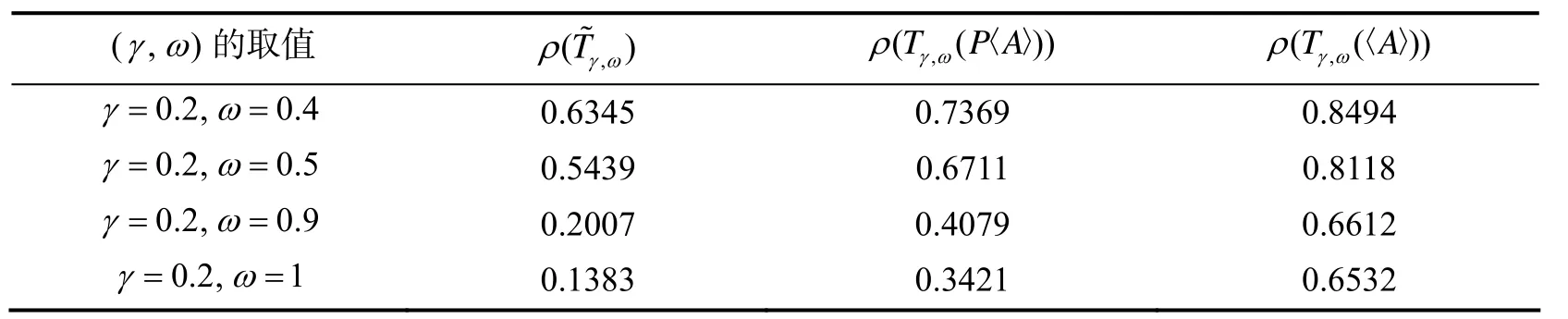
表2 在γ不变, ω增大的条件下AOR迭代法的谱半径

[1] L.Wang, Y.Song. Preconditioned AOR iterative methods for M-matrices[J]. J.Comput.Appl. Math. 2009, 226: 114～124

[2] RICHARD S VARGA. Matrix iterative analysis[M]. Heidelberg. Spring-Verlag, 2000: 89～121

[3] A.Berman, R.J. Plemmons. Nonnegative Matrices in the Mathematical Sciences[M]. Academic Press, New York, 1979, SIAM, Philadelphia, PA, 1994

[4] R.S.Varga. Matrix Iterative Analysis[M]. Prentice-Hall, Englewood Cliffs, NJ, 1962; Springer Series in Computational Mathematics, vol. 27, Springer-Verlag, Berlin, 2000

[5] A. Frommer. D.B.Szyld, H-splitting and two-stage iterative methods[J]. Numer. Math. 1992, 63: 345～356

[6] 程云鹏. 矩阵论[M]. 西安: 西北工业大学出版社, 2004

The Convergence Discussion of the AOR Precondition Iterative Methods for H-matrices

LI Bin
(College of Science, Hunan University of Science and Engineering, Yongzhou 425100, China)

This paper firstly presents the convergence analysis of AOR-type iterative method for solving linear systems with H-matrices by using matrix iterative analysis and comparison theorems; then gets the relations between the size of relaxation factorωand the rate of convergence when the acceleration factor γis constant. Finally, the author verifies his conclusions through two numerical examples.

precondition; AOR-type iterative method; Gauss-Seidel iterative method; M-matrix

O151.21

: A

1672-5298(2015)03-0012-05

2015-07-01

湖南科技学院教学改革研究项目(湘科院教字[2014]14号)

李 斌(1973- ), 男, 湖南双峰人, 硕士, 湖南科技学院理学院讲师. 主要研究方向: 计算数学