矩阵对角化在图谱理论中的应用

杜志斌

摘 要 矩阵对角化是高等代数中的一个重要内容，其在矩阵研究中起着非常重要的作用。图谱理论主要运用线性代数方法来研究图的各种性质。本文将给出矩阵对角化在图谱理论中的一个应用。

关键词 矩阵对角化 图谱 特征值重数

中图分类号：O151.21 文献标识码：A DOI：10.16400/j.cnki.kjdkx.2015.07.027

Application of Diagonalization of Matrices in Spectral Graph Theory

DU Zhibin

（School of Mathematics and Statistics， Zhaoqing University， Zhaoqing， Guangdong 526061）

Abstract Diagonalization of matrices is an important part in higher algebra， which plays an important role in the research of matrices. Spectral graph theory mainly uses the methods related to linear algebra to study various properties of graphs. In this paper， we will present an application of diagonalization of matrices in spectral graph theory.

Key words diagonalization of matrices; spectra of graphs; multiplicity of eigenvalues

0 引言

记为阶单位矩阵。对于任意实对称阵，若是的一个特征值，则记（）为的（代数）重数。此外，若不是的特征值，则习惯上记作（） = 0。

矩阵对角化是高等代数中的一个重要内容，其在矩阵研究中起着非常重要的作用。特别地，若阶矩阵可对角化，则对于任意常数，总有

秩（） = （）    （1）

参见[1]。

本文将给出矩阵对角化在图谱理论中的一个应用。所谓图谱理论，它主要运用线性代数方法来研究图的各种性质。

作为数与形相互结合的一个典范，图与矩阵有着紧密的联系。给定一个图，可定义出一些相应的矩阵，如邻接矩阵、Laplacian矩阵等。通过研究这些由图所导出的矩阵的特征多项式、特征值、特征向量等，学者们得到了一大批精彩的新理论和结果，并由此建立了图谱理论。

在图谱理论的研究中，研究的核心内容之一是基于图所导出的各类矩阵的特征值，其中以图的邻接矩阵的研究尤为突出。

本文所考虑的图皆为无向简单图。图的邻接矩阵（）定义为[2]：

图的邻接矩阵的特征值简称为图的特征值，由这些特征值所组成的多重集称为图的邻接谱。

显然图的邻接矩阵是一个实对称阵，从而它可对角化。于是，我们很自然地提出一个问题：矩阵对角化的知识是否可运用到图的邻接谱的研究中。答案是肯定的。本文将给出矩阵对角化在计算图的邻接谱中的一个应用。

1 矩阵对角化在计算图的邻接谱中的应用

现有图以及阶方阵 = （）。若将图的点集划分为个点子集，，…，，且使得中的每个点都与中的个点相邻，其中， = 1，2，…，，则称为图的因子（divisor）。特别地，若为图的因子，根据[2，定理4.5]，的特征值同时也是图的邻接矩阵（）的特征值。

下面我们将运用矩阵对角化（即式子（1））来计算一些具有低阶因子（即因子阶数为 = 2，3）的图的邻接谱。特别地，对于因子阶数为 = 2的情形，我们定义了一类图——完全分割图（complete split graph），而对于因子阶数为 = 3的情形，我们定义了另一类图——广义完全分割图。

记为行列零矩阵，且记为一个行列矩阵，其中每个元素皆为1。特别地，若 = ，则将简记为，而将简记为。

1.1 完全分割图的邻接谱

所谓完全分割图（，）即为 ，其中表示个点的完全图，表示个点的空图，而 表示中的每个点与中的每个点皆为相邻的。例如，图1所示即为完全分割图（5，2）。

图1 完全分割图（5，2）

我们不妨将（，）中的点划分为两部分，，其中是（，）的头个点，对应着完全图，而剩余的个点记作，对应着空图。此外，为了方便起见，令 = （（，））。

易见，图存在一个2阶因子

即该矩阵的2个特征值亦为的特征值。对于剩余的个特征值，我们将利用式子（1）来求得。

首先，根据完全分割图（，）的构造及其点的编号，可知其邻接矩阵的结构如下：

显然有秩（0） = 秩（） = + 1。现根据（1），可得（0） = 。

另一方面，由于

从而有秩（ + ） = + 1。现根据（1），可得（） = 。

综上所述，我们可求得完全分割图（，）的邻接矩阵的所有特征值。

1.2 广义完全分割图的邻接谱

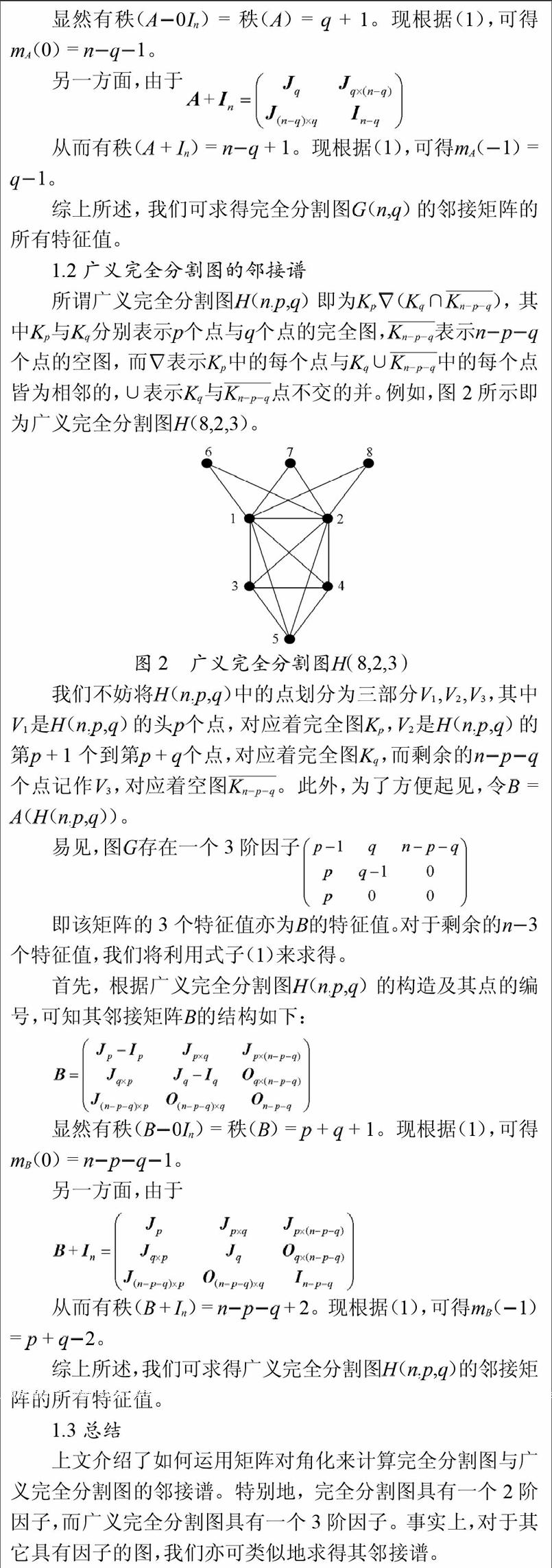
所谓广义完全分割图（，，）即为 （∩），其中与分别表示个点与个点的完全图，表示个点的空图，而 表示中的每个点与∪中的每个点皆为相邻的，∪表示与点不交的并。例如，图2所示即为广义完全分割图（8，2，3）。

图2 广义完全分割图（8，2，3）

我们不妨将（，，）中的点划分为三部分，，，其中是（，，）的头个点，对应着完全图，是（，，）的第 + 1个到第 + 个点，对应着完全图，而剩余的个点记作，对应着空图。此外，为了方便起见，令 = （（，，））。

易见，图存在一个3阶因子

即该矩阵的3个特征值亦为的特征值。对于剩余的个特征值，我们将利用式子（1）来求得。

首先，根据广义完全分割图（，，）的构造及其点的编号，可知其邻接矩阵的结构如下：

显然有秩（0） = 秩（） = + + 1。现根据（1），可得（0） = 。

另一方面，由于

从而有秩（ + ） = + 2。现根据（1），可得（） = + 。

综上所述，我们可求得广义完全分割图（，，）的邻接矩阵的所有特征值。

1.3 总结

上文介绍了如何运用矩阵对角化来计算完全分割图与广义完全分割图的邻接谱。特别地，完全分割图具有一个2阶因子，而广义完全分割图具有一个3阶因子。事实上，对于其它具有因子的图，我们亦可类似地求得其邻接谱。

此外，在图谱理论的研究中，图的Laplacian矩阵[4]、无符号Laplacian矩阵[5]、正规化Laplacian矩阵[6]、距离矩阵[7]等基于图所导出的矩阵的谱也是关注的热点。类似于上述方法，我们亦可求得这些基于图所导出的矩阵的谱。

参考文献

[1] 张和瑞，郝鈵新.高等代数[M]（第五版）.北京：高等教育出版社，2007.

[2] D.Cvetkovi， M. Doob， H. Sachs， Spectra of Graphs-Theory and Application[M]. New York： Academic Press，1980.

[3] A.E. Brouwer， W.H. Haemers， Spectra of graphs[M].New York： Springer，2012.

[4] R.Grone， R.Merris， The Laplacian spectrum of a graph II[J].SIAM J.Discrete Math.，1994.7：221-229.

[5] D.Cvetkovi， P. Rowlinson， S.K. Simi， Eigenvalue bounds for the signless Laplacian[J]. Publ. Inst. Math. （Beograd）， 2007.81：11-27.

[6] F. R. K. Chung， Spectral Graph Theory[M].Providence： American Math. Soc.， 1997.

[7] R. Merris， The distance spectrum of a tree[J].J. Graph Theory，1990.14：365-369.