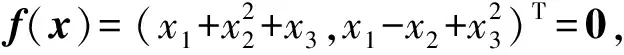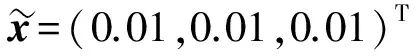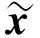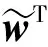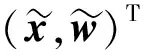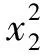欠定非线性系统极小二范数解的可信误差界
李 喆,桑海风,徐维华
(1.长春理工大学 理学院,长春 130022;2.自动推理与认知重庆市重点实验室,重庆 400714;3.符号计算与知识工程教育部重点实验室,长春 130012;4.北华大学 数学与统计学院,吉林 吉林 132013)
欠定非线性系统极小二范数解的可信误差界
李 喆1,2,3,桑海风4,徐维华1
(1.长春理工大学 理学院,长春 130022;2.自动推理与认知重庆市重点实验室,重庆 400714;3.符号计算与知识工程教育部重点实验室,长春 130012;4.北华大学 数学与统计学院,吉林 吉林 132013)
考虑欠定非线性系统极小二范数解的可信验证问题.欠定非线性系统的极小二范数解为解向量二范数的极小值点,对给定的欠定非线性系统,将方形非线性系统单根的可信验证方法与对称正定矩阵的可信验证方法相结合,给出计算Jacobi矩阵为列满秩欠定非线性系统极小二范数解的可信误差界算法.
欠定系统;极小二范数解;可信验证
0 引 言
所谓可信验证,就是对给定的非线性求解问题,给出该问题的一个近似解及其相应的误差界,使得在近似解的误差界范围内一定存在一个精确解.Rump[1]给出了系数阵为一般稠密矩阵的线性方形系统求解的可信性验证方法.该算法写入在MATLAB中的INTLAB软件包中,命名为Verifylss函数.对于系数阵为区间矩阵的线性系统,Verifylss函数输出一个区间向量,该区间向量包含该区间线性系统的所有可能解.对于欠定线性系统,Rump[2]给出了计算极小二范数解的可信误差界的算法.给定A∈n×m,n ‖A+b‖=min{‖x‖2:Ax=b}, 其中A+为A的广义逆矩阵.Rump通过计算增广系统 零点的可信误差界得到了欠定系统Ax=b极小二范数解的可信误差界.Rump的方法不仅适用于系数阵稠密的线性系统,对于系数阵稀疏的线性系统也有效.Miyajima[3]给出了欠定线性系统极小二范数解的算法,并证明了该算法得到的可信逐点误差界每个分量都小于等于Rump[2]给出的算法.之后,Rump[4]又利用给定的近似值误差界,改进了Miyajima[3]的方法,该方法并未提高Miyajima方法的精度,但给出了Miyajima方法一个很好的表示形式,这个表示形式适用于数值计算的可信验证. Moore[5]给出了非线性系统单根存在的充分条件,在此基础上,Krawczyk[6]将牛顿迭代法应用于区间计算,以此验证非线性系统的单根.Rump[7]改善了区间牛顿迭代法使其能更好地实际应用,提出了非线性系统单根的可信验证定理,并在INTLAB软件中实现,命名为Verifynlss函数. 文献[8-11]讨论了欠定非线性系统零点的数值算法,文献[12]通过将欠定非线性系统的某些变元特定化,给出了欠定非线性系统零点的可信验证算法.但目前还没有针对欠定非线性系统极小二范数解的可信性验证算法.本文考虑欠定非线性系统极小二范数解的可信误差界计算,将欠定非线性系统极小二范数解的计算转化为优化问题的稳定点计算,利用方形非线性系统的单根可信验证方法计算优化问题稳定点的可信误差界,利用对称正定矩阵的可信验证方法判断稳定点是否为极值点. 设A为区间对称矩阵,若对其中任意一个实对称矩阵都正定,则称区间对称矩阵A正定. 引理1[13]给定对称矩阵M,R∈n×n,令Σ=[M-R,M+R]∈In×n.如果存在c∈,使得‖R‖2≤c且M-cI为正定阵,则所有实对称矩阵A∈Σ正定. 定理1[7]设函数f:n→n,其中f=(f1,…,fn)∈C1.给定初始近似解n,初始区间X∈In,且0∈X,R∈n×n.设区间矩阵M∈In×n满足条件⊆Mi,:.若 设f:n→m,f=(f1,…,fm)T,n>m,其中f1,…,fm具有二阶连续偏导数.欠定非线性系统f(x)=0的极小二范数解为约束优化问题 (1) 的极小值点.引入Lagrange乘子w=(w1,…,wm)T,构造Lagrange函数 (2) 则L(x,w)的稳定点为条件极值(1)的可能极值点.L(x,w)的稳定点为系统 (3) 的零点,其中Jf(x)为系统f(x)=0的Jacobi矩阵. 命题1[1]设f:n→m,f=(f1,…,fm)T,n>m,其中f1,…,fm具有二阶连续偏导数.对于系统L(x,w)=0,给定其近似解若Verifynlss函数能成功计算出包含该系统真解的区间向量(X,W)T,则f(x)=0在的Jacobi矩阵行满秩. 其中M(x,w)的第i行第j列元素为 (4) 因此,条件极值(1)的极小值点等价于函数 (5) 的极小值点. 令Hg(x(1))表示g(x(1))的Hessian矩阵,则 (6) 下面计算Hg(x(1)).对非线性系统f(x(1),h(x(1)))=0关于每个自变量xi(1≤i≤n-m)求导可得 (7) 再对系统(7)关于每个自变量xj(1≤j≤n-m)求导可得 (8) 因此,令x=X,利用Verifylss函数求解线性系统(7),(8),可得区间向量U(i),U(i,j)(1≤i≤j≤n-m),使得 利用U(i),U(i,j)可得到区间对称矩阵H,使得H⊇Hg(X(1)). 算法1 输入: 1)f(x)=0(m个方程n个变元的具有二阶连续偏导数的欠定非线性系统); 2)数值秩容差ε1; 3)数值迭代容差ε2; 4)最大迭代次数N; 输出: 2)或者“失败”. 步骤: 1)初始iter=0. 3)初始iter=0. 4)区间牛顿迭代. ② 如果Verifynlss函数运行不成功,则返回“失败”,算法终止. 5)验证Hessian矩阵的正定性. ① 选取in-m+1<… ④ 利用Isspd函数验证Hg(X(1))的正定性,如果成功,则返回X=X1:n;否则,返回“失败”. 2)计算得 4)计算包含系统 的零点区间向量: 5)令X(1)=X1,X(2)=(X2,X3)T,则区间矩阵Jf(X):,2:3为可逆区间矩阵,根据式(6),计算Hessian阵为 Hg(X(1))=[5.999 999 999 999 99,6.000 000 000 000 01]. 利用INTLAB软件中的Isspd函数可验证Hg(X(1))为正定矩阵,故 为包含欠定系统f(x)=0极小二范数解的可信区间. [1] Rump S M.Kleine Fehlerschranken Bei Matrixproblemen [D].Karlsruhe:Universit Karlsruhe,1980. [2] Rump S M.Verified Bounds for Least Squares Problems and Underdetermined Linear Systems [J].SIAM J Matrix Anal Appl,2012,33(1):130-148. [3] Miyajima S.Componentwise Enclosure for Solutions in Least Squares Problems and Underdetermined Systems [J].Linear Alger Appl,2014,444:28-41. [4] Rump S M.Improved Componentwise Verified Error Bounds for Least Squares Problems and Underdetermined Linear Systems [J].Numer Algor,2014,66(2):309-322. [5] Moore R E.A Test for Existence of Solutions to Nonlinear System [J].SIAM J Numer Anal,1977,14(4):611-615. [6] Krawczyk R.Newton-Algorithmen Zur Bestimmung Von Nullstellen Mit Fehlerschranken [J].Computing,1969,4(3):187-201. [7] Rump S M.Solving Algebraic Problems with High Accuracy [C]//Proceedings of the Symposium on a New Approach to Scientific Computation.San Diego:Academic Press,1983:51-120. [8] Meyn K H.Solution of Underdetermined Nonlinear Equations by Stationary Iteration Methods [J].Numer Math,1983,42(2):161-172. [9] Walker H F,Watson L T.Least-Change Secant Update Methods for Underdetermined Systems [J].SIAM J Numer Anal,1990,27(5):1227-1262. [10] Martínez J M.Quasi-Newton Methods for Solving Underdetermined Nonlinear Simultaneous Equations [J].J Comput Appl Math,1991,34(2):171-190. [11] CHEN Xiaojun,Yamamoto T.Newton-Like Methods for Solving Underdetermined Nonlinear Equations with Nondifferentiable Terms [J].J Comput Appl Math,1994,55(3):311-324. [12] CHEN Xiaojun,Womersley R S.Existence of Solutions to Systems of Underdetermined Equations and Spherical Designs [J].SIAM J Numer Anal,2006,44(6):2326-2341. [13] Rump S M.Verification Methods:Rigorous Results Using Floating-Point Arithmetic [J].Acta Numer,2010,19:287-449. (责任编辑:赵立芹) VerifiedErrorBoundsforMinimum2-NormSolutionsofUnderdeterminedNonlinearSystems LI Zhe1,2,3,SANG Haifeng4,XU Weihua1 (1.SchoolofScience,UniversityofScienceandTechnology,Changchun130022,China;2.AutomatedReasoningandCognitionKeyLaboratoryofChongqing,Chongqing400714,China;3.KeyLabofSymbolicComputationandKnowledgeEngineeringofMinistryofEducation,Changchun130012,China;4.CollegeofMathematicsandStatistics,BeihuaUniversity,Jilin132013,JilinProvince,China) This paper deals with the verification for minimum 2-norm solutions of underdetermined nonlinear systems.The minimum 2-norm solution of underdetermined nonlinear system is the minimum point of the 2-norm of solution vectors.For the given undetermined nonlinear system,combining the verification for simple solutions of square systems with the verification for symmetric positive definite matrices presented an algorithm for verifying minimum 2-norm solutions of underdetermined nonlinear systems with full rank Jacobian matrices. underdetermined system;minimum 2-norm solution;verification 10.13413/j.cnki.jdxblxb.2015.03.12 2014-10-13. 李 喆(1981—),女,汉族,博士,讲师,从事计算机代数的研究,E-mail:zheli200809@163.com.通信作者:桑海风(1982—),男,汉族,博士,讲师,从事计算机代数的研究,E-mail:sanghaifeng2008@163.com. 国家自然科学基金(批准号:11326209;11171133;91118001)和自动推理与认知重庆市重点实验室开放课题基金(批准号:CARC2014002). O241.3 :A :1671-5489(2015)03-0414-051 预备知识
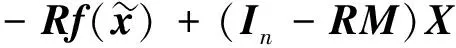
2 主要结果
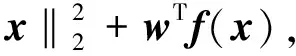
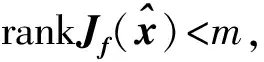
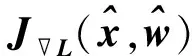

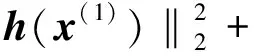
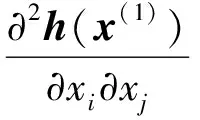
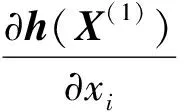
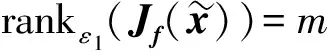
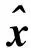
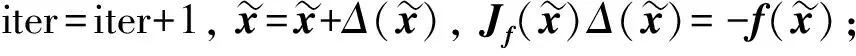
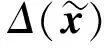
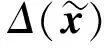
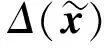

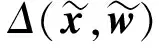
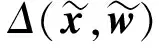
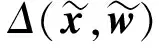
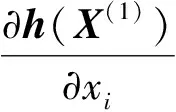
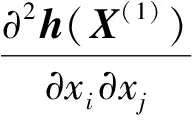
3 数值算例