开关频率对SPWM逆变器动态行为的影响
张金科,伍小杰,赵明龙,王 钊
(中国矿业大学 信息与电气工程学院,江苏 徐州 221008)
0 引言
近年来,电力电子学在工业、航天、能源和家居等领域取得了蓬勃的发展。在中高压大功率逆变器中,开关器件常工作在较低的开关频率以减少损耗并提高变频器出力,但这会造成电流剧烈畸变、谐波增大甚至出现失稳以致变频器不能工作等严重问题。为什么开关频率降低会带来上述影响就成了一个很重要的研究课题,已有学者从变频器建模的角度进行了深入的研究[1],本文则主要从混沌的角度来尝试分析上述问题。
混沌是一门研究确定论系统内在随机性的科学[2],在过去二十多年里已有众多学者将它应用在电力电子变换器的研究中[3-5],并形成一套有效的研究方法,如对变换器建立基于开关周期的离散模型和雅可比矩阵特征值判断稳定性等[6-9]。与电力变换器的拓扑结构相对应,变换器模型的实质是一组非线性微分方程的叠加,因此在建模时常把变换器与被控对象组成的系统看作分段光滑的非线性动力系统。文献[4]研究了DC-DC变换器中的混沌现象,建立了实用的迭代离散模型,但对工作在正弦逆变状态的正弦脉宽调制(SPWM)逆变器讨论较少;文献[10]系统地研究了单相SPWM在主电路及控制器参数变化时的混沌分岔现象,在文献[4]迭代离散模型的基础上建立了新的离散数学模型,并针对正弦逆变的情况讨论了参数变化对系统稳定性的影响,但未涉及开关频率方面的研究;文献[11]研究了H桥直流斩波电路中的边界碰撞分岔现象;文献[12]研究了DC-DC变换器中的混沌现象,并总结了混沌研究中常用的建模方法。
当前电力电子中的混沌研究主要集中在数学建模、参数变化分析等方面,对系统稳定性影响的讨论多是围绕控制器系数、直流侧电压、阻感负载参数等方面,开关频率对系统产生的分岔混沌现象还鲜有研究。本文尝试从开关频率对逆变器的影响切题,系统地研究了由不同开关频率造成的分岔现象,对电流时域解中的开关频率指数项进行了合理的简化,得出了使系统稳定的参数域图,并和仿真得出的二维分岔图进行了对比分析。本文以H桥为研究对象,讨论了电流脉宽调制中的混沌现象,对深入研究低开关频率下的非线性现象研究有指导意义。
1 单相SPWM逆变器精确离散模型
图1是SPWM的H桥逆变器电路图。

图1 单相SPWM逆变器电路图Fig.1 Circuit diagram of single-phase SPWM inverter
单相SPWM逆变器存在2种工作状态:状态1为VT1和 VT3开通,VT2和 VT4关断;状态 2为 VT2和 VT4开通,VT1和VT3关断。相应的状态方程分别如式(1)和(2)所示。
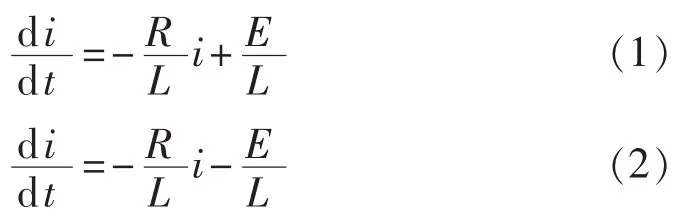
假设状态1的工作时间为tn,并定义占空比dn=tn/Ts,则状态 2 的工作时间为(1-dn)Ts,其中 Ts为控制器的时钟周期,fs=1/Ts即为逆变器的开关频率。
频闪采样法是一种以时钟周期Ts为采样间隔的建模方法,它忽略单个采样周期内系统状态的变化,而只关注采样点时刻的系统状态,其基本原理是使用第nTs时刻的状态来表示第(n+1)Ts时刻的状态。设nTs时刻的电感电流为in,连续求解微分方程(1)和(2)可得第(n+1)Ts时刻的电流为:

当采用比例控制时,占空比dn作如下取值:

其中,k为比例系数;Iref为给定电流量。
2 分岔、混沌现象观察及分析
对于离散映射式(3),通过改变Ts来研究开关频率对系统稳定性的影响。逆变器仿真参数为:E=100 V,R=10 Ω,L=10 mH,Iref=5sin(40πt)A,即 α=10 A,τ=0.001 s,f1=20 Hz。其中,f1为给定信号Iref的频率。
2.1 稳定状态
取比例控制系数k=0.8,当开关频率fs=5kHz时,系统处于稳定状态,取每个nTs时刻的电流采样点绘成频闪采样图,如图2(a)所示。图2(b)是把每个采样电流点连接起来的直线,它近似反映了采样周期为Ts的时域波形,该图描述了两相邻采样点电流的变化情况。稳定状态又称周期一状态,频闪采样电流的频谱分析如图2(c)所示。

图2 系统在周期一状态下的行为Fig.2 System behavior during period 1
2.2 周期二状态
当开关频率fs=3.8 kHz时,系统处于周期二状态,即分岔状态。此时的电流频闪采样图为2条正弦线,如图3(a)所示。电流时域图3(b)显示了电流在2条正弦线之间的波动情况。从频谱分析图3(c)中可以看出,在周期二状态,电流开始出现高次谐波,THD值也明显大于周期一。

图3 系统在周期二状态下的行为Fig.3 System behavior during period 2
2.3 混沌状态
当开关频率fs=2.6 kHz时,系统已经处于混沌状态,从频闪采样图来看,此时正弦波不再有明显的规律可循,每个波峰处的峰值近乎随机。频谱分析表明,电流的高次谐波大幅增加,THD也比周期二更高。
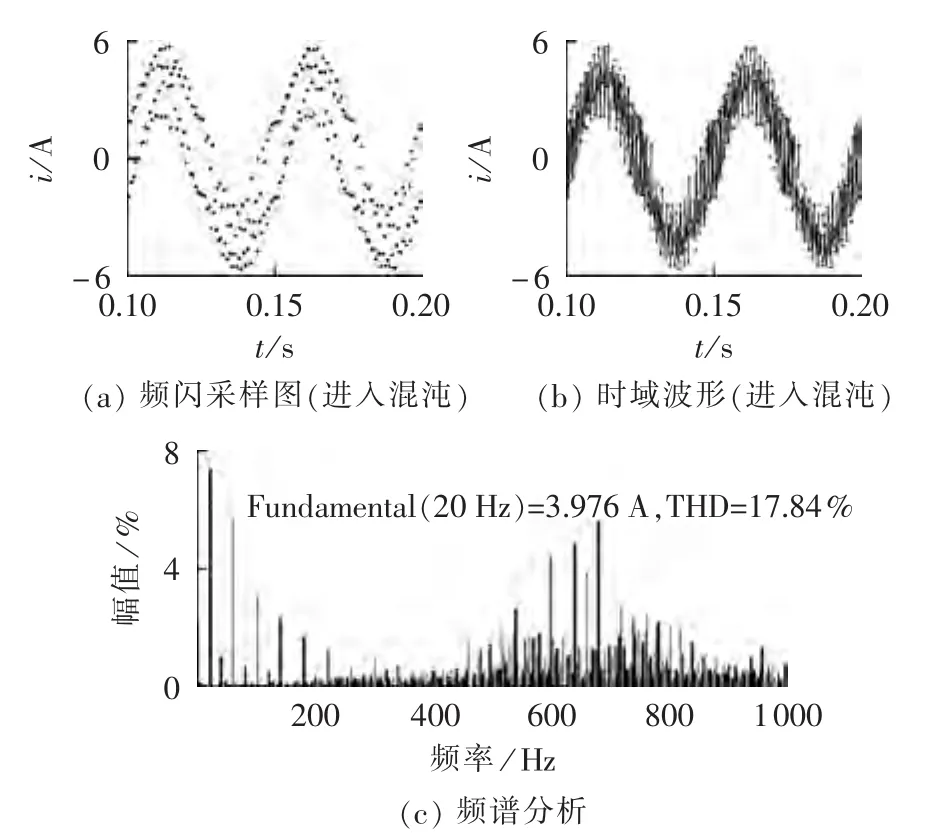
图4 系统在混沌状态下的行为Fig.4 System behavior during chaos
2.4 分岔图与稳定性分析
分岔图是研究混沌的常用方法,它能清楚地表明参数变化对系统稳定的影响,仅考虑1个变量的分岔图称为一维分岔图,考虑2个变量对系统影响的分岔图称为二维分岔图[13-14]。
对于给定电流信号 Iref=5sin(40πt)A,在其波峰时刻对电感电流进行采样,绘制出不同开关频率下的采样点,即得电流随开关频率变化的一维分岔图,如图5所示。在开关频率fs>4 kHz时,系统稳定,处于周期一状态;在开关频率fs<4 kHz时,系统不再稳定,采样电流开始分岔,系统处于周期二状态;随着开关频率继续降低,系统进入混沌状态,采样电流不再遵循明显的规律,从图5看出,采样频率在2 kHz左右时系统的无序性最为明显。当开关频率fs降至1 kHz以下,H桥逆变器已没有逆变效果,其输出是周期与开关频率相等的方波,采样电流逐渐趋近2个固定的值。

图5 比例控制下的一维分岔图(k=0.8)Fig.5 1-D bifurcation diagram with proportional controller(k=0.8)
在实际工程中,总希望逆变器工作在周期一状态。为得到使系统稳定运行的参数域,可通过求解离散映射在不动点处的导数来分析周期运动的稳定性。对于式(3)所示的离散映射,令in=in+1,有:

求解式(5)中的未知量in即得系统稳定运行在周期一状态下的不动点,用i*表示。
对式(3)求导,并根据 Floquet理论[15]定义特征乘子

则有:

为求得参数Ts与k对系统稳定的影响,又因为系统稳定时不动点i*≈Iref,在不考虑给定量Iref影响的前提下,故可令式(7)中的in=Iref,因此简化后的特征乘子为:




由式(10)可以看出,比例系数k与开关频率fs近似成线性关系,满足式(10)的k与fs所构成的区域称为系统的稳定域,如图6所示。
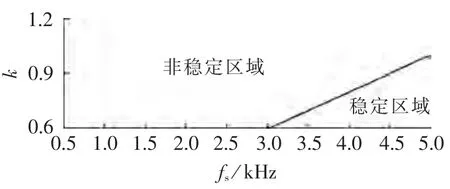
图6 相空间k-Ts里的稳定域Fig.6 Stability zone in k-Tsspace
通过仿真给出了比例控制下的二维分岔图,如图7所示。图中黑色区域表示稳定,白色区域表示混沌,可以看到周期一状态位于右下角黑色三角区域,这与上述计算得出的稳定域是一致的。

图7 相空间k-Ts上的二维分岔图Fig.7 2-D bifurcation diagram in k-Tsspace
3 时滞反馈控制低频混沌
3.1 控制器设计
时滞反馈控制器TDFC(Time-Delayed Feedback Controller)在比例控制器的基础上增加了滞后环节,其目的是增强周期轨道的稳定性,滞后时间常数一般选为离散采样的周期[16-19]。时滞反馈控制器结构如图8所示,控制信号γn由比例信号γPn和时滞信号γDn组成,其中 γPn=k(Iref-in),γDn=η(in-in-1),其中 k、η分别为比例系数和时滞系数。
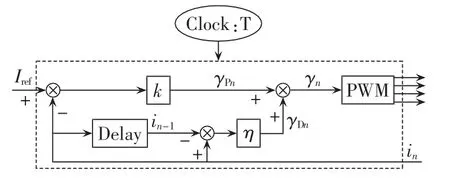
图8 时滞反馈控制器结构Fig.8 Structure of TDFC
采用时滞反馈控制时,占空比dn取值如下:

3.2 控制效果
改变时滞控制器的时滞系数,观察电感电流的稳定性。当k=0.8、η=0.1时,电流随开关频率变化的分岔图如图9所示。与图5相比较,比例控制系统在开关频率fs<4 kHz时便已脱离稳定状态,而加入TDFC控制的系统在开关频率fs<3 kHz时才开始变得不稳定,这说明TDFC可有效增强系统在中低频段的稳定性。图10展示了时滞系数η=0.1时相空间k-Ts上的二维分岔情况,与图7相比,可以看出右下角黑色三角形稳定域的范围大幅增加了。

图9 TDFC控制下的一维分岔图(η=0.1)Fig.9 1-D bifurcation diagram with TDFC(η=0.1)

图10 TDFC控制下的二维分岔图(η=0.1)Fig.10 2-D bifurcation diagram with TDFC(η=0.1)
当k=0.8、η=0.2时,电感电流的一维分岔图如图11所示,当开关频率fs<2 kHz时,系统才开始进入不稳定状态。相空间k-Ts上的二维分岔图如图12所示,与图10相比,可以看出当时滞系数η=0.2时,系统在k-Ts相空间右下的大片区域都能保持稳定。仿真表明,在当前电路参数下,控制器参数取k=0.65、η=0.2时,系统的开关频率在1.5 kHz时开始出现不稳定现象。

图11 TDFC控制下的一维分岔图(η=0.2)Fig.11 1-D bifurcation diagram with TDFC(η=0.2)

图12 TDFC控制下的二维分岔图(η=0.2)Fig.12 2-D bifurcation diagram with TDFC(η=0.2)
3.3 稳定边界计算
加入时滞控制后,系统出现2个变量即in和in-1,故由式(3)和式(11)定义的离散映射是一个二阶系统。重新定义系统状态变量xn=in-1-i*,yn=in-i*,则有如下二阶电流离散模型:

结合式(3)、(11)、(12),消去变量 in+1,可得系统离散状态方程:

如图13所示,在电感电流稳定时占空比是不饱和的,其时域波形是一条平滑的曲线;当电感电流处于分岔状态或混沌状态,占空比就会出现饱和的情况。所以在稳定参数域内,只需要考虑dn不饱和的情况,即:


图13 不同开关频率下的电感电流波形图Fig.13 Waveforms of inductor current for different switching frequencies
结合式(14),求式(13)雅可比矩阵有:
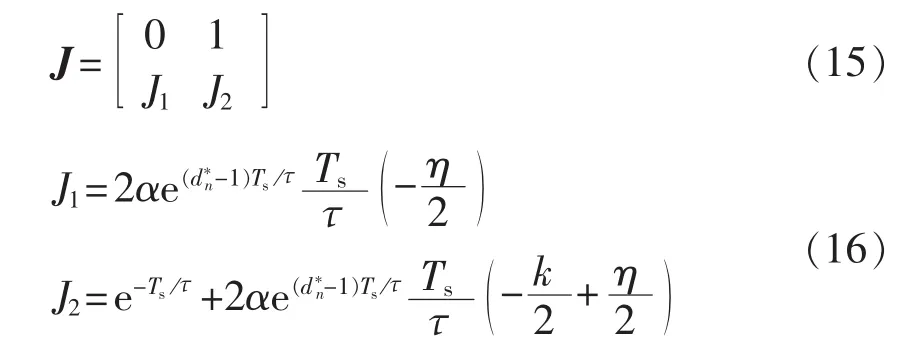
根据Floquet理论,为使系统保持稳定,需满足特征乘子,其中λ是雅可比矩阵J的特征值。令可得如下特征方程:

使用朱利判据[4]来计算相空间η-Ts上的稳定域,需要满足下述条件:


结合式(18)、(19),可得出 η-Ts的关系满足如下不等式:

需要注意的是,不动点i*是与开关频率fs有关的函数,但仿真表明开关频率对i*的影响很小,当fs=3.5 kHz、k=0.8时,i*=4.383,此时对应的占空比 dn*=0.7468。在对稳定域精度要求不高的情况下,不动点i*与占空比dn*取上述恒定值是合理的。
式(20)描述的区域如图14所示,它是一个近似三角形的稳定域;在交点处,当η约取0.22时,开关频率fs可取到最小值约2.0 kHz,这表明在比例系数k=0.8时,时滞控制器的最优效果可使开关频率降至2 kHz。相空间η-Ts上的二维分岔图如图15所示,可以看出仿真得出的稳定边界同上述计算是基本一致的。

图14 相空间η-Ts上的稳定域(k=0.8)Fig.14 Stability zone in η-Tsspace(k=0.8)

图15 相空间η-Ts上的二维分岔图(k=0.8)Fig.15 2-D bifurcation diagramin η-Tsspace(k=0.8)
3.4 PI调节器的稳定域求解
在使用PI控制器对电流环进行调节时,系统的阶次会增加,本文通过联立控制器和被控对象的整体模型,并求其雅可比矩阵的特征值来计算系统的稳定区间。
PI控制器的传递函数为:

采用后项差分法,对式(21)进行离散化,可得PI控制器的离散方程,即:

则PI输出控制信号可表示为:

定义新的状态变量为 xn=γn-1、yn=in-1、zn=in,则有如下状态方程:

易求得式(24)的雅可比矩阵为:


则通过求式(25)的特征值即可解出系统的稳定域,本文采用MATLAB编程给出式(25)特征值的数值解,如图16所示。

图16 开关频率变化时的根轨迹图(Kp=0.6,Ki=0)Fig.16 Eigenvalue locus when switching frequency changes(Kp=0.6,Ki=0)
图16显示了开关频率fs变化时系统的根轨迹图,其中控制器的参数为Kp=0.6、Ki=0,这也是与图6中的结果是互为验证的。开关频率fs在3.1 kHz处从坐标(-1,0)处越过单位圆,则可知此时发生的是倍周期分岔。
图17给出了系统在相空间Ki-Kp-fs下的稳定区间,该图更直观地显示了PI控制器的参数在不同开关频率下的取值范围。

图17 系统在相空间Ki-Kp-fs下的稳定域图Fig.17 Stability zone in Ki-Kp-fsspace
4 仿真与实验验证
4.1 仿真验证
针对式(3)、(11)所定义的离散系统,分别在开关频率为3 kHz和2 kHz时进行仿真,仿真结果如图18所示。在k=0.8、fs=3 kHz时,采用比例控制的H桥逆变器工作在分岔状态;在t=0.75 s时刻加入时滞环节,系统从分岔状态过渡到周期一状态,电感电流呈稳定的正弦波,如图18(a)所示。当开关频率fs=2 kHz时,采用比例控制的H桥逆变器工作在混沌状态,电流波形紊乱呈随机状态;在t=0.75 s时刻加入时滞环节,当时滞系数η=0.22时,控制效果最好,系统从混沌状态过渡到周期一状态,电感电流输出正弦且保持在稳定状态,如图18(b)所示。

图18 仿真结果Fig.18 Simulative results
4.2 实验验证
搭建如图1所示的H桥逆变器实验平台,主电路的参数如下:E=100 V,R=10 Ω,L=10 mH,Iref=5 sin(40πt)A;控制器采用 dSPACE1104 实验平台,系统采样频率为20 kHz;观察单相SPWM逆变器在不同开关频率下的分岔混沌情况,并使用TDFC进行控制,实验结果如图19所示。
图19(a)、(b)展示了逆变器运行在稳定状态的情况,电感电流的频闪采样图是一条规则的正弦线;当开关频率降为fs=2.5 kHz时,系统处于倍周期分岔的临界点,在时间t=3.02 s加入TDFC控制后,电感电流过渡到周期一状态,电流频闪采样图如19(c)所示;当开关频率降为fs=2 kHz时,电感电流时域波形如图19(d)所示,系统处于周期二状态,加入TDFC控制后,电感电流从分岔状态过渡到周期一状态并保持稳定,其频闪采样图分别为图19(e)、(f)所示。

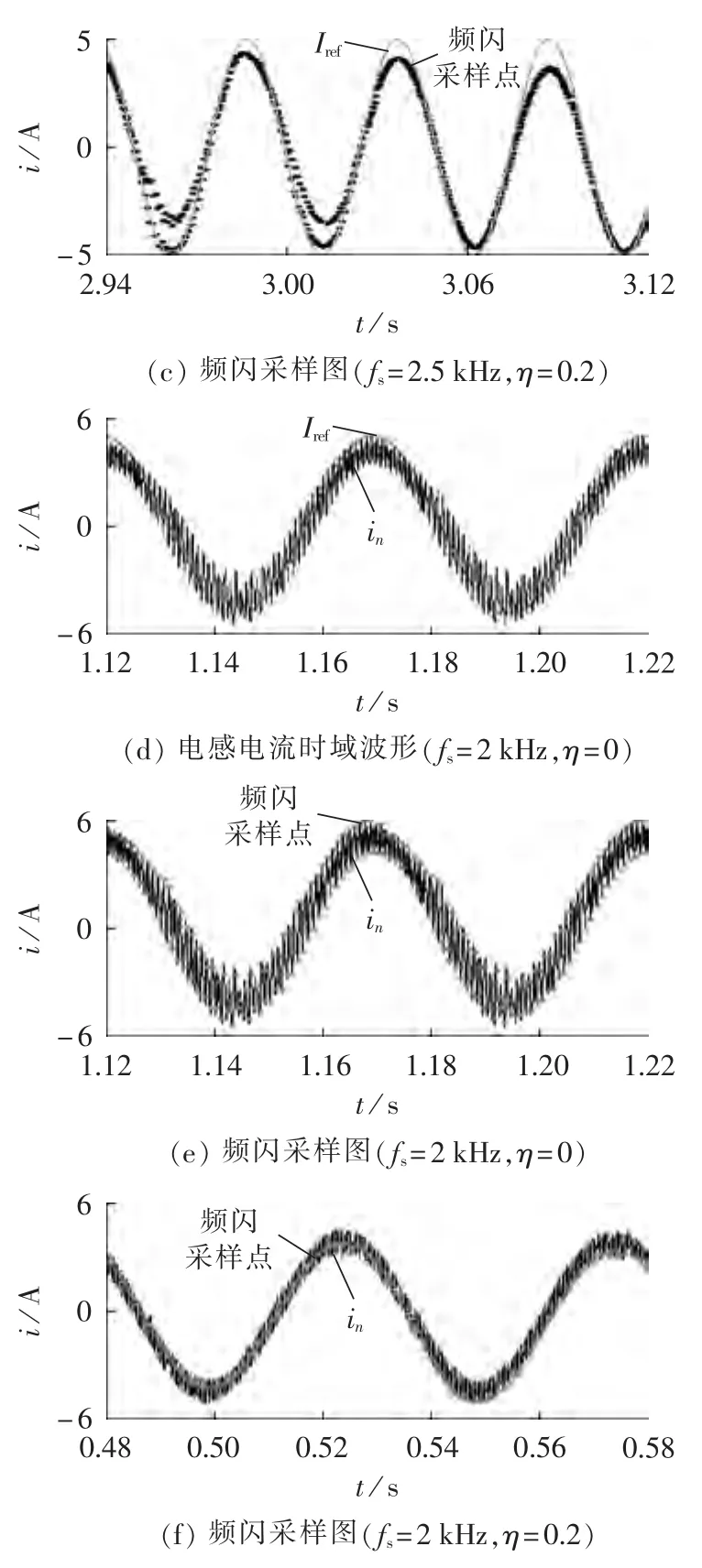
图19 实验结果Fig.19 Experimental results
5 结论
本文主要研究了开关频率对单相SPWM逆变器动态行为的影响,做了以下三方面的工作:第一,采用比例控制下的H桥一阶离散模型,在k-Ts相空间内对系统进行了稳定性分析;第二,使用TDFC抑制了系统在中低频段的混沌状态,建立了时滞反馈控制下的H桥二阶离散模型,并给出了相空间η-Ts上的二维分岔图;第三,研究了PI控制器在不同开关频率下的稳定条件,通过计算雅可比矩阵的特征值给出了系统稳定运行的参数域。
研究开关频率造成的混沌对逆变器的设计具有重要指导意义,本文所采用的TDFC可有效消除H桥中因开关频率降低带来的混沌;对于其他类型的逆变器,可以根据不同的拓扑建立相应的离散模型,本文的分析和控制方法具有一定的普适性。

