障碍期权定价的混合Laplace—Adomian方法探讨

李晓敏

【摘要】 期权是一种重要的金融衍生工具，价格作为期权最核心的部分得到人们极大的关注。其中最著名的是布莱克与斯科尔斯在20世纪70年代提出的Black-Scholes公式，许多学者将该公式运用于不同种类的期权计价中，并且在具体求解过程中试用了大量不同思路的数学方法。本文沿着这一思路，将双障碍期权抽离出来，研究它价格的计算方法，具体做法为将Laplace变换与Adomiam分解方法结合，希望能得到计算更为简洁的求解模型。

【关键词】 期权 布莱克-斯科尔斯公式 拉普拉斯变换 Adomian分解

一、背景介绍

1、期权定义

期权是指在特定时间内以特定价格买卖一定数量交易品种的权利。合约买入者或持有者以支付期权费的方式拥有权利；合约卖出者或立权者收取期权费，在买入者希望行使权利时，必须履行义务。由于对期权的拥有者而言，它代表的是一项权利而不是义务，因此在金融市场中它是有一定价值的金融工具，而又由于期权是在它所对应的标的资产基础上衍生而来的，因此它被称作为金融衍生工具。

2、期权价值

期权的价值是研究期权问题的核心，它主要由内涵价值和时间价值两部分组成。内含价值又称履约價值，指期权本身所具有的价值，也是期权履行合约时所能获取的利润。它反映了期权的敲定价格与标的资产市场价格之间的变动关系。时间价值是指期权买方随着时间的延续及相关商品的价格波动可能使期权增值时，买入这一期权所付出的权利金金额。期权时间价值的变化规律为：随着期权合约剩余有效期的缩短而减小。因为对权力买方而言，市场发生有利变化的可能性越大，获利的机会也就越多，他愿意支付的时间价值也就越高；从期权卖方而言，有效期越长，他需履行义务的时间也就越长，因此承担的风险较大，收取的时间价值也就较高。影响期权价格的因素主要有以下几点。

（1）与标的资产有关的因素。标的资产的当前价值。由于看涨期权规定了由固定价格购买标的资产的权利，因此标的资产当前价格的上升能增加看涨期权的价值；看跌期权则恰好相反。

标的资产价格变化的方差。到期日内标的资产价格的波动性，对看涨看跌期权一样，在其他因素不变的情况下，标的资产价格变化的幅度越大，期权的价值越高。因为期权买方的损失最大不会超过所支付的期权费，但却会从标的资产价格的剧烈变化中获取巨大收益。

标的资产支付的红利。标的资产支付现金红利会影响标的资产的价值，从而进一步影响期权的价值。

（2）与期权合约相关的因素。期权的执行价格。期权的执行价格在期权的到期日之内是固定的。对看涨期权而言，由于合约规定了由固定价格购买标的资产的权利，期权的价值随执行价格的上升而下降。如股票以100元的价格交易，执行价格是80元的看涨期权内在价值为20元，而执行价格为90元的看涨期权的内在价值为10元。

期权的到期期限。无论是看涨期权还是看跌期权，在其他因素都一定的情况下，期权的价值都会随到期日的临近而减小。

与金融市场相关的因素。主要是无风险利率的影响，利率升高会使得看涨期权的价值增加，而使看跌期权的价值减小。

3、期权计价模型

期权定价是指期权价格的确定，期权的价格为期权买方为获得期权合约所赋予的权利而向卖方所支付的费用。在期权的交易中，它有很重要的意义，同时也是十分复杂的。

1973年，美国的Fisher Black和Myron S.Scholes联合发表了题为“期权和公司债务的定价”的文章，该文章被刊登在《政治经济学》杂志上。文中提出了Black-Scholes公式用来计算欧式看涨期权的定价问题。公式的最终表达式为：

其中，C代表期权价格，它是关于股票价格s和时间？子的函数，？滓指股票价格的波动性，rf代表无风险利率。

尽管B-S模型的提出具有重要的意义，但是它也并不是完美的。因此，它并没有终止人们对期权定价领域的研究，而是为更进一步的研究奠定了基础。在此之后的40多年来，主要出现了如下重要的成果：Merton（1973）考虑了股利和随机利率模型；Brennan（1978）阐述了跳跃过程模型；Macbeth和Merville（1980）检验了B-S模型；Leland（1985）、Dokuchaev（1998）和Lionel Martellini（2000）将交易成本纳入考虑之中；P.P.Boyle（1998，1999）对多变量或有衍生物进行了求解；Vasicek（1997）、Cox Ingersoll和Ross（1985）、Ho和Lee（1986）研究了短期利率模型；Scott（1987）、Steeley（1997）、Finance和Tomas（1997）、Nandi（1999）、Zran和Forsyth（1998）、Danielsson（1998）、Duan（2001）研究了随机波动率问题；Chang（2001）研究了随机利率问题；Ball和Torous（1983）、Black 和Karasinski（1991）、Jamashidian（1989）、Das（1997）、Ho和Stapleton（1997）探讨了债券期权；Garman和Kohlhagen（1983）、Amin和Jarrow（1991）研究了货币期权；Campbell和Whaley（1992）研究了指数期权；Wall和Pringle（1989）、Hagn和Bazley（1997）、Hubner（2001）研究了利率互换问题；Rubinstein（1979，1994）对二叉树方法进行了系统阐述；P.P.Boyle （1994）对障碍期权的求解进行了研究；P.P.Boyle（1999）对服从CEV的回望期权和障碍期权进行了系统研究；J.Hull A.White（1990，1993，1994）对股票期权及利率期权进行了大量阐述；D.Heath R.Jarrow（1990，1992）和Black（1995）也对利率期权定价问题进行了阐述；另外，Boris（1998，2002）等对仿射期限结构问题进行了研究。在完全金融市场的环境下，期权定价方法除了B-S模型之外，还有二叉树模型、蒙特卡罗模型及有限差分法等。

4、本文内容

障碍期权作为众多期权中的一种，由于其价格比普通期权要便宜得多，因此在市场上交易十分活跃。障碍期权的价值不仅取决于标的资产到期日的价格，还取决于标的资产的价格在到期日之前是否会超过合同所限定的“障碍”，这也为期权价值的确定带来了阻碍。已有的计算障碍期权的方法往往要消耗大量的计算时间，本文试图将Laplace变换同Adomian分解法结合，希望得出计算障碍期权价格的更有效的算法。本文的主要内容包括：第一，介绍期权的基本含义，主要类型；第二，简单介绍Black-Scholes公式及期权定价方面的研究现状；第三，重点将奇异期权中的双障碍期权提出来，计算它的价格，主要思路为先将Black-Scholes公式中的偏微分方程经过Laplace变换，再将变换后的方程用Adomian分解法进行求解，最后再经Laplace逆变换求出我们所要的方程解；第四，对障碍期权定价的混合Laplace-Adomian方法的优劣进行分析，并加以总结。

二、模型

在此部分我们以双障碍看涨期权为例，探讨混合Laplace-Adomian方法的具体步骤。

首先从Black-Scholes公式开始：

其中，C代表期权价格，它是关于股票价格s和时间？子的函数，？滓指股票价格的波动性，rf代表无风险利率，Cs是指期权价格C对股票价格的一阶偏导，Css是期权价格对股票价格的二阶偏导，C？子是期权价格对时间的一阶倒数。

边界条件和起始条件如下：

为了进行下面的步骤，我们把经过Laplace变换后的式（6）先放一放，先来讨论Adomian分解方法在解常微分方程中的应用。

已知待定求解方程形式为：

边界条件为：

运用Adomian方法得到：

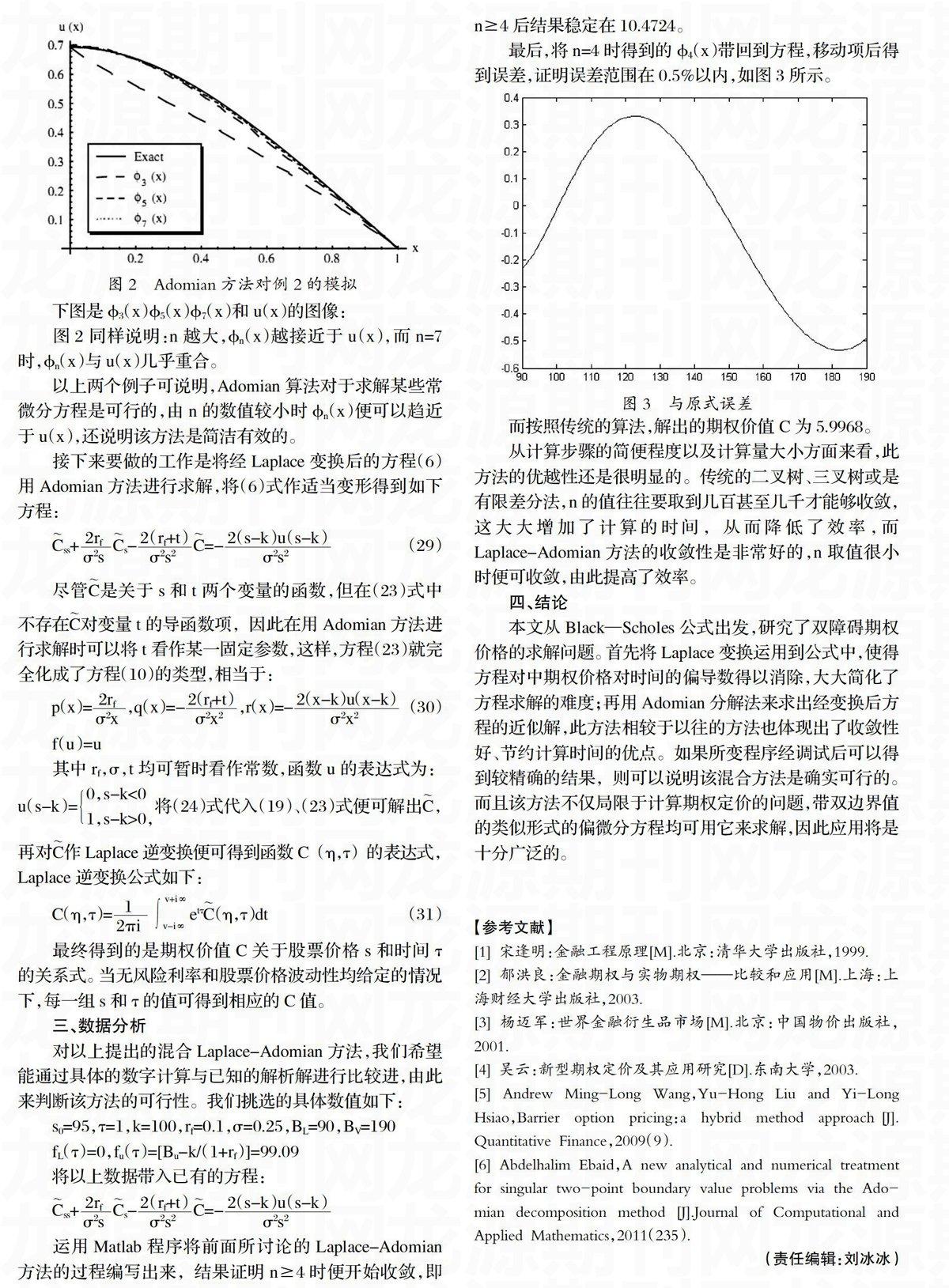
图2同样说明：n越大，？准n（x）越接近于u（x），而n=7时，？准n（x）与u（x）几乎重合。

以上两个例子可说明，Adomian算法对于求解某些常微分方程是可行的，由n的数值较小时？准n（x）便可以趋近于u（x），还说明该方法是简洁有效的。

接下来要做的工作是将经Laplace变换后的方程（6）用Adomian方法进行求解，将（6）式作适当变形得到如下方程：

最终得到的是期权价值C关于股票价格s和时间？子的关系式。当无风险利率和股票价格波动性均给定的情况下，每一组s和？子的值可得到相应的C值。

三、数据分析

对以上提出的混合Laplace-Adomian方法，我们希望能通过具体的数字计算与已知的解析解进行比较进，由此来判断该方法的可行性。我们挑选的具体数值如下：

运用Matlab程序将前面所讨论的Laplace-Adomian方法的过程编写出来，结果证明n？叟4时便开始收敛，即 n？叟4后结果稳定在10.4724。

最后，将n=4时得到的？准4（x）带回到方程，移动项后得到误差，证明误差范围在0.5%以内，如图3所示。

而按照传统的算法，解出的期权价值C为5.9968。

从计算步骤的简便程度以及计算量大小方面来看，此方法的优越性还是很明显的。传统的二叉树、三叉树或是有限差分法，n的值往往要取到几百甚至几千才能够收敛，这大大增加了计算的时间，从而降低了效率，而Laplace-Adomian方法的收敛性是非常好的，n取值很小时便可收敛，由此提高了效率。

四、结论

本文从Black—Scholes公式出发，研究了双障碍期权价格的求解问题。首先将Laplace变换运用到公式中，使得方程对中期权价格对时间的偏导数得以消除，大大简化了方程求解的难度；再用Adomian分解法来求出经变换后方程的近似解，此方法相较于以往的方法也体现出了收敛性好、节约计算时间的优点。如果所变程序经调试后可以得到较精确的结果，则可以说明该混合方法是确实可行的。而且该方法不仅局限于计算期权定价的问题，带双边界值的类似形式的偏微分方程均可用它来求解，因此应用将是十分广泛的。

【参考文献】

[1] 宋逢明：金融工程原理[M].北京：清华大学出版社，1999.

[2] 郁洪良：金融期权与实物期权——比较和应用[M].上海：上海财经大学出版社，2003.

[3] 杨迈军：世界金融衍生品市场[M].北京：中国物价出版社，2001.

[4] 吴云：新型期权定价及其应用研究[D].东南大学，2003.

[5] Andrew Ming-Long Wang，Yu-Hong Liu and Yi-Long Hsiao，Barrier option pricing：a hybrid method approach[J].Quantitative Finance，2009（9）.

[6] Abdelhalim Ebaid，A new analytical and numerical treatment for singular two-point boundary value problems via the Adomian decomposition method[J].Journal of Computational and Applied Mathematics，2011（235）.

（責任编辑：刘冰冰）