横向同性分层介质三维电磁模拟的高阶DTA算法

陈桂波，张烨，潘轶群

（1.长春理工大学 理学院，长春 130022；2.长春市农业机械研究院，长春 130062）

矩量法是进行电磁场三维数值模拟的一种常用而有效的方法，在农业遥感、探地雷达、资源勘探等领域具有十分广泛的应用［1，2］。该方法首先建立一个关于散射体内电场或电流分布的第二类弗雷德霍姆积分方程，然后将积分方程离散形成一个矩阵方程，求解该矩阵方程可以得到散射体内的电场分布，进而得到空间任意位置的电磁场分布［3］。

由于矩量法一般只针对有限大小的散射体进行离散，因此与需要全空间离散的有限差分与有限元法相比，矩量法具有离散数目少、求解精度高等优点。但该方法在使用过程中也存在一个不容忽视的问题，由于积分方程的离散化系数矩阵为复数致密矩阵，存储和计算该矩阵需要大量的计算机内存和计算时间，致使矩量法在实际应用中往往受到较大的限制。为了克服这个问题，一些学者提出了积分方程的近似解法，可达到满意的计算精度并且具有占用内存少、计算效率高等固有优点，在近年来逐渐发展成为计算电磁学领域中的一个研究热点。其中由量子力学理论发展而来的Born近似是最常见的一种近似方法［4］，该方法虽然形式简单、易于编程，但使用条件极为苛刻，往往要求其有频率较低以及散射体尺寸较小等弱散射条件。Habashy等人在Born近似的基础上提出了扩展Born近似算法［5］，该方法通过引入散射张量将散射体内电场与入射电场联系起来，其计算精度和适用范围都要优于Born近似，但该方法存在一个明显不足就是当散射体距发射源较近以及散射体内电场分布极不均匀时计算精度较差；Zhdanov等人分别提出了QL和QA近似［6，7］，并进一步给出了相应的高阶级数展开形式；Song等人基于局部非线性近似原理提出了一种依赖于入射源的对角张量近似（DTA）算法［8］，数值实例证明该方法相对于前几种方法具有更高的计算精度和更广泛的适用性，并且已经成功用于层状介质的三维反演成像［9］。但是，上述几种方法的应用目前还都只局限于各向同性介质，而关于各向异性介质条件下相应的近似算法研究却鲜有报道。各向异性介质的电磁模拟与特性分析是在实际中经常会遇到的问题，因此本文将相对较新、性能较好的DTA算法推广应用到各向异性分层介质（为简单起见，本文只考虑横向同性分层介质），为进一步提高DTA求解积分方程的计算精度，本文提出一种满足压缩映射条件的高阶DTA级数算法。

文中首先给出求解积分方程的DTA算法基本原理，然后基于压缩算子理论得到一种总是收敛的高阶DTA级数解，最后通过数值实例对比检验了本文算法的有效性。

1 DTA近似基本原理

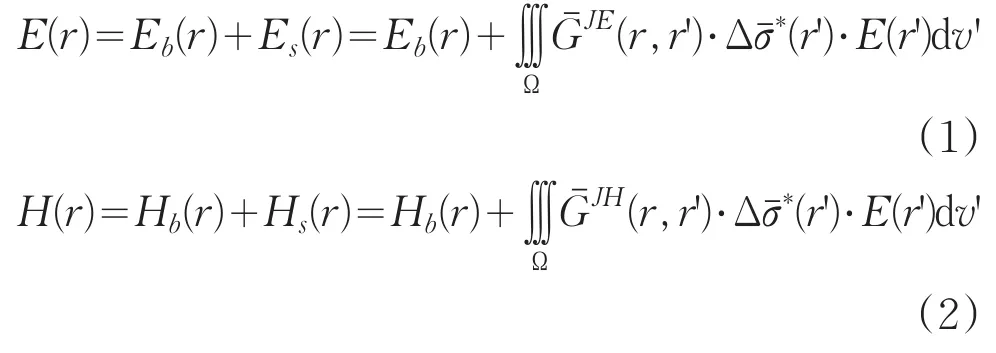
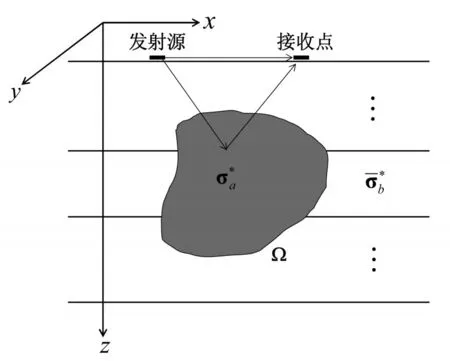
图1 三维模型示意图

DTA算法用于求解积分方程的基本原理是引入一个与入射源有关的对角张量将散射体内的散射电场与入射电场联系起来，即：

其中 Γ=diag(γx,γy,γz)为对角张量，其各个元素表达式可利用文献［8］中的局部非线性近似方法来得到：

这里Ebξ为入射电场Eb的ξ分量，而EBξ为矢量

的ξ分量。利用式（3），可将散射体内的电场写为：

再由方程（1）和（2）就可以得到空间任意位置的电磁场。

2 高阶DTA级数

方程（1）也可以写成算子方程的形式：

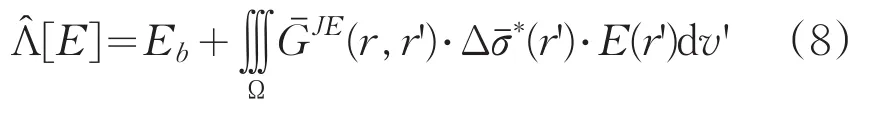
根据积分方程理论，方程（7）的解可由迭代法得到：

由上式容易看出，若E(0)=Eb，则E(1)即为传统Born近似解，k＞1时方程（1）的解可以展开成高阶Born级数的形式；若，则 E(1)为DTA解，同理在这种情况下k＞1时方程（1）的解也可以展开成高阶级数的形式，称之为高阶DTA级数。根据算子理论可知，应用迭代法求解方程（7）只有在A为压缩算子，也就是的L2范数小于1的条件下才是收敛的。遗憾的是，算子A只有在散射体尺寸较小以及电导率差异较小等弱散射条件下才是压缩算子。为了克服这个问题，利用文献［11］中介绍的线性变换方法，在方程（1）两端同时左乘一个对角张量，可以得到关于参量E的算子方程：

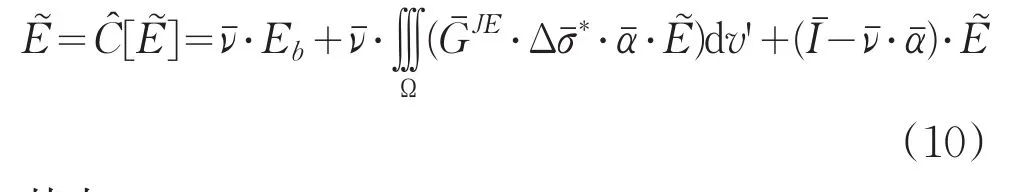
其中

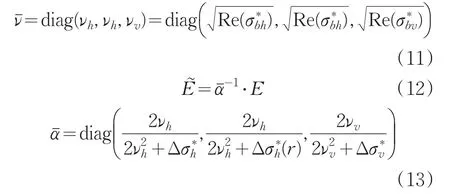
由文献［3］可知，算子 C是 L2(Ω)上的压缩算子，也就是说算子方程（10）满足压缩映射条件，进而应用迭代法将方程（10）的解展开成高阶级数对于任意电导率分布等参数条件下总是收敛的。为了验证这一点，考虑具有图2所示结构的三层横向同性介质模型，中间层厚度为20m，其余两层均为半空间。在图示直角坐标系中，大小为30m×120m×90m的散射体位于第三层介质中，其中心坐标为（0，0，75）。假定第一层介质为空气，第二层介质的横向和纵向电导率分别为0.1S/m和0.02S/m，第三层介质的横向和纵向电导率分别为0.01S/m和0.005S/m。在（－10m，0，0）处有一个沿x方向单位大小的电偶极子，发射频率为1000Hz，接收点位于（10m，0，0）。分别采用基于方程（7）的传统迭代法和基于方程（10）的压缩迭代法计算了散射电场x分量的相对误差（这里表示应用严格矩量法的计算结果［3］），图3（a）～（c）给出了散射体的电导率为0.1S/m、0.05S/m、0.0005S/m时两种方法计算的相对误差随迭代次数的变化曲线。可以看出，传统迭代法的计算结果均不收敛，尤其是在散射体电导率大于分层介质电导率时，散射体电导率越高，发散则越严重，而压缩迭代法在三种情况下的计算结果都是收敛的，可见本文引入的压缩算子对于各种情况下积分方程迭代收敛性能的提高作用是非常明显的。

图2 三层横向同性介质模型

3 数值计算结果

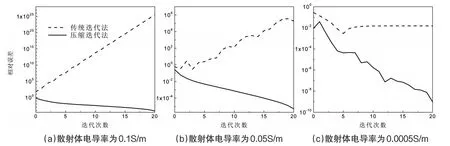
图3 传统迭代法与压缩迭代法的相对误差

考虑一个与图2具有相同几何参数的三层介质模型，并且依旧假定第一层介质为空气，而第二层和第三层介质的横向电导率分别为0.1S/m和0.01S/m，纵向电导率分别为0.02S/m和0.005S/m。单位大小的垂直磁偶极子可沿x轴任意移动，接收点也位于x轴上，发射源与收收点之间的距离为150m，并且选择发射源与接收点的中心作为记录点，发射频率为1000Hz。分别采用传统Born近似、DTA近似、本文的高阶DTA级数方法以及严格矩量法［3］计算了散射磁场的垂直分量分布，图4和图5分别给出了当散射体电导率为0.1S/m和0.001S/m时的计算结果。从图4中曲线可以看出，本文的高阶DTA级数法收敛速度较快，3阶展开就几乎可以达到精确结果，并且DTA近似（0阶DTA级数）的计算精度要高于传统Born近似。从计算效率来看，在同一台计算机上，严格矩量法计算图中31个节点需要3分钟左右，而3阶DTA近似则小于1分钟，可见本文算法在保证计算精度的同时可使积分方程的求解效率得到有效提高。

观察图5曲线可以发现，几种方法计算结果之间的差别没有图4曲线那样明显，这是由于当散射体电导率为0.001S/m时电导率差异相对于分层介质的电导率来说较小，产生的散射较弱，导致散射体内入射场在总场中所占有的比例较大，因此各种方法的近似程度均比目标体电导率为0.1S/m时要高。在实际计算中，可以根据散射体的性质来选择较少阶数的DTA展开，以便在保证计算精度的同时进一步提高计算速度。

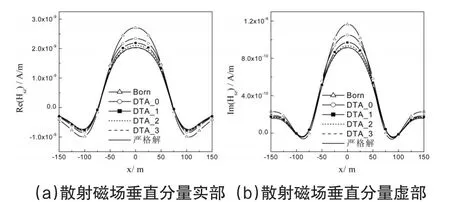
图4 散射体为低阻时的散射场

图5 目标体为高阻时的散射场

4 结论

本文提出了一种计算横向同性分层介质电磁散射问题的高阶DTA级数算法。通过与现有方法对比发现，本文算法对于散射体为低阻和高阻时均具有较高的计算精度，而传统Born近似以及DTA在目标体为低阻时计算精度较低。引入压缩映射的高阶DTA级数收敛很快，只需要较少的阶数就可以接近于严格方法的计算结果，而计算效率却比严格方法有了较大提高。本文方法可用于横向同性分层介质中各种电磁响应特征与规律的系统考察与分析，也可为进行复杂介质中电磁资料的快速三维反演成像提供一套有效正演算法。

［1］Chew W C，Jin J M，Michielsen E，et al.Fast and efficient algorithm in computational electromagnetics［C］.Norwood：Artech House，2001.

［2］Zhdanov M S.Geophysical electromagnetic theory and methods［C］.Amsterdam：Elsevier，2009.

［3］陈桂波，汪宏年，姚敬金，等.用积分方程法模拟各向异性地层三维电性散射体的电磁响应［J］.地球物理学报，2009，52（8）：2174-2181.

［4］Chew W C.Waves and fields in inhomogeneous media［C］.New York：Van Nostrand Reinhold，1990.

［5］Habashy TM，Groom R W，Spies B R.Beyond the Born and Rytov approximations：anonlinearapproach to electromagnetic scattering［J］.Journalof Geophysical Research，1993，98（B2）：1759-1775.

［6］Zhdanov M S，Fang S.Quasi-linear approximation in 3D electromagnetic modeling［J］.Geophysics，1996，61（3）：646-665.

［7］Zhdanov M S，Dmitriev V I，Fang S，et al.Quasi-analytical approximations and series in electromagnetic modeling［J］.Geophysics，2000，65（6）：1746-1757.

［8］SongLP，LiuQH.Anewapproximationto three-dimensional electromagnetic scattering ［J］.IEEE Geoscience and Remote Sensing Letters，2005，2（2）：238-242.

［9］Song L P，Liu Q H.Fast three-dimensional electromagnetic nonlinear inversion in layered media with a novelscattering approximation［J］.Inverse Problems，2004，20（6）：171-194.

［10］陈桂波，汪宏年，姚敬金，等.水平层状各向异性介质中电磁场并矢格林函数的一种高效算法［J］.物理学报，2009，58（3）：1608-1618

［11］Pankratov O V，Kuvshinov A V，Avdeev D B.High-performance three-dimensional electromagnetic modeling using modified Neumann series：Anisotropic earth［J］.J Geomag Geoelectr，1997（49）：1541-1547.