弹箭非线性角运动周期解稳定性分析

钟扬威，王良明，常思江，傅 健

（南京理工大学 能源与动力工程学院，南京210094）

在火箭弹的高原遥测试验中，观测到在大射角射击时出现多次近弹现象，姿态测量结果表明火箭弹在主动段结束时出现约20°左右的大攻角锥形运动。查阅资料发现，美国在进行Nitehawk探空火箭飞行试验时，50多次飞行试验出现了20多次发散的锥形运动。美国的69.85mm机载火箭弹在亚音速及超音速风洞实验时都曾出现发散的锥形运动［1］。西班牙的Ternel 140mm火箭弹28次飞行试验中出现了9次锥形运动，使飞行速度在1.5s内降低了60%［2］。尾翼稳定火箭弹的这些角运动规律用线性理论难以解释，可能是非线性运动造成的。

目前，许多学者对尾翼稳定旋转弹箭的锥形运动稳定性进行了研究。文献［3］研究了卷弧尾翼安装位置对大长径比无控低旋火箭弹锥形运动的影响，证明了通过反装反向卷弧形尾翼可以抑制火箭弹的锥形运动。文献［4］建立了无控低旋火箭弹的锥形运动方程组，并分析了侧向力矩对锥形运动稳定性的影响。文献［5］建立了弹体锥形运动的模型，研究了章动运动对锥形运动极限环的影响。文献［6］研究了大攻角情况下非对称赤道阻尼力矩对远程火箭极限圆锥运动的影响。文献［7－8］基于陀螺线性扰动运动方程研究了旋转导弹的锥形运动稳定性问题。文献［9］对一类低速旋转弹在高空且考虑非线性气动力时的锥形运动稳定性进行了分析。

事实上，弹箭的锥形运动对应于非线性动力学中的周期运动，本文采用非线性动力学中的周期解分岔及稳定性分析等相关理论，基于新的弹箭非线性角运动方程，提出了分析和计算弹箭非线性角运动周期解的方法，为分析弹箭非线性角运动规律提供了理论基础。

1 弹箭非线性角运动方程组

对于弹箭的角运动，主要关心的是攻角δ1，δ2及摆动角速度ωη，ωζ的变化情况。故选取这4个量作为状态变量x＝（δ1δ2ωηωζ）T，根据文献［10］中的弹箭运动方程组，通过推导得到弹箭的非线性角运动方程组：

式中：Fy，Fz分别为弹箭所受的总气动力在速度坐标系相应轴上的投影；m为弹箭的质量；v为弹箭的速度；Mη和Mζ为弹箭所受的合力矩在弹轴坐标系相应轴上的投影；ωξ为弹箭的滚转角速度；JA，JC分别为弹箭的赤道转动惯量和极转动惯量。气动力的计算公式见文献［11］。

将角运动方程写成规范形式，可以表示为＝f（x，μ），其中x∈R4是状态向量；μ∈Rm是分岔参数，是可以表示空气密度、马赫数、弹箭自转速度、气动力和力矩系数等影响弹箭角运动的参数。当选取的参数μ连续变化时，系统的拓扑结构在μ＝μ0处发生突然变化，则称系统在μ＝μ0处出现分岔，并称μ0为一个分岔值。弹箭非线性角运动周期解稳定性分析主要解决两方面的问题：①弹箭角运动是否存在以及何时存在周期解；②周期解的幅值及周期计算和稳定性分析。

2 角运动分岔序列计算

弹箭角运动方程是一个连续性方程，可以通过计算其Poincare映射将其离散化来分析其分岔行为［12］。Poincare映射是研究周期运动及其分岔的几何方法，它将非线性系统转化为与之本质上完全等价而研究起来更为简单方便的点映射系统。Poincare映射的定义如下。

设Γ为系统的周期解，其最小周期为T，过Γ上任意一点x＊作与Γ横截相交的n－1维超曲面。根据流形φt的连续性，存在x＊的某个邻域U⊆Σ，使得U内任何一点出发的轨道都可以在约T的时间内再次回到Σ上，这样就定义了x＊的一个邻域U⊂Σ到Σ的映射P，P称为系统的Poincare映射。

通过Poincare映射可以计算弹箭非线性角运动的分岔序列，其数值算法描述如下。

①选择超曲面Σ。

弹箭角运动方程为非线性自治方程，自治系统没有特定的方法选取Poincare截面，需要根据具体的运动情况进行选取。本文选取弹箭的摆动角速度ωη的导数通过0时的点作为轨道与Poincare截面的交点，即定义

②计算轨道与超曲面的交点。

选取分岔参数μ为某一确定值，对角运动方程进行积分，计算经过每一个步长时的。重复以上步骤，直到连续的2个点｜t＝t1和｜t＝t2位于Σ的两侧，即有相反的符号，则可确定交点位于t1和t2之间的某一点。不断平分区间［t1，t2］直至达到要求的精度。重复上述过程，可求出所给定的任意时间长度内的所有交点。

③计算分岔序列。

连续地改变分岔参数μ，重复步骤②，直到求出所要求的分岔区间的Poincare映射图。将分岔区间内的Poincare映射图叠加即可得到分岔序列。

3 周期解计算及稳定性分析

通过计算角运动的分岔序列得出系统存在周期解，如何迅速求出其周期解的幅值和周期是一个问题。采用龙格库塔法等数值积分方法通过积分来求周期解具有一定的盲目性且只能获得稳定的周期解。因此，在周期解的数值计算时一般不采用直接积分的方法。打靶法是一种常用的求解系统周期解的方法，本文采用推广的打靶法［13－14］获得弹箭非线性角运动周期解的幅值及周期，并通过Floquet理论分析周期解的稳定性。

3.1 角运动周期解数值计算

弹箭角运动的周期是未知的，因此需要将周期作为一个参数一起参与打靶，从而求得角运动的周期解及周期。基于推广的打靶法求取弹箭非线性角运动周期解的步骤如下。

①引入变量τ，变换时间尺度t＝Tτ，角运动方程变为

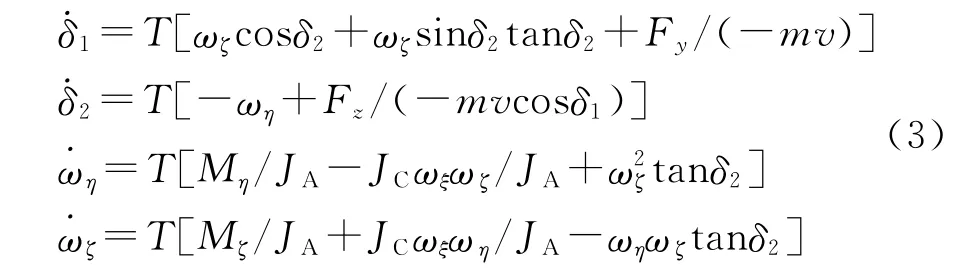
②选取初始迭代向量x0＝从τ＝0到τ＝1对式（3）进行积分，得到系统在周期末时刻的值x1＝），并计算误差向量r，其中：

式中：i，j＝1，…，4；xi，xj分别表示为Kronecker符号。

⑤将步骤④中所求的值代入式（5）中，求得∂ri／，∂ri／∂T0的值。

⑥将ri＝0在xi和T0邻域内作泰勒展开，忽略高阶项，生成的线性方程组为

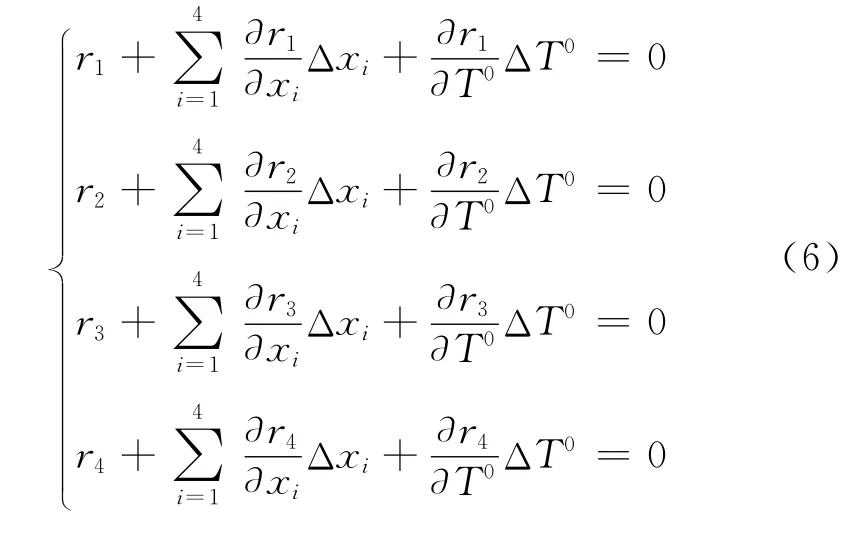
⑧检查步骤⑦求出的增量值是否满足所需的精度要求，若满足则结束迭代，得到角运动的周期解和周期；否则令＝＋Δxi和T0＝T0＋ΔT转第②步继续进行迭代计算。

3.2 周期解稳定性分析方法

Floquet理论是从摄动方程零解稳定性判别未扰动周期运动稳定性的思想得到的稳定性理论，利用它可以分析非线性角运动周期解的稳定性问题［15］。

对于非线性系统的摄动方程：

式中：A（t＋T）＝A（t）是一个周期为T的矩阵函数。若x（t）为方程（7）的一个基本解矩阵，根据Floquet理论，则必存在一个非奇异的T周期矩阵φ（t）＝φ（t＋T）和一个常矩阵D，使得x（t）＝φ（t）etD。因为（t）＝A（t）x（t），则有：

从而

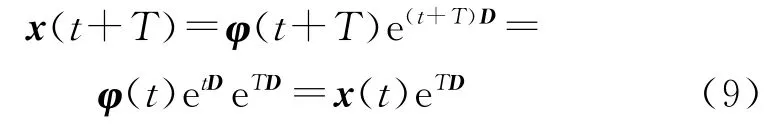
式中：eTD＝C为一常数矩阵，称为系统的离散状态传递矩阵，C的特征值λ称为Floquet乘子。根据定义，状态转移矩阵C可以取为3.1中步骤⑦所计算出的系数矩阵。

可以利用主导Floquet乘子（绝对值最大的Floquet乘子）得到系统周期解的稳定性判据：

①当λ的绝对值小于1时，周期解稳定；

②当λ的绝对值大于1时，周期解不稳定；

③当λ的绝对值等于1时，周期解临界稳定。

4 数值仿真与分析

高原射击时，火箭弹主动段结束后其所处的飞行空域较高，空气密度较低，在持续重力及较小的气动力和气动力矩作用下，容易诱导产生较大的攻角［9］。大攻角飞行时，弹箭的气动系数存在明显的非线性，需要考虑气动系数的非线性项。

文献［11］通过闪光摄影和飞行试验获得了一些弹箭的非线性马格努斯力矩系数，给出了非线性马格努斯力矩的流体动力学机理解释，并指出了弹箭的非线性马格努斯力矩与极限环的运动关系。笔者所在的课题组在进行气动力数值计算时，发现在较大攻角时火箭弹的马格努斯力矩系数存在严重非线性，它随马赫数和攻角的变化较为明显。因此，高原弹箭射击试验中出现的大攻角锥形运动可能是在高空低密度情况下由非线性马格努斯力矩导致的。

根据文献［11］，考虑线性马格努斯力矩系数CMpα0和立方马格努斯力矩系数CMpα2时，马格努斯力矩系数CMpα可表示为以下的多项式形式：

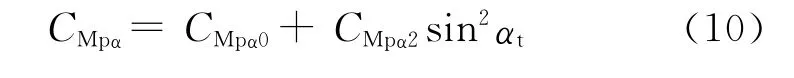
式中：sin2αt＝（sinδ1cosδ2）2＋sin2δ2，αt为总攻角。

以某型火箭弹高原射击时一些参数为主要仿真条件：①弹丸质量45kg，极转动惯量0.115kg·m2，赤道转动惯量30.63kg·m2，弹丸直径0.122m，弹丸长度2.8m；②阵地海拔为4 000m，火箭弹主动段结束时刻飞行速度为1 012.3m／s，弹丸轴向角速度为79.006 4rad／s；③线性升力系数为6.5，线性静力矩系数为－1.254 6，赤道阻尼力矩系数为0.46；④空气密度取0.562 3kg／m3。

取CMpα0＝8，立方马格努斯力矩系数CMpα2分别取10，20，30，40。仿真得到的角运动相图和Poincare截面图如图1所示，图中的＊表示庞加莱截面上的点。

图1 角运动相图

从图1可以看出，CMpα2为正时，庞加莱截面上存在2个点，角运动存在周期解。进一步计算，CMpα2为负时，庞加莱截面上没有点，角运动发散。

取CMpα2＝30，取线性马格努斯力矩系数CMpα0由－10～0变化，仿真得到的Poincare映射分岔图，如图2所示。

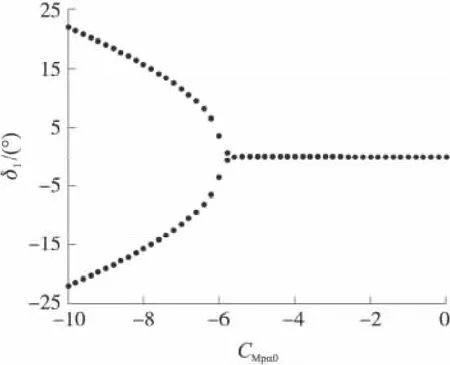
图2 角运动分岔图

由分岔图看出，当CMpα0＞－5.8时，角运动渐进稳定于唯一的零平衡位置；当CMpα0＜－5.8时，零平衡位置不稳定，分岔出周期解，角运动发生Hopf分 岔，CMpα0＝ －5.8 称 为 分 岔 点。CMpα0＜－5.8后，角运动处于周期运动，周期运动的幅值随CMpα0的减小而增大。线性马格努斯力矩系数CMpα0分别取－6，－7，－8，－9时，通过推广的打靶法计算得到的攻角运动周期解如图3所示。由图3可以看出，线性马格努斯力矩系数CMpα0对角运动周期解的幅值影响比较大，CMpα0减小时，周期解幅值增大，与图2得出的结论一致。当线性马格努斯力矩为－9时，攻角运动周期解的幅值约为19°。

图3 角运动周期解

攻角运动周期解的周期T及主导Floquet乘子λ如表1所示。

表1 周期T及主导Floquet乘子λ

由表1可以看出，角运动周期解的周期随线性马格努斯力矩系数CMpα0的变化较小，且主导Floquet乘子λ的绝对值都小于1，说明周期解是稳定的。

5 结束语

本文基于一般形式的弹箭非线性角运动微分方程组，提出了基于Poincare映射的弹箭非线性角运动分岔序列的数值计算方法，给出了通过推广的打靶法计算弹箭角运动周期解的幅值和周期的计算方法，并结合Floquet理论给出了周期解稳定性的分析方法。以某型火箭弹为例，计算分析了立方马格努斯系数作用下的角运动相图及以线性马格努斯力矩系数作为分岔参数时的非线性角运动规律。结果表明，在高空低密度的情况下，当马格努斯力矩系数达到一定的范围时，火箭弹会出现稳定的周期运动。

［1］李臣明，刘怡昕.转速闭锁对远程弹箭的影响［J］.弹道学报，2010，22（1）：45－48.LI Chen－ming，LIU Yi－xin.Effect of roll locking on long－range missile［J］.Journal of Ballistics，2010，22（1）：45－48.（in Chinese）

［2］MOROTE J，LIANO G.Stability analysis and flight trials of a clipped wrap around fin configuration［C］／／AIAA Atmospheric Flight Mechanics Conference and Exhibit.Providence，Rhode Island：AIAA，2004.

［3］王华毕，吴甲生.火箭弹锥形运动的数学仿真与抑制措施［J］.北京理工大学学报，2007，27（3）：196－199.WANG Hua－bi，WU Jia－sheng.Coning motion of rockets，its numerical simulation and restraint［J］.Transactions of Beijing Institute of Technology，2007，27（3）：196－199.（in Chinese）

［4］王华毕，吴甲生.火箭弹锥形运动稳定性分析［J］.兵工学报，2008，29（5）：562－566.WANG Hua－bi，WU Jia－sheng.The coning motion stability analysis of rocket［J］.Acta Armamentarii，2008，29（5）：562－566.（in Chinese）

［5］闫晓勇，杨树兴，张成.基于章动运动理论的火箭弹锥形运动稳定性分析［J］.兵工学报，2009，30（10）：1 291－12 96.YAN Xiao－yong，YANG Shu－xing，ZHANG Cheng.Analysis of stability for coning motion of rockets based on theory of nutation movement［J］.Acta Armamentarii，2009，30（10）：1 291－1 296.（in Chinese）

［6］李臣明，刘怡昕.非对称赤道阻尼力矩对远程火箭弹道的影响［J］.弹道学报，2009，21（2）：36－39.LI Chen－ming，LIU Yi－xin.Effect of roll locking on long－range missile［J］.Journal of Ballistics，2009，21（2）：36－39.（in Chinese）

［7］任天荣，马建敏.基于陀螺力学的旋转导弹锥形运动分析［J］.宇航学报，2010，31（9）：2 082－2 087.REN Tian－rong，MA Jian－min.Coning motion analysis of spinning missile based on gyro dynamics［J］.Journal of Astronautics，2010，31（9）：2 082－2 087.（in Chinese）

［8］任天荣，马建敏.旋转弹锥形运动发生区间及频率特性研究［J］.固体火箭技术，2014，37（3）：295－300.REN Tian－rong，MA Jian－min.Research on activating region and frequency characteristics of coning motion for spinning missiles［J］.Journal of Solid Rocket Technology，2014，37（3）：295－300.（in Chinese）

［9］李克勇，赵良玉，周伟.一类旋转弹在高空中的锥形运动稳定性［J］.动力学与控制学报，2012，10（3）：239－243.LI Ke－yong，ZHAO Liang－yu，ZHOU Wei.Stability of conig motion of spinning rocket projectiles at high altitude［J］.Journal of Dynamic and Control，2012，10（3）：239－243.（in Chinese）

［10］韩子鹏.弹箭外弹道学［M］.北京：北京理工大学出版社，2014.HAN Zi－peng.Exterior ballistics of projectiles and rockets［M］.Beijing：Beijing Institute of Technology Press，2014.（in Chinese）

［11］ROBERT L.Modern exterior ballistics［M］.Atglen，Pennsylvania：Schiffer Publishing Ltd，1999：273－298.

［12］吴志强，张建伟.二元机翼极限环颤振复杂分岔［J］.工程力学，2008，25（2）：52－56.WU Zhi－qiang，ZHANG Jian－wei.Complicated bifurcation in limit cycle flutter of two dimensional airfoil［J］.Engineering Mechanics，2008，25（2）：52－56.（in Chinese）

［13］ROOSE D，LUST K，CHAMPENEYS A.A Newton－Picard shooting method for computing periodic solutions of large－scale dynamical systems［J］.Chaos，Solitons ＆ Fractals，1995，5（10）：1 913－1 925.

［14］李德信，徐健学.求解非线性动力系统周期解推广的打靶法［J］.应用力学学报，2003，20（4）：80－86.LI De－xin，XU Jian－xue.The generalized shooting method for solving the periodic solutions of nonlinear dynamical system［J］.Journal of Applied Mechanics，2003，20（4）：80－86.（in Chinese）

［15］张家忠.非线性动力系统的运动稳定性、分岔理论及其应用［M］.西安：西安交通大学出版社，2010.ZHANG Jia－zhong.Motion stability，bifurcation theory and its application of nonlinear dynamical systems［M］.Xi’an：Xi’an Jiao Tong University Press，2010.（in Chinese）