降雨条件下顺层岩质边坡破坏模式及稳定性研究
刘平军
(贵州交通岩土工程有限责任公司 贵阳 550081)
降雨条件下顺层岩质边坡破坏模式及稳定性研究
刘平军
(贵州交通岩土工程有限责任公司贵阳550081)
摘要在降雨入渗过程中,顺层岩质边坡后缘张裂隙的充水高度应由汇入流量与地下水在层面渗流时的渗流量所共同决定。通过分析降雨作用下顺层岩质边坡的滑移-拉裂破坏模式,建立了地下水渗流量与汇入流量和张裂隙充水量之间的关系,并推导了边坡稳定性系数与降雨强度的计算公式,编制了相应的计算程序。并以某高速公路路堑边坡为例,与不考虑层面渗流量的方法进行对比分析。结果表明,文中方法能够较好地反映边坡稳定性随降雨强度而变化的程度。
关键词地下水顺层岩质边坡破坏模式稳定性计算
顺层岩质边坡是交通、矿山、水电等工程领域中经常出现的边坡地质体,对其破坏机理及稳定性的分析也一直是研究的热点问题。顺层岩质边坡是指边坡的岩层倾向于斜坡面,且倾斜方向一致或接近的边坡。降雨是造成顺层边坡破坏的主要诱发因素之一,不同的降雨量和降雨持时对边坡的稳定性会有不同程度的影响,主要有以下几个方面:①降雨入渗后增加了岩体的重量,导致坡体的下滑力增加;②降雨入渗后沿坡面方面的渗流及在裂隙中形成的静水压力会增加边坡的下滑力;③水对岩体有一定的软化作用,会降低岩体及结构面的强度,致使抗滑力减小。
目前,对于降雨作用下的顺层岩质边坡稳定性问题一些学者进行了一定的研究。刘玉梅[1]推导了后缘张裂型顺层岩质边坡在地下水作用下的稳定系数计算公式;刘才华[2]认为后缘张裂型顺层岩质边坡在降雨过程中,裂隙的充水高度与后缘的汇入流量正相关,并推导了降雨强度和张裂隙充水高度之间的计算公式。在实际的降雨入渗过程中,后缘张裂隙的充水高度不仅取决于汇入流量,而且还应考虑地下水在层面渗流时的渗流量。基于此,本文首先分析降雨作用下顺层岩质边坡的滑移-拉裂破坏模式,然后建立了地下水渗流量与汇入流量和张裂隙充水量之间的关系,继而推导了边坡稳定性系数与降雨强度的计算公式,通过编制相应的计算程序以某高速公路路堑边坡为例,对比分析本文方法与不考虑层面渗流量之间的结果。
1降雨作用下顺层岩质边坡的破坏模式
大量的边坡实例[3-5]表明,降雨对边坡的稳定性有至关重要的作用。降雨作用下顺层岩质边坡的平面破坏形式根据其变形破坏的力学机制可分为2种地质力学模式:滑移-拉裂型与滑移-弯曲型。
滑移-拉裂型边坡的变形破坏主要发生在边坡已形成后缘拉裂缝、倾角不大于30°的中等倾角顺层岩质边坡中。边坡由于开挖等因素使得坡体初始应力状态发生改变,坡顶一定范围内会产生卸荷裂隙。在降雨过程中,雨水会汇入卸荷裂隙中,继而产生静水压力,使得卸荷裂隙进一步向下扩展,当扩展到一定程度时,与层面形成完整的渗流系统。滑坡体内的地下水使得坡体中力学性质裂化,进而当渗流层面的抗剪强度小于坡体剪切应力时,斜坡岩体将沿渗流层面向临空面方向滑动,并使滑移体拉裂解体,见图1。根据极限平衡原理,可以计算顺层岩质边坡岩层失稳横向极限长度,由此进行顺层推力计算,详细计算过程见相关研究[6-7]。

图1 滑移-拉裂破坏模式[8]
2降雨作用下顺层岩质边坡的稳定性分析
岩质边坡水力学理论是基于土质边坡水力学,并继承了土质边坡水力学的一般规律。但由于岩质边坡的地质结构与土质边坡截然不同,地下水在二者中的赋存环境差异很大,这就决定了地下水对岩质边坡的水力学作用方式及边坡稳定性的影响规律有别于土质边坡。
图2为具有后缘张裂隙的典型岩质边坡,在降雨初期,后缘张裂隙中汇入的地表水首先会沿着层面渗流,最终表现为作用在层面沿渗径方向的面力,即拖曳力。随着降雨的继续,张裂隙中的裂隙水量大于层面的渗流量,继而产生静水压力,包括后缘张裂隙静水压力和层面上的扬压力。
岩质边坡中层面内的渗流,不考虑地下水流动时的惯性力,地下水产生渗透压力最终转化为作用在岩层上下壁面上的拖曳力,由静力平衡方程可得拖曳力为

(1)
式中:b为结构面宽度;γw为水的重度;I为沿渗流方向的水力梯度。
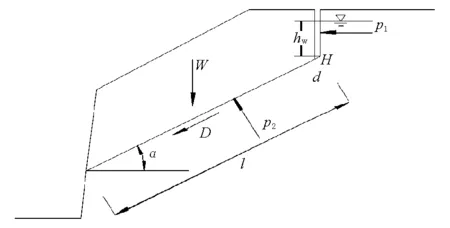
图2 滑移-拉裂型边坡稳定性分析模型
由于岩层上下面的物理力学特征相似,在边坡稳定性分析中,取地下水渗流对层面上部岩体的拖曳力为总拖曳力的一半,则地下水渗流对层面上部岩体的拖曳力t为
(2)
由岩体水力学理论可知,图2所示顺层边坡地下水在层面中渗流时的流量为
(3)
式中:k为层面渗透系数;b为层面宽度。
张裂隙汇流量可按如下公式计算[9]
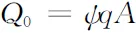
(4)
式中:ψ为径流系数;q为降雨强度;A为汇水面积。
在降雨入渗的整个过程中,张裂隙中的总汇流量应等于层面的渗流量和张裂隙内剩余流量之和,即Q0=Q+hwbd
(5)
式中:d为裂隙宽度。
则,张裂隙内充水高度hw为
(6)
根据图2所示的稳定性分析模型,作用在潜在滑体上的力有:滑体自重为W、后缘垂直张裂隙静水压力为p1、滑动面孔隙水扬压力为p2和拖曳力为D、滑面倾角为α、滑面长度为l、后缘张裂隙充水高度为hw。
后缘张裂隙充水后,后缘垂直张裂隙静水压力p1为
(7)
层面上的扬压力沿层面法向作用,扬压力p2为
(8)
结构面的拖曳力沿滑动方向向下作用,增加了边坡的下滑力D,由式(8)可知其表达式为
(9)
根据沿滑动方向的极限平衡关系式,可得边坡稳定性系数Fs为
(10)
3工程应用
3.1 工程概况
滑坡地点位于杭瑞高速公路(贵州境内遵义—毕节19合同段)YK1724+620~YK1724+733,该边坡为硬岩顺向坡,岩性为二叠系下统茅口组(P1m)灰岩,滑坡前缘为褐黄色粉质粘土。滑坡体内发育一逆断层F1,宽2~3 m,沿滑坡左侧后缘于YK1724+730处穿过轴线,断层产状为60°∠80°,其上盘岩层产状为130°∠28°,下盘岩层产状为150°∠20°。边坡先后进行了2次开挖,开挖期间因连续多次暴雨,滑坡体后缘与母岩产生脱离,后缘产生大裂缝,裂缝宽10 m,深8 m,倾角85°,现滑坡处于蠕动状态,仍在继续向路线方向滑移,工程地质剖面图见图3。

图3 A-A′剖面图
3.2 计算模型及参数
滑坡计算模型见图4,计算参数如下:滑动层面天然粘聚力c=15 kPa,天然内摩擦角φ=16°;饱和粘聚力c′=12 kPa,饱和内摩擦角φ′=13°。滑面长度l1,l2=27 m、42 m,宽度b为1.3 cm,渗透系数k为1.53 m/s,张裂隙横向汇流宽度9.25 m,径流系数ψ= 0.6,滑坡发生的暴雨强度q=9.4 mm/h。

图4 滑坡计算模型
3.3 稳定性计算结果分析
该滑坡属中型-牵引式-顺层岩质滑坡,局部层间夹软弱层,后缘有一逆断层通过,受断层影响,其附近岩体较破碎,岩溶较发育。边坡前缘进行开挖坡脚后,破坏了原坡体的平衡条件,加之近期连续降雨,导致坡体内岩土物理力学性质变差,从而形成大规模变形。
根据计算式(10),编制相应的稳定性计算程序。以降雨强度为变量计算得到不同降雨强度下的边坡稳定性情况,见图5。

图5 不同降雨强度与边坡稳定性关系曲线图
由图5可见,边坡的稳定性随着降雨强度的增加而降低,具体来说,在小雨至中雨阶段边坡的稳定性成指数形降低,在中雨至大雨阶段,边坡稳定性变化趋势成线性,在大雨至暴雨阶段,边坡稳定性处于临界状态。边坡2次开挖均有降雨,第1次开挖时,边坡有一定程度的变形,1 h降雨强度约为q=8.4 mm/h,对应图5的稳定性系数可知,其值接近于极限平衡值,处于潜在不稳定状态;第2次开挖时,滑坡发生的1 h降雨强度为q=9.6 mm/h,对应图5的稳定性系数小于1,属于不稳定性状态。本文的稳定性计算公式能较正确地反映边坡随降雨强度而变化的程度。
同一降雨强度下,对比分析考虑与不考虑层面渗流量的边坡稳定性情况,见表1。

表1 不同降雨强度下2种方法的稳定性系数值
由表1可见,在降雨强度为8 mm/h时,本文方法的稳定性系数为1.30,不考虑层面渗流的计算结果为1.13;在滑坡发生的降雨强度为9.6 mm/h时,本文方法的稳定性系数为0.92,而不考虑层面渗流的计算结果为0.79。由此说明,不考虑层面渗流的稳定性系数普遍较本文方法有所减小,主要原因在于不考虑层面渗流时,其张裂隙的充水高度比本文方法的充水高度要高,所提供的下滑力较大所致。因此,考虑层面渗流的稳定性计算公式能够较真实地反应边坡实际的稳定性情况。
4结论
(1) 计算顺层边坡后缘拉裂缝的充水高度时,不仅需要考虑汇入流量,而且还应考虑地下水在层面渗流时的渗流量。通过与不考虑层面渗流量的计算结果对比可以看出,本文方法更符合实际情况。
(2) 通过分析边坡稳定性系数与坡体内水力情况的关系,给出了以降雨强度考虑边坡稳定性情况的依据,具有一定的工程应用价值。
参考文献
[1]刘玉梅,杨振凯.饱水岩体边坡抗滑稳定系数计算[J].岩土力学,2003,24(S):329-331.
[2]刘才华,徐健,曹传林,等.岩质边坡水力驱动型顺层滑移破坏机制分析[J].岩石力学与工程学报,2005,24(19):3529-3533.
[3]何满朝,姚爱军,鹿粗.边坡岩体水力学作用的研究[J].岩石力学与工程学报,1998,17(6):662-666.
[4]刘才华,陈从新,冯夏庭.地下水对库岸边坡稳定性的影响[J].岩土力学, 2005,26(3):419-422.
[5]何满朝,姚爱军,鹿粗.边坡岩体水力学作用的研究[J].岩石力学与工程学报,1998,17(6):662-666.
[6]邓荣贵,周德培,李安洪,等.顺层岩质边坡不稳定岩层临界长度分析[J].岩土工程学报,2002,24(2):178-181.
[7]冯君,周德培,江南,等.顺层岩质边坡顺层滑动岩体范围分析[J].山地学报, 2007,25(3):376-379.
[8]张倬元,王士天,王兰生.工程地质分析原理[M].北京:地质出版社,1994.
[9]JT J018-97公路排水设计规范[S].北京:人民交通出版社, 1997.

Study on the Bedding Rock Slope Failure Mode and Stability Under the Condition of Rainfall
LiuPingjun
(Guizhou Transportation Geotechnical Engineering Co.,Ltd., Guiyang 550081, China)
Abstract:In the actual process of rainfall infiltration, the water filling height of bedding rock slope trailing edge tension fissure should be decided by import flow and seepage flow when underground water in the level of seepage. Through analyzing the sliding-tension failure mode of bedding rock slope under the condition of rainfall, we established the relationship between the groundwater seepage, import flow and the tension fissure filling water., A formula to calculate the coefficient of stability of slope and rainfall intensity was derived. The corresponding calculation program was compiled. We comparatively analyzed considering the level seepage flow method or not considering the level seepage flow method based on highway cutting slope. Results show that this method can better reflect the slope stability varies with rainfall intensity degree.
Key words:underground water; bedding rock slope; failure mode;stability calculation

