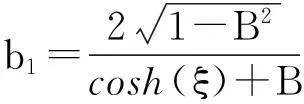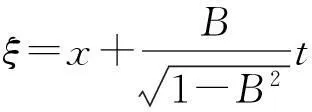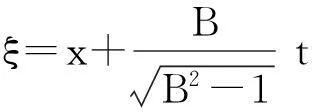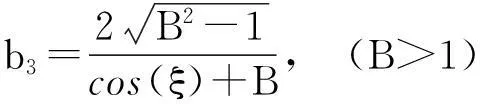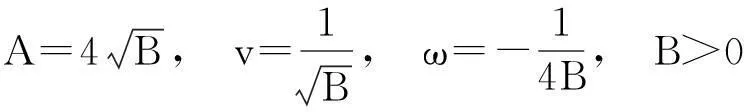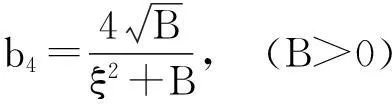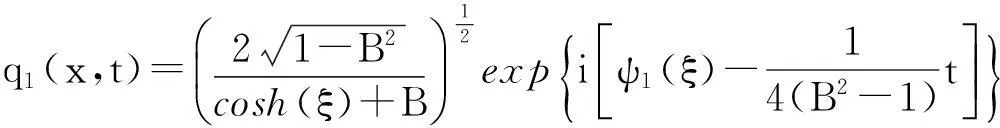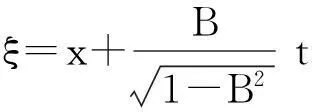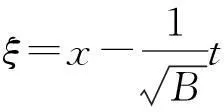简化齐次平衡原则与Gerdjikov-Ivanov方程的精确解
简化齐次平衡原则与Gerdjikov-Ivanov方程的精确解
李向正1,郝祥晖2
(1.河南科技大学 数学与统计学院,河南 洛阳 471023;2.济源职业技术学院 基础部,河南 济源 459000)
摘要:发展和改进求解非线性发展方程的方法是一项重要的工作。简化了齐次平衡原则,用变化后的方法求解了Gerdjikov-Ivanov方程,得到了该方程的钟状孤波解、周期波解和代数孤波解。
关键词:Gerdjikov-Ivanov方程;齐次平衡原则;精确解
基金项目:国家自然科学基金项目(10871129);河南省教育厅自然科学研究计划基金项目(2011B110013,12B110006);河南科技大学博士科研启动基金项目(09001562)
作者简介:李向正(1972-),男,河南偃师人,副教授,博士,主要研究方向为非线性数学物理方程.
收稿日期:2014-06-06
文章编号:1672-6871(2015)01-0082-04
中图分类号:O175.2
文献标志码:A
0引言
现代物理学的进展在很大程度上依赖于非线性数学及求解非线性方程方法的进展[1]。文献[2-3]提出齐次平衡原则之后,该原则在非线性发展方程的求解方面得到了广泛的应用。已有的一些行之有效的方法,诸如双曲正切函数展开方法[4]及其扩展方法[5]、Jacobi椭圆函数展开方法[6]、F展开法[7-9]、(G′/G)展开法[10-14]、LS解法[15]、映射法[16]、辅助方程法[17-18]等,均需借助齐次平衡原则来确定其解的表达式中最高次项的次数。然而,齐次平衡原则中有一些步骤是可以简化的。本文将对齐次平衡原则进行简化以及变形,并以Gerdjikov-Ivanov方程
(1)
为例,求出其精确解。此方程出现在量子场理论、弱非线性色散水波和非线性光学等领域。文献[19]借助Liénard方程作辅助求解了方程(1)。文献[20]用分支理论和相图分析的方法研究了方程(1),并给出了部分精确解。
1Gerdjikov-Ivanov方程的精确解
下面寻找方程(1)的行波解:
q(x,t)=a(ξ)exp{i[ψ(ξ)-ωt]},
(2)
其中:x为空间变量;t为时间变量;q(x,t)为光波的振幅函数;ξ=x-vt,v为待定常数;a(ξ)>0;ψ(ξ)为待定实函数;ω为待定常数。
将式(2)代入方程(1),消去因子exp{i[ψ(ξ)-ωt]},并令实部虚部分别为零,得到a(ξ),ψ(ξ)满足的常微分方程(ODE)组:
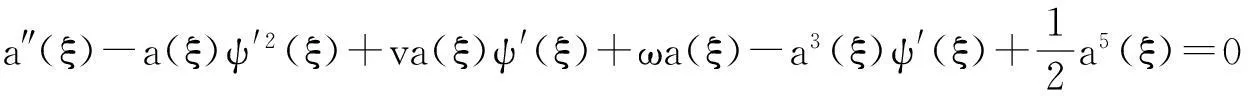
(3)
-va′(ξ)+2a′(ξ)ψ′(ξ)+a(ξ)ψ″(ξ)-a2(ξ)a′(ξ)=0。
(4)
为简化方程组(3)和方程组(4),令
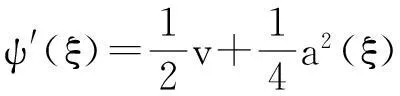
(5)
将式(5)代入式(4),可使式(4)自动成立。将式(5)代入式(3)得:
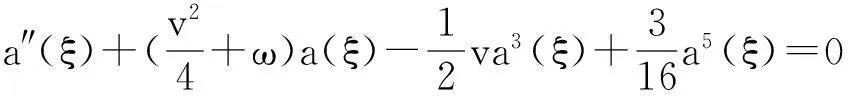
(6)
设
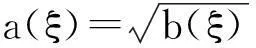
(7)
将式(7)代入方程(6),整理可得:
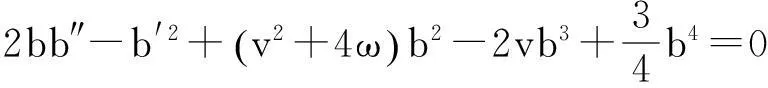
(8)
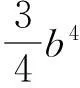

(9)
其中,A、B是待定常数。
将式(9)代入方程(8),得:

(4A2v2+16A2ω)f2+12A2f′2-8A2Bf″-8A2ff″]=0。
(10)
要使方程(10)成立,只需
3A4-8A3Bv+4A2B2v2+16A2B2ω+(-8A3v+8A2Bv2+32A2Bω)f+
(4A2v2+16A2ω)f2+12A2f′2-8A2Bf″-8A2ff″=0。
(11)
下面考虑方程(11)3种形式的解:
(Ⅰ)设f=cosh(ξ)。
(12)
将式(12)代入方程(11),而后令cosh(ξ)各幂次项的系数为零,解关于A、B、v和ω的方程组得:
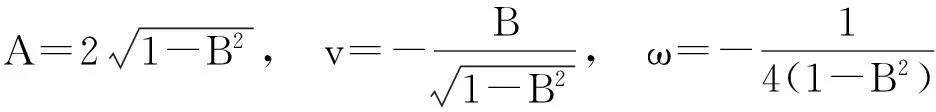
(13)
其中,0 将式(12)和解(13)代入式(9)得: (14) (Ⅱ)设f=cos(ξ)。 (15) 将式(15)代入方程(11),而后令cos(ξ)各幂次项的系数为零,解关于A、B、v和ω的方程组得: (16) 其中,B2>1。 将式(15)和解(16)代入式(9)得: (17) (18) (Ⅲ)设f=ξ2。 (19) 将式(19)代入方程(11),而后令ξ2各幂次项的系数为零,解关于A、B、v和ω的方程组得: (20) 将式(19)和解(20)代入式(9)得: (21) 将b1、式(7)及解(13)代入式(5),再积分后解出: (22) 再将b1、式(7)、解(13)及式(22)代入式(2),可得方程(1)的钟状孤波解: (23) 将b2、式(7)及解(16)代入式(5),再积分后解出: (24) 再将b2、式(7)、解(16)及式(24)代入式(2),可得方程(1)的周期波解: (25) 将b3、式(7)及解(16)代入式(5),再积分后解出: (26) 再将b3、式(7)、解(16)及式(26)代入式(2),可得方程(1)的周期波解: (27) 将b4、式(7)及解(20)代入式(5),再积分后解出: (28) 再将b4、式(7)、解(20)及式(28)代入式(2),可得方程(1)的代数孤立波解: (29) 本文借助方程(10)的解来构造Gerdjikov-Ivanov方程的精确解,此方法与文献[19]对比,其思想更自然。文献[20]利用直接积分法构造方程(1)的解,需要较高的技巧,不如本文方法简洁。需要指出的是复函数的模一般为正值,文献[20]中给出的负值的模函数应舍去。 2结论 本文对齐次平衡原则做了3点变化。首先,直接将齐次平衡原则中的待定函数改为有理函数,并相应省去了原方法中的第2步和第3步,减少了计算量;其次,将变化后的齐次平衡原则直接作用于行波约化后的非线性常微分方程,再将问题转化为求解齐次平衡的常微分方程;第三,原齐次平衡原则中没有给出式(5)的解,借助式(5)可得到方程(1)的钟状孤波解、周期波解和代数孤波解。本文以Gerdjikov-Ivanov方程为例,证明了简化齐次平衡原则是可行且有效的。 致谢:本文得到王明亮教授的指导,在此表示感谢。 参考文献: [1]Joel S.Shock Waves and Reaction-diffusion Equations[M].New York:Springer-Verlag New York Inc,1983. [2]Wang M L.Solitary Wave Solutions for Variant Boussinesq Equations[J].Phys Lett A,1995,199:169-172. [3]Wang M L,Zhou Y B,Li Z B.Application of a Homogeneous Balance Method to Exact Solutions of Nonlinear Equations in Mathematical Physics[J].Phys Lett A,1996,216:67-75. [4]Lan H B,Wang K L.Exact Solutions for Two Nonlinear Equations[J].J Phys A:Math Gen,1990(23):4097-4105. [5]Fan E G,Zhang H Q.A Note on Homogeneous Balance Method[J].Phys Lett A,1998,246(5):403-406. [6]Liu S K,Fu Z T,Liu S D,et al.Jacobi Elliptic Function Expansion Method and Periodic Wave Solutions of Nonlinear Wave Equations[J].Phys Lett A,2001,289:69-74. [7]Wang M L,Zhou Y B.The Periodic Wave Solutions for the Klein-Gordon-Schrödinger Equations[J].Phys Lett A,2003,318:84-92. [8]Zhou Y B,Wang M L,Wang Y M.Periodic Wave Solutions to a Coupled KdV Equations with Variable Coefficients[J].Phys Lett A,2003,308:31-36. [9]李向正,张金良,王跃明,等.非线性Schrodinger方程的包络波解[J].物理学报,2004,53(12):4045-4051. [10]Wang M L,Li X Z,Zhang J L.The (G′/G)-expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics[J].Phys Lett A,2008,372(4):417-423. [11]Wang M L,Zhang J L,Li X Z.Application of the (G′/G)-expansion to Travelling Wave Solutions of the Broer-Kaup and the Approximate Long Water Wave Equations[J].Applied Mathematics and Computation,2008,206:321-326. [12]Zhao Y L,Liu Y P,Li Z B.A Connection Between the (G′/G)-expansion Method and the Truncated Painleve Expansion Method and Its Application to the mKdV Equation[J].Chin Phys B,2010(19):030306. [13]李向正.Sawada-Kotera方程的两类孤立波解[J].河南科技大学学报:自然科学版,2014,35(2):78-81. [14]李保安,李灵晓.简化变形Ostrovsky方程的精确解[J].河南科技大学学报:自然科学版,2014,35(2):82-85. [15]李向正,张卫国,原三领.LS解法与Fisher方程行波系统的定性分析[J].物理学报,2010,59(2):744-749. [16]Wu G J,Han J H,Zhang W L.New Periodic Wave Solutions to Generalized Klein-Gordon and Benjamin Equations[J].Commun Theor Phys,2007,48(5):815-819. [17]Sirendaoreji,Sun J.Auxiliary Equation Method for Solving Nonlinear Partial Differential Equations[J].Phys Lett A,2003,309:387-396. [18]Li X Z,Wang M L.A Sub-ODE Method for Finding Exact Solutions of a Generalized KdV-mKdV Equation with High-order Nonlinear Terms[J].Phys Lett A,2007,361:115-118. [19]李向正,李修勇,赵丽英,等.Gerdjikov-Ivanov方程的精确解[J].物理学报,2008,57(4):2031-2034. [20]He B,Meng Q.Bifurcations and New Exact Travelling Wave Solutions for the Gerdjikov-Ivanov Equation[J].Commun Nonlinear Sci Numer Simulat,2010,15:1783-1790.