结构动力响应灵敏度分析伴随法一致性问题研究

第一作者胡智强男，博士生，1984年12月生

通信作者马海涛男，教授，博士生导师，1962年生

结构动力响应灵敏度分析伴随法一致性问题研究

胡智强1,马海涛1,2

(1.华南理工大学土木与交通学院亚热带建筑科学国家重点实验室，广州510640；2.大连理工大学工业装备结构分析国家重点实验室，大连116023)

摘要：研究结构瞬态动力响应灵敏度分析伴随法可能存在的一致性问题，具体考虑先微分后离散与先离散后微分两种敏度分析方法的计算精度、收敛速度及一致性等。基于动力响应分析的时域显式法基本思想，以更简洁方式推导先离散后微分的伴随法计算列式。结果表明，先微分后离散伴随法一致性问题是由计算中所用动力响应结果仅在离散时间点满足运动方程产生的，存在的一致性问题不影响该方法的可靠性及应用。

关键词：灵敏度分析；伴随法；一致性；瞬态动力响应

基金项目：国家自然科学基金(11372004)；工业装备结构分析国家重点实验室(大连理工大学)(GZ1305)

收稿日期：2014-07-16修改稿收到日期：2014-09-25

中图分类号:TU311.3；O342

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.028

Abstract:The inconsistency issue of adjoint variable methods (AVMs) for sensitivity analysis of transient dynamic responses was investigated. The differentiate-then-discretize and discretize-then-differentiate approaches were considered, focusing on their computational accuracy, convergence rates and result consistency. Based on the basic idea of the explicit time-domain method for dynamic analysis, a concise discretize-then-differentiate AVM formulation was presented. It is found that the inconsistency of the differentiate-then-discretize approach is caused by the fact that numerical solutions for dynamic responses satisfy equations of motion only at integration points in the time domain. However, despite this consistency problem, this approach is still reliable for sensitivity analysis of dynamic responses.

On the consistency issue of adjoint methods for sensitivity analysis of dynamic responses

HUZhi-qiang1,MAHai-tao1,2(1. State Key Laboratory of Subtropical Building Science, School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China;2. State Key Laboratory of Structural Analysis of Industrial Equipment, Dalian University of Technology, Dalian 116023, China)

Key words:sensitivity analysis; adjoint variable method; consistency; transient dynamic response

灵敏度分析用于定量预测结构参数变化对响应影响，在结构优化、系统辨识等研究中具有重要作用[1-4]。据计算方式不同，灵敏度分析方法主要分为直接法、伴随法(伴随变量方法)。对参数变量数目较多、所需考虑的响应量较少的一类问题，伴随法的计算效率高于直接法，因此应用更广[5-8]。Keulen等[9]依据精度与一致性、计算量及实现难度三项准则，对线性问题的不同灵敏度分析算法进行总结与评述。

灵敏度方程推导会涉及对结构参数的微分运算。对瞬态动力问题，响应计算涉及时间域的离散化，因此灵敏度分析方法一般存在先微分后离散或先离散后微分两种方式。对直接法，采用此两种方式所得动力响应灵敏度结果相同；但对伴随法，微分、离散的先后次序会影响灵敏度分析结果。Jensen等[10]用单自由度模型研究先微分后离散、先离散后微分的两种灵敏度分析伴随法认为，先微分后离散伴随法会给出不一致的灵敏度结果，相应误差须通过适当选择时间步长及数值求积公式控制，而彻底解决此问题可用先离散后微分算法。

针对一致性问题，本文全面研究动力响应灵敏度分析伴随法的基本问题，包括一致性及收敛速度等。即总结一致性问题提法，简要归纳瞬态动力响应分析的Newmark-β方法及先微分后离散的灵敏度分析伴随法，明确一致性问题根源。并基于动力响应计算时域显式法基本思想，给出先离散后微分的伴随法灵敏度计算列式，针对单自由度、多自由度问题通过两算例研究两种伴随法灵敏度计算精度及收敛性。

1问题提出

灵敏度分析算法选择应依据精度与一致性、计算量及实现难度三项准则。文献[9]将灵敏度分析结果误差分为两类，一类为离散系统的数值解与精确值偏差，用精度表示；一类为计算灵敏度与相对精确数值解的偏差，用不一致性表示。

为简便，考虑离散结构系统动力问题。以动力响应Φ为例，分别用Φa(t,b)及Φd(t,b,Δt)表示精确解、数值解。其中b为某结构参数；t为时间；Δt为时间步长。响应灵敏度可定义为

(1)

(2)

由于数值解存在离散误差，解析解Φa(t,b)与数值解Φd(t,b,Δt)之间存在差别，由式(1)、(2)给出的灵敏度结果会不同，误差由时间离散误差引起。为考察灵敏度分析方法的准确性、一致性，按文献[9-10]，在相同时间离散情况下，若某个灵敏度分析方法给出的结果为gs(t,b,Δt)，则可定义两种误差为

ε=gs(t,b,Δt)-ga(t,b)

(3)

εc=gs(t,b,Δt)-gd(t,b,Δt)

(4)

式中：ε为计算灵敏度与精确解差别；εc为计算灵敏度与目标离散数值解差别。

显然，误差ε反映计算精度，其数值大小反映敏度分析方法的准确性；而误差εc为该灵敏度分析方法计算结果与所得数值解偏差，称为一致性误差。

若某灵敏度分析方法给出的结果存在较大一致性误差，该结果无法准确反映参数变化影响，会造成后续计算效率降低及最终结果偏差。虽常规基于先微分后离散的伴随法计算结果有一致性误差，但仍未见理论解释。为避免不一致灵敏度分析方法产生的影响，文献[7]在瞬态优化中选择用一致灵敏度分析算法，而文献[10]则认为可选先离散后微分的伴随法。对此，本文研究一致性问题产生的根源及对结果影响，加深对该问题的理解、认识，有助于灵敏度分析方法的理论、应用研究。

2结构动力响应计算与灵敏度分析

线性离散结构动力系统运动方程可表示为

(5)

2.1动力方程的数值解法

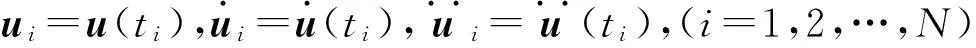
(6)

用Newmark-β法[11]，其逐步积分列式为

(7)

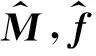
(8)

(9)

2.2动力响应函数及灵敏度分析的伴随法

对动力问题，将响应函数取成一般积分形式，即

(10)

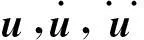
为计算响应函数Φ的灵敏度，引入n维伴随变量向量λ(t)，n为结构自由度数，并定义函数Η为

(11)

由于式(5)在任意时刻均成立，响应函数Φ恒等于Η。因此，两函数偏导数也应恒等。对式(11)微分，再进行分部积分，整理后得

(12)

为消除上式中含响应偏导数的各项，引入关于伴随向量λ(t)的微分方程为

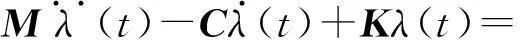
(13)

设初始响应与结构参数无关，据式(12)后两项引入λ(t)应满足的终值条件为

(14)

采用变量代换s=T-t，将式(13)、(14)的终值问题转化成初值问题，即

(15)

(16)

求解式(15)可确定伴随变量Λ(t)，再由式(12)得响应函数Φ对结构参数的灵敏度为

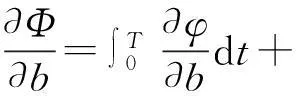
(17)

2.3灵敏度分析伴随法应用与一致性问题

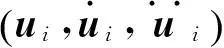
(18)

由于式(18)用时刻点t=T-si处动力响应，故采用Newmark-β法即可获得不同时刻点伴随向量(Λi)。此时，用梯形积分公式[12]可计算式(17)积分，即

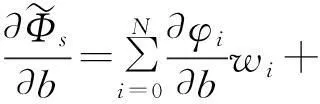
(19)

式中：wi为数值积分权重，分别为w0=0.5Δt，w1=…=wN-1=Δt及wN=0.5Δt。

为获得灵敏度计算公式，对连续响应函数进行微分运算再推导获得伴随方程，方可在时域内离散求解方程。因此将其称为先微分后离散的伴随法。

需要注意的是，按解析推导过程要求，伴随向量计算采用的动力响应结果应在整个时域内满足平衡方程。但式(18)中所用动力响应值仅在离散时间点处满足式(6)，因此响应函数Φ并不恒等于Η，以此为基础所得伴随向量及再由式(19)计算的灵敏度结果会存在偏差。将式(11)两端同时对b求偏导，得

(20)

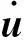
(21)

至此，以推导的灵敏度分析方法为基础，采用数值计算方式可实现先微分后离散伴随法；但该算法存在一致性问题，由于响应的数值解无法满足解析的假设条件，计算所得灵敏度结果会存在一致性误差。本文将通过两算例具体研究此误差对灵敏度计算精度及收敛速度影响。

2.4先离散后微分的灵敏度分析伴随法

文献[10]认为先微分后离散伴随法会给出不一致的灵敏度结果，而先离散后微分的伴随法则不存在一致性问题。本文基于动力响应计算的时域显式法[13]基本思想，以更简洁方式给出先离散后微分的伴随法计算列式。采用逐步积分法计算获得各时刻点动力响应后，可用梯形积分公式计算式(10)的响应函数，即

(22)

(23)

(24)

式中：

(25)

(26)

(27)

(1≤i≤N-1)

(28)

(29)

(30)

由时域逐步积分法获得各时刻点动力响应后，对响应函数计算各时刻点的伴随向量，再用上式计算对不同结构参数的灵敏度信息。

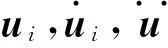
3数值算例

利用单、多自由度两个算例，对比、讨论两种伴随法的计算精度及收敛速度，说明一致性问题的存在不影响先微分后离散伴随法的可靠性及应用。

3.1单自由度系统

图1　单自由度振子模型 Fig.1 The model of single dof oscillator

考虑三种不同形式响应函数，即

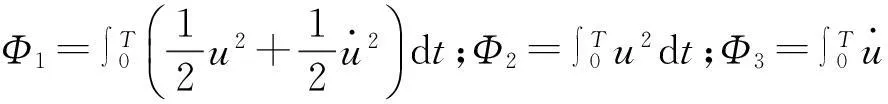
对比响应函数与灵敏度计算结果知，在相同时间离散情况下二者结果相近。随时间步长Δt减小，两种伴随法灵敏度误差均逐渐减小，且相对误差与时间步长Δt的平方基本呈线性关系，即两种伴随法均具有二阶收敛速度，并与计算响应函数用Newmark-β法、梯形积分公式一致。

值得注意的是，虽先微分后离散伴随法存在一致性问题，但其灵敏度计算精度优于响应函数结果(图3、图4)，该现象为本算例特有，不具一般性。对本算例而言，一致性问题并未产生不良影响，反使灵敏度结果精度有一定程度提高。

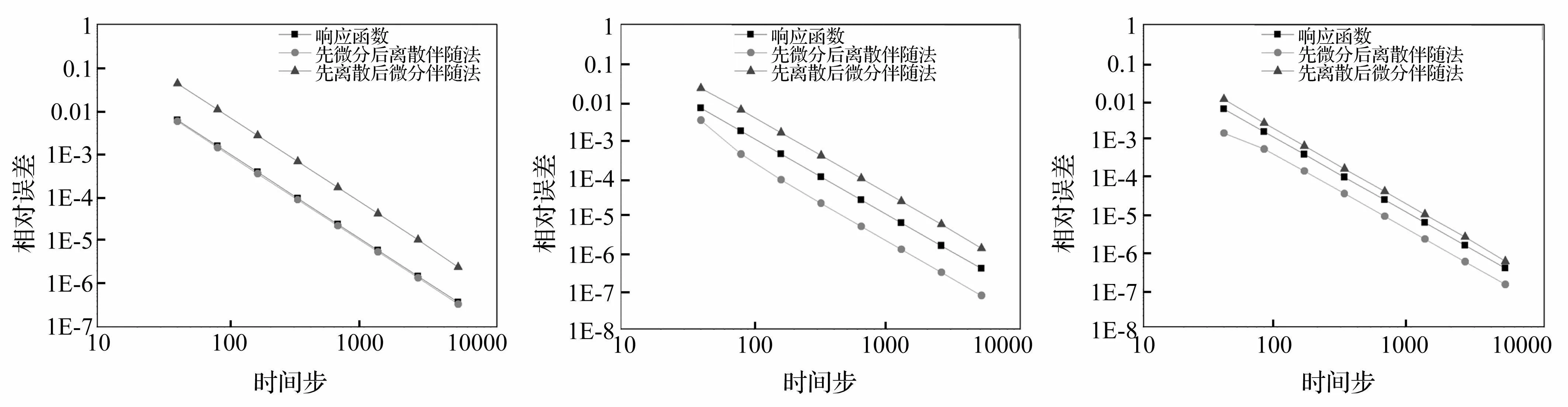
图2 单自由度振子响应函数Φ1及灵敏度相对误差Fig.2RelativeerrorsofresponsefunctionΦ1anditssensitivity图3 单自由度振子响应函数Φ2及灵敏度相对误差Fig.3RelativeerrorsofresponsefunctionΦ2anditssensitivity图4 单自由度振子响应函数Φ3及灵敏度相对误差Fig.4RelativeerrorsofresponsefunctionΦ3anditssensitivity

3.2三层剪切型结构

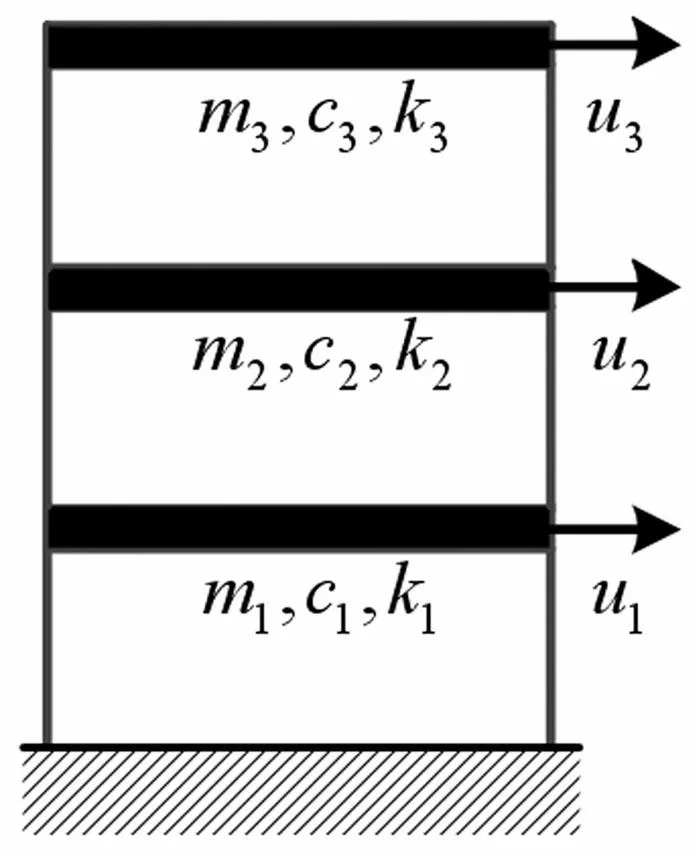
图5　三层剪切型结构 Fig.5 Three-storey shear structure

取两种形式的响应函数，即

考虑持时T=25T3，T3=0.607 5为第三阶自振周期。取不同离散时间步长Δt=T3/q，q为每个周期离散时间步数。采用两种伴随法分别计算响应函数对参数k2，k3的灵敏度，并与参考解比较，相对误差结果见图6～图9。动力响应及伴随向量计算仍用Newmark-β法，参数取γ=0.5，β=0.25。为获得准确可靠参考解，除采用较小时间步长外，用理查森(Richardson)外插法[14]计算参考解。

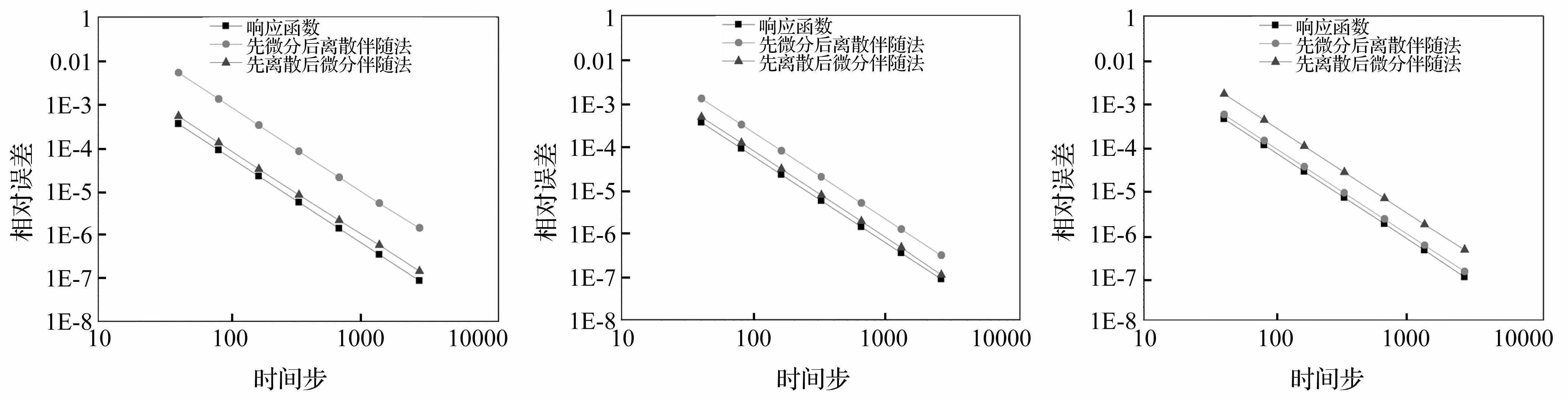
图6 三层剪切型结构Φ1及对k2灵敏度相对误差Fig.6RelativeerrorsofresponsefunctionΦ1anditssensitivitywithrespecttok2图7 三层剪切型结构Φ1及对k3灵敏度相对误差Fig.7RelativeerrorsofresponsefunctionΦ1anditssensitivitywithrespecttok3图8 三层剪切型结构Φ2及对k2灵敏度相对误差Fig.8RelativeerrorsofresponsefunctionΦ2anditssensitivitywithrespecttok2

在相同时间步长Δt下，由图6、图7看出，对响应函数Φ1，一致性误差导致先微分后离散伴随法灵敏度计算精度降低；而对响应函数Φ2，一致性误差可使灵敏度分析精度略有提高(图8)或降低(图9)。因此，虽一致性误差对灵敏度计算精度有影响，但影响作用不确定。另外，本算例灵敏度计算结果精度低于响应函数计算精度。随时间步数增加，两种伴随法计算精度均有提高，且与响应函数的计算具有相同二阶收敛速度。由此认为，时间离散误差仍为影响灵敏度计算精度的重要因素，一致性并不影响其计算收敛速度，该方法仍可靠。

图9　三层剪切型结构Φ 2及对k 3灵敏度相对误差 Fig.9 Relative errors of response function Φ 2 and its sensitivity with respect to k 3

4结论

通过研究结构动力响应灵敏度分析伴随法基本问题，包括算法的一致性、收敛速度及精度等，并由单、多自由度算例对比、讨论先微分后离散与先离散后微分两种伴随法的计算精度及收敛速度，结论如下：

(1)由于时域逐步积分方法所得动力响应解仅能保证在离散时间点处严格满足动力平衡方程，因此会导致先微分后离散伴随法出现一致性问题。

(2)时间离散误差是影响两种伴随法计算精度的重要因素，且两种方法二阶收敛速度相同。对先微分后离散伴随法，若能保证动力分析结果精度，一致性问题不会影响其可靠性。

(3)先微分后离散伴随法的理论推导及计算列式较简单，计算效率较高，虽存在一致性问题，但仍为较好的结构动力响应灵敏度分析方法。

参考文献

[1]陈太聪,韩大建,苏成. 参数灵敏度分析的神经网络方法及其工程应用[J]. 计算力学学报, 2004, 21(6): 752-756.

CHEN Tai-cong, HAN Da-jian, SU Cheng. Neural network method in parameter sensitivity analysis and its application in engineering [J]. Chinese Journal of Computational Mechanics, 2004, 21(6): 752-756.

[2]陈钢,赵国忠,顾元宪. 声场-结构耦合系统灵敏度分析及优化设计研究[J]. 振动与冲击, 2007, 26(4): 86-89.

CHEN Gang, ZHAO Guo-zhong, GU Yuan-xian. Sensitivity analysis and design optimization method for acoustic-structural coupled systems[J]. Journal of Vibration and Shock, 2007, 26(4): 86-89.

[3]毛玉明,郭杏林,赵岩,等. 基于灵敏度分析的结构动态载荷识别研究[J]. 振动与冲击, 2010, 29(10): 1-3.

MAO Yu-ming, GUO Xing-lin, ZHAO Yan, et al. Force identification based on sensitivity analysis method [J]. Journal of Vibration and Shock, 2010, 29(10): 1-3.

[4]赵杰,李峰,刘录. 基于有限元的超高压管线系统振动特性灵敏度分析 [J]. 振动与冲击, 2014, 33(10): 148-151.

ZHAO Jie, LI Feng, LIU Lu. Vibration characteristic sensitivity analysis based on finite element for ultra-high pressure pipeline systems[J].Journal of Vibration and Shock, 2014, 33(10): 148-151.

[5]Dahl J, Jensen J S, Sigmund O. Topology optimization for transient wave propagation problems in one dimension[J]. Structural and Multidisciplinary Optimization, 2008, 36:585-595.

[6]Kang Z, Zhang X P, Jiang S G,et al. On topology optimization of damping layer in shell structures under harmonic excitations[J]. Structural and Multidisciplinary Optimization, 2012, 46: 51-67.

[7]Le C, Bruns T E, Tortorelli D A. Material microstructure optimization for linear elastodynamic energy wave management[J]. Journal of the Mechanics and Physics of Solids,2012, 60: 351-378.

[8]Kang B S, Park G J, Arora J S. A review of optimization of structures subjected to transient loads[J]. Structural and Multidisciplinary Optimization, 2006, 31: 81-95.

[9]Keulen F V, Haftka R T, Kim N H. Review of options for structural design sensitivity analysis,part 1: linear systems [J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194: 3213-3243.

[10]Jensen J S, Nakshatrala P B,Tortorelli D A. On the consistency of adjoint sensitivity analysis for structural optimization of linear dynamic problems[J]. Structural and Multidisciplinary Optimization, 2014, 49(5): 831-837.

[11]Bathe K J. Finite element procedures[M]. Prentice-Hall, Englewood Cliffs, New Jersey, 1996.

[12]Kreyszig E. Advanced engineering mathematics (7th edn) [M]. New York:Wiley, 1993.

[13]苏成,徐瑞.非平稳激励下结构随机振动时域分析法[J]. 工程力学, 2010, 27(12): 77-83.

SU Cheng, XU Rui. Random vibration analysis of structures subjected to non-stationary excitations by time domain method [J]. Engineering Mechanics, 2010, 27(12): 77-83.

[14]Cook R D, Malkus D S, Plesha M E, et al. Concepts and applications of finite element analysis(4th edn)[M]. New York: Wiley,2000.

附录 A

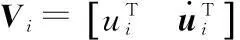
Vi=TVi-1+Q1ui-1+Q2ui

(A-1)

式中：

(A-2)

重复应用式(A-1)，可得第i时刻位移、速度响应计算式如下

(A-3)

式中： Ai,k为系数矩阵，可表示为

(A-4)

因此，各时刻点处的位移、速度响应可用对应时刻点及之前全部时刻点加速度显式表达成(A-3)形式。