基于SiC MEMS阵列的高精度微纳卫星编队保持

范林东,杨博,苗峻,龙军,刘旭辉

1.北京航空航天大学宇航学院,北京100191 2.北京控制工程研究所,北京100190

基于SiC MEMS阵列的高精度微纳卫星编队保持

范林东1,*,杨博1,苗峻1,龙军2,刘旭辉2

1.北京航空航天大学宇航学院,北京100191 2.北京控制工程研究所,北京100190

随着微纳卫星的发展,对它的控制保持问题亟需解决。传统的推进技术因推力精细度和推力输出相对粗糙,很难满足高精度的要求,为此,提出了用SiC MEMS微推力器阵列来解决微纳卫星的编队保持问题。由于阵列具有与传统发动机不同的特性,一般的控制算法很难用于该控制任务,文章提出了利用瞬时脉冲控制策略来实现编队保持。仿真结果表明,阵列用于微纳卫星近距离编队保持的位置精度可达3 mm,具有很高的应用价值。此外,为节省推力器,分析了单推力器装药量与控制器参数对能耗和精度的影响,结果表明当单推力器元冲量范围为8×10-6～20×10-6N·s时可以得到很好的控制效果,既能满足精度,又可以节约使用推力器。

编队保持;微机电系统;微推力器阵列;瞬时脉冲控制;参数优化;微纳卫星

对于微纳卫星的编队保持技术,由于受整星功耗、质量、体积等约束,国外只有少数卫星装备了冷气推进。冷气推进系统简单,已经通过飞行验证,但其可靠性易受电磁阀开关次数的影响,推力不可调[1-2],控制精度也不高,如加拿大CANX项目纳卫星的编队距离为50 m,其相对控制精度为1 m[3]。国内现有推进技术不能满足系统需求,已发射的微纳卫星均不具备推进系统[4]。

微机电系统(Micro-Electro-Mechanical System,MEMS)微推力器阵列是一种三明治结构的推进系统,利用微机电技术在同一块芯片上集成多个独立可寻址的微推力器,顶部为喷嘴层,中间为推进器存储单元,底部为电阻加热式点火层,通过组合的方式提供大小可变的冲量。早在20世纪90年代,TRW公司就设计了这种三明治结构,2000年Honeywell技术中心利用先进技术将26万余推力器集成到硬币大小的阵列上,此后,法国、韩国和日本的相关科研机构也设计了自己的微推力器阵列[5]。中国对该阵列的研制仅限于清华大学、国防科技大学等少数高校,集成度低,只制备了原理样机进行测试。且目前对MEMS阵列的研究都停留在系统本身的工艺研制,尚未进行卫星控制保持方面的应用研究。

基于目前微纳卫星编队保持技术的不足及MEMS推力器阵列可变的冲量和单个冲量精细的优点,提出了采用MEMS推力器阵列的微纳卫星的编队保持方法。由于推力器脉冲时间短,冲量离散,所以提出采用瞬时脉冲控制的方法进行选点控制,该方法可以有效地抑制随机大扰动。此外,由于采用了闭环实时反馈控制,还能获得较高的位置精度。本文以干涉测量卫星为背景[6],设计一个米量级的三角形微纳卫星编队,并对其进行编队保持。

1 编队保持任务描述

根据光学干涉成像系统测量原理可知,空间基线的精度直接影响着测量精度,要求编队卫星基本处于一种紧密的“刚性”连接。为了得到更高冗余度的干涉图像,宜采用多星编队的方式。

图1 主从星的相对运动Fig.1 Relative movement of center and follower

1.1 相对动力学建模

编队相对动力学建模目前分为两大类[7]:一类从相对状态出发,根据动力学分析得到相对运动方程;另一类从轨道要素出发,通过编队构形的空间几何关系得到相对运动方程。第二类方法虽然可以应用到非圆轨道的任务中,但它建立的方程非线性强,控制成本高,且轨道要素变化缓慢,不适于精确控制,因此对于高精度的近距离编队宜采用第一类方法建模。

图1中的坐标系Om-xyz为Hill坐标系,Om为主星原点,x轴沿主星质心和地心的连线背向地心,y轴在轨道平面内垂直于x轴指向主星运动方向,轨道系为右手直角坐标系。F为编队从星质心。

考虑到编队近距离和主星圆轨道的情形,从星在Hill坐标系中的相对运动方程可简化为Clohessy-Wiltshire方程模型[8]:

式中ωt为主星的轨道平均角速度;f为相对摄动加速度或控制加速度。

1.2 三角形编队设计

编队构形为等边三角形,三颗从星分别位于三角形的三个顶点,一颗主星位于三角形的中心。如图2所示,四颗卫星处于同平面以实现地面观测。构形尺度为1.5 m,为了利用自然力节约编队保持所需燃料,整个编队构形旋转角速度等同于自然力轨道下的旋转角速度,也就是主星的轨道角速度。

根据对C-W方程的分析,可知要想实现自然力下的空间圆编队,编队平面同Hill系的y-z面夹角应呈30°或150°[9-10]。以30°为例,设计编队,如图2所示,定义xcyczc为编队圆坐标系,在编队圆坐标系下从星的标准状态为

图2 编队构形设计Fig.2 Formation design

式中:r为编队圆半径;θ为编队从星的轨道转角,下标i为编队1、2、3号从星。则有:

式中:˙θi为主星轨道瞬时角速度,由主星的实时状态求解;T为离散步长。为构成三角形编队,θ1、θ2、θ3相位角相差2π/3。

由c系到Hill系的转换矩阵为Chc,得到三角形编队下从星的标准相对运动状态为:

1.3 编队保持需求

稳定的构形是编队卫星得以顺利完成任务的保证,但受模型误差、空间摄动力及随机干扰的存在,编队构形会逐渐发生变化,当编队卫星的实际状态偏离标称状态超过任务的误差容许限度时,就需要进行编队保持。

以1.5 m尺度的圆编队为例,用STK软件进行仿真计算,考虑模型误差、地球扁率、日月引力等作用下的编队飞行,得到一天的构形变化如图3所示(视角以主星运行方向为准)。结果表明,构形很快破坏,并在空间中发生了变形和旋转。

另外,从工程实现的角度来讲,由于构形尺寸较小,采用传统的二冲量修正方式显然不能完成需求,因此必须采用自主控制的方式完成编队保持。

图3 编队构形破坏分析Fig.3 Formation damage analysis

2 编队保持系统设计与仿真

根据编队构型设计,给定系统初始状态,利用相对导航系统提供导航信息反馈输入,同目标构形做偏差比较,得到偏差量作为控制策略的输入,提供给MEMS推力器阵列,最后对整个轨道保持系统做评估。整个系统进行模块化设计,主要包括以下四个模块:

1)仿真环境模拟:用数值积分的方式进行轨道递推,考虑地球扁率、大气阻力摄动,日月引力摄动和太阳光压摄动,以此来模拟实际飞行数据,为了获得精确的轨道数据,在STK软件环境下进行轨道递推。

2)推力器模型:考虑点火延迟时间、燃烧持续时间、推力输出形式等因素对阵列建模。

3)构形规划器:卫星编队展开后,顶层控制器还要根据任务的需要,实时生成编队卫星的标称轨迹,为构形的保持和变换提供目标和依据,构形规划器生成每一时刻的标准构形,其形式为相对运动状态量。

4)控制输入:由控制律解出的推力输入是主星轨道坐标系下的推力值,利用主星的轨道数据,求出主星的轨道坐标系和惯性坐标系的转换关系,将推力值转换成惯性系下的输入。

2.1 根据阵列特性建模

图4为阵列在卫星上的安装示意,控制对象为立方体卫星(Cube-Sat),六个面上各布置一片微推力器阵列。

阵列点火是通过逻辑寻址,加热底部的热电阻,从而将阵列中的某一推力器中的药柱点燃。SiC MEMS微推力器阵列有以下特点:

1)每个推力器相当于一个极小的火箭发动机,但它为一次性点火,喷完不可重复利用。

2)实飞中,单推力器输出元冲量不可控,但是可以在设计时通过调整装药量、燃烧室内径、喷嘴尺寸等改变。

3)可以通过组合点火产生大小可变的脉冲推力。

4)燃料消耗对卫星总体质量影响不大,单推力器药柱装药0.5～8μg,这样,即使上万个推力器全部燃烧,卫星总体质量减少很小。

5)由于推力器的制造成本较高,推力器个数受限,因此在使用中,更多要考虑的是节约推力器个数,而不是传统发动机的节约燃料。

6)随着工艺的提高,系统的集成度越来越高,如美国Honeywell技术中心研究的一种MEMS兆单元微型推进阵列由集成在3.3 cm× 3.3 cm硅片上的1 024×1 024个独立推进单元组成[11]。

下面,根据阵列特性进行推力建模,主要包括:输入指推力器个数需求;输出包括阵列的包络区间、单位最小推力、推力误差、点火延迟,燃烧时间和推力输出形式。图5给出了四种参考的推力输出形式。

控制系统的指令步长决定了平均分布模型中矩形的宽度,指令步长越短,冲量等效模型越接近于连续力模型。仿真中,综合考虑测量系统的采样时间、推力器点火时间、控制计算量和控制效果来选择指令步长。

由于MEMS微推力器阵列的单个推力器的冲量固定,所以每次的控制输入只能是元冲量的整数倍,对于矩形脉冲和三角形脉冲模型,还需要推力器点火延迟时间和燃烧时长。在控制仿真中,由于点火延迟(1.7 ms)和推力时间(15 ms)远小于控制步长,所以矩形脉冲模型和三角形脉冲模型足以反映实际推力器对控制系统的影响。

图4 SiC MEMS推力器阵列安装示意Fig.4 Installation of SiC MEMS thruster array

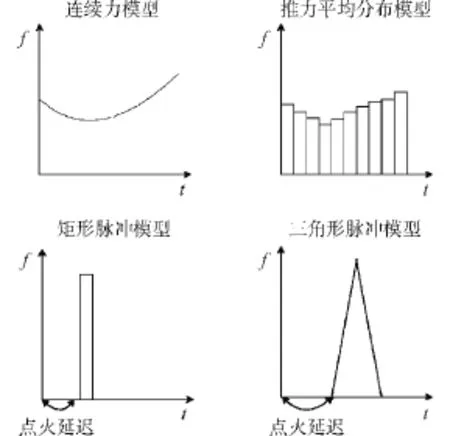
图5 不同的推力输出形式Fig.5 Thrust input-output form

2.2 基于阵列的闭环瞬时脉冲控制模式

在卫星的运行过程中,根据情况在标称轨道上等间隔地选取一些点,在这些点上采用脉冲推力达到轨控的目的。由于脉冲持续时间短,因此轨控过程可以认为只在某个时刻点发生。这种控制方式称为瞬时脉冲控制模式[12,13]。

阵列的输出为脉冲形式,所以该控制方式适合本任务研究。此外,由于其单位脉冲控制精细,具备完成高精度控制任务的优势,因此应考虑闭环反馈的控制。

控制系统利用星载计算机来实现,将式(3)按指令间隔T离散化:X(k+1)=eATX(k)+

式中:T为指令间隔时间。考虑阵列输出为脉冲形式,设tr为点火延迟时间,tc为燃烧持续时间,并替换积分中的τ,令t=(k+1)T-τ,式(7)可写成:

控制器给阵列的指令为点火个数,因此:

式中M(k)为指令给出的点火个数;Iu为单位推力器元冲量;m为卫星质量。

定义e=X-Xo,Xo为三编队从星的标称状态,详见式(6),则得到误差方程为

编队保持的目的是使控制后的卫星状态尽量与标称状态接近,同时消耗的推力器尽可能的少,以此为依据,选择最优指标函数:

式中:Q、S为对称半正定矩阵,是优化过程中误差和控制量的权值,它们的选取决定于对控制精度和推力器消耗的权衡。取反馈控制,对确定的Q,S最优控制有惟一解:

其中,P满足Riccati方程:P=Q+GT(P-1+HS-1HT)-1G。

2.3 数值仿真

本文仿真的立方体卫星尺寸10 cm×10 cm× 10 cm,质量1 kg,为了使仿真结果拟合实际,用STK软件进行仿真计算。仿真条件为:轨道历元为2015年1月1日0时0分0秒,坐标系为标准历元J2000.0的地心坐标系,取30×30阶次的WGS84_EGM96地球引力模型,大气阻尼系数Cd=2.2的Jacchia-Roberts大气模型,太阳光压选Cylindrical,卫星表面材料的吸光系数为1,考虑日月引力摄动,外推算法为HPOP,积分算法为RKF7(8)。编队从星初始误差选择不同量级(毫米级,厘米级,分米级),三颗从星的初始偏差分别为:e1=[0 0 0 0 0 0]、e2=[0 0-0.02 0 0 0]、e3=[0.5 0.7 0.9 0 0 0]。主星轨道选一低轨太阳同步轨道,卫星的初始轨道要素如表1所示。

系统离散步长为10 s,选定推力器元冲量Iu=10-5N·s,利用闭环瞬时脉冲控制进行编队保持,控制矩阵Q=I,S=10R×I,R参数选为8,控制过程如图6～图11所示。

表1 编队卫星的初始轨道要素Table 1 Initial orbital elements of formation satellites

图6 编队1号从星三轴偏差Fig.6 Three axis deviation of 1stfollow satellite

图7 编队1号从星推力器时序Fig.7 Thruster timing of 1stfollow satellite

图8 编队2号从星三轴偏差Fig.8 Three axis deviation of 2ndfollow satellite

图9 编队2号从星推力器时序Fig.9 Thruster timing of 2ndfollow satellite

图10 编队3号从星三轴偏差Fig.10 Three axis deviation of 3rdfollow satellite

图11 编队3号从星推力器时序Fig.11 Thruster timing of 3rdfollow satellite

图6～图11显示了编队从星的三轴位置误差的变化状态和阵列推力器各向需求时序。从仿真结果来看,本文设计的控制方法和控制律有效,基于阵列设计的控制器能达到很好的控制效果,有较好的动态响应和鲁棒性。即使分米级的初始误差,也能将其迅速地控制下来,动态响应时间低于500 s,可以满足空间应用,单时刻推力器消耗量不超过200,在兆单元推力器包络面内。

当控制达到稳定后,三颗编队从星在Hill系中的运动轨迹均为标准的圆形,位于同一平面内,各自相位差为120°,构成稳定的等边三角形,可以满足干涉测量的应用需求。

在稳态环境下(这部分编队保持控制力主要克服典型的空间摄动力),其位置误差及推力器需求见表2。

表2中控制精度为仿真1天三轴位置偏差序列的均方根误差,峰值指单时刻对推力器的最大需求量,单向及总和均为稳态下仿真一天的阵列推力器总和。为达到毫米精度的编队保持,单时刻点火一个,日消耗量低于150,阵列完全可以满足这个需求。另外,考虑y向推力需求明显低于其他两个方向,在卫星初设计之初,为节约成本,可以考虑减少阵列推力器个数。

表2 从星稳态精度和运行一天的推力器需求Table 2 Control precision of follow satellites and thrusters consumption per day

表3中的基线指两颗从星的直线距离,精度为该距离的实际值同标准值的偏差序列的均方根误差,由表3可知,控制稳态下基线的精度可以满足干涉测量需求。

表3 三角形编队基线精度Table 3 Baseline precision of triangle formation

3 参数优化

式(12)所描述的最优解是在参数矩阵已知的前提下得到的最优控制,因此,这个解仍有其局限性。理论上全局最优解在实际中很难实现,因为控制效果受到控制矩阵的选取、脉冲间隔的选取、控制点数,随机干扰及初始误差大小的影响,但是总可以通过优化找到效果较好的参数组合来满足控制需求。对于SiC MEMS微推力器阵列的控制来说,控制矩阵和推力器元冲量对控制效果的影响较大。下面通过数据仿真来寻找适合微纳卫星编队的参数组合。

通常在一个力学系统中,控制器的R参数取5～11,而现有的微推力阵列单推力器可装药为10-6～10-4N·s,下面通过数据仿真来寻找最合适的元冲量和R参数值。

图12为控制参数三维等高线,由图12(a)可知,控制精度是随着R参数和推力器冲量的增加而降低的,具有非常强的单调性。这是由于R越大,权衡精度的控制矩阵就相对减小,控制效果就越粗糙。而图12(b)中,推力器个数同时受R参数的影响和元冲量的影响。但是考虑到制备单推力器的成本较高,应当尽可能地节省推力器。仿真结果表明,当R参数值在8附近,而元冲量大于8×10-6N·s,可以得到更少的推力器需求量。

兼顾控制精度,将精度等高线与数量等高线画同一张图上,通过寻找区域交集得到使用最少推力器个数的参数,如图13所示。

图12 控制参数三维等高线Fig.12 3D contour map of control parameter

图13 参数寻优Fig.13 Parameter optimization

因此,R参数范围选在7.8～8.2附近,推力器元冲量范围为8×10-6～20×10-6N·s可以得到很好的控制效果。其位置精度高于3 mm,而单日推力的消耗低于150个。对于256×256的推力器阵列,考虑推力器过卫星质心对称点火,可以保证至少3年的编队运行寿命。

5 结束语

本文研究了基于SiC MEMS微推力器阵列的微纳卫星编队保持问题:设计了适用于光学干涉测量的三角形卫星编队,对阵列进行特性分析和建立模型,并针对其输出特点提出利用闭环瞬时脉冲控制策略进行编队保持。结果表明,所设计的控制器实现了标称状态的跟踪,验证了控制方法的有效性;同时表明该阵列可以满足近距离微纳卫星的高精度编队,可以解决传统推进技术在微纳卫星上应用受限的问题,为阵列的编队保持应用提供了仿真试验支持,证明这种新型推力器在微纳卫星上具有广阔的应用前景。对于阵列而言,推力器成本较高,因此通过参数寻优来设计控制器和阵列,可以大限度地延长卫星编队运行寿命。另外需要指出的是,为了节省推力器,参数优化过程中还牺牲了一些精度,而且阵列很难承受得起克服大扰动力的消耗,因此下一步拟研究传统小推力器(如电推进,冷气推进)与阵列组合控制,有望实现寿命更长、精度更高的编队控制。

References)

[1] 张召才,朱鲁青.2014年国外小卫星回顾[J].国际太空,2015(2):63-70.

[2] 林来兴.现代小卫星的微推进系统[J].航天器工程, 2010,19(6):13-20. LIN LAIXING.Micro-propulsion system for modern small satellites[J].Spacecraft Engineering,2010,19(6):13-20 (in chinese).

[3] 李军予,伍保峰,张晓敏.立方体纳卫星的发展及其启示[J].航天器工程,2012,21(3):80-87. LI J Y,WU B F,ZHANG X M.Development of cubesat and its enlightenment[J].Spacecraft Engineering, 2012,21(3):80-87(in chinese).

[4] 高辰.中国航天开展微纳卫星推进系统基础技术研究[EB/ OL].[2014-04-03].http:∥www.chinanews.com/mil/ 2014/04-03/6027005.shtml.

[5] 徐超.MEMS固体微推进器的设计与制备[D].长沙:国防科技大学,2006. XU C.Design and fabrication of MEMS based solid propellant micro thruster[D].Changsha:National University of Defense Technology,2006(in chinese).

[6] CHIRS SABOL,RICH BURNS,CRAIG A MCLAUGHLIN,et al.Satellite formation flying design and evolution[J].Journal of Spacecraft and Rockets,2001,38(2):270-278.

[7] 孟云鹤.航天器编队飞行导论[M].北京:国防工业出版社,2014:10-32. MENG Y H.Introduction to spacecraft formation flying[M].Beijing:National Defense Industry Press, 2014:10-32(in chinese).

[8] 张世杰,段广仁.分布式卫星编队飞行队形保持协同控制[J].宇航学报,2011,32(10):2140-2145(in chinese). ZHANG S J,DUAN G R.Cooperative control for distributed satellite formation keeping[J].Journal of Astronautics,2011,32(10):2140-2145(in chinese).

[9] 肖业伦,张晓敏.编队飞行卫星群的轨道动力学特性与构型设计[J].宇航学报,2001,22(4):7-12. XIAO Y L,ZHANG X M.Orbital dynamical characteristics and configuration design of formation flying satellites[J].Journal of Astronautics,2001,22 (4):7-12(in chinese).

[10] TERRY ALFRIEND,SRINIVAS VADALI,PINI GURFIL,et al.Spacecraft formation flying dynamics,control and navigation[M].UK:Elsevier Astrodynamics Series,2010:13-59.

[11] YOUNGNER D W,LU S T,CHOUEIRI E,et al. MEMS mega-pixel micro-thruster arrays for small satellite stationkeeping[R].North Logan(USA): AIAA,2000.

[12] BREAKWELL J V,KAMEL A A,RATNER M J. Station-keeping for a translunar communication station [J].Celestial Mechanics,1974,10(3):357-373.

[13] DREW R.JONES,HANSPETER SCHAUB.Collinear three-craft coulomb formation stability analysis and control[J].Journal of Guidance,Control,and Dynamics,2014,37(1):224-232.

(编辑:车晓玲)

High precision micro-nano satellite formation keeping based on SiC MEMS micro thruster array

FAN Lindong1,*,YANG Bo1,MIAO Jun1,LONG Jun2,LIU Xuhui2
1.SchoolofAstronautics,BeihangUniversity,Beijing100191,China 2.BeijingInstituteofControlEngineering,Beijing100190,China

With the development of the micro/nano satellites,the problem of the stationcontrol needs to be solved.The traditional propulsion technology can't meet the requirements of high precision.Therefore,the SiC MEMS Micro thruster array was proposed for the formation keeping of the micro/nano satellites.Considering the different characteristics of the array from the traditional thruster,the input and output model was established and the instantaneous pulse control strategy was presented to keep the formation.The simulation results show that the array can be applied to the near distance formation of micro/nanosatellites,and it has a high position accuracy of 3 mm.In addition,the thrusters' consumption and control precision influenced by the single thruster charge and controller parameters were analyzed.When the impulse of the single thruster range is 8×10-6～20× 10-6N·s,it can get good control.

satellite formation keeping;MEMS;micro thruster;instantaneous pulse control; parameter optimization;micro-nano satellite

P185.18

:A

10.16708/j.cnki.1000-758X.2016.0002

2015-07-02;

:2015-10-16;录用日期:2015-09-28;< class="emphasis_bold">网络出版时间

时间:2016-04-19 14:54:43

http:∥www.cnki.net/kcms/detail/11.1859.V.20160419.1454.003.html

*

:范林东(1988-),男,硕士研究生,fanlindong@buaa.edu.cn,主要研究方向为卫星导航制导与控制

范林东,杨博,苗峻,等.基于SiCMEMS阵列的高精度微纳卫星编队保持[J].中国空间科学技术,2016,36(2): 37-45.FANLD,YANGB,MIAOJ,etal.Highprecisionmicro-nanosatelliteformationkeepingbasedonSiCMEMS microthrusterarray[J].ChineseSpaceScienceandTechnology,2016,36(2):37-45(inChinese).

http:∥zgkj.cast.cn