概念定义灵活用 转化运算促解题——高三解析几何复习解题教学的几点思考
杨静(杭州余杭实验中学,浙江 杭州 311100)
概念定义灵活用 转化运算促解题——高三解析几何复习解题教学的几点思考
杨静
(杭州余杭实验中学,浙江 杭州 311100)
解析几何教学是高中数学教学的重点内容,同时对学生来说也是难点所在,从高考中解析几何的地位来看,其所占的分值也相对较大.从知识方面来看,高考命题常常立足于圆锥曲线的背景、定义以及问题解决过程中的几何转化等方面来设计;从能力方面来看,椭圆与双曲线无论在概念、方程以及几何性质上都具有较强的相似性,因此,其研究方式主要集中在类比迁移及差异分析等思维特质上,此外,对抛物线问题的考查,常常结合抛物线的定义及其几何性质进行灵活转化与应用,这些方面对学生而言都提出了较强的挑战性.从考查的核心指向(体现学科特点)来看,高考中对解析几何的考查必然结合了数形结合、化归转化等数学思想方法,同时结合了较为复杂的运算,对学生的数学思维和运算能力也提出了更高的要求。
作为高三复习解题教学,只有理解背景,立足定义,注重转化,优化运算从这四个方面进行教学指导,才能让学生学好解析几何,提升解题的能力,同时教师的复习课堂也才能更有效。
一、理解背景,曲线类型明辨析
教材中对圆锥曲线的背景在章头图中有明确的探索与演示:“将两个共点的圆锥放在一起,用平行于底面的平面去截,则得到的曲线是圆;将其稍作倾斜,得到的曲线是椭圆;若继续倾斜,当截面与母线之一平行时,则得到抛物线;再继续将平面转起,则平面与上下两个共点圆锥均相交,此时的曲线是双曲线.这是圆锥曲线名称的由来,其起源自古希腊数学家对于圆锥的研究得到的名称,一直沿用至今.教材的“探索与发现”栏目中对圆锥的截口曲线为什么是椭圆更有进一步的推理与设问.
在高三复习教学中,对这一章的章头图及“探索与发现”栏目中内容有必要仔细分析,让学生理解解析几何的概念,会在概念的指导下在截面与圆锥的母线的关系中生成圆锥曲线.
结论:用一个不过圆锥面顶点的平面去截一个圆锥面,当平面圆锥的轴所成的角θ与圆锥母线与轴所成角α大小关系不同时,交线的不同情况如图所示:
例1.(2015年浙江省高考数学文科第7题)如图,斜线段AB与平面α所成的角为60°,B为斜足,平面上的动点P满足∠PAB=30°,则点P的轨迹是( )
A.直线 B.抛物线 C.椭圆 D.双曲线的一支
分析:解决本题的关键是要学生有立体几何的模型——当动直线与定直线成角为定角时,动直线即为以定直线为轴的圆锥的母线,有了这个圆锥面的模型后再结合解析几何的生成概念就不难得出答案了。
解:由AP与AB成定角为30°,可知AP是以AB为轴的α=30°的圆锥的母线,又AB与平面α成角为60°,即θ=60°可知α< θ <90°,因此交线为椭圆。
由此我们可以进一步得到:
当AB与平面α成角为θ=30°时,交线为抛物线;
当AB与平面α成角0≤θ< 30°时,交线为双曲线.
在实际的教学中,解析几何的复习往往更多关注的是解题的重复训练和反复操作,这也在一定程度上体现了教师自身对这块内容理解的不够到位,把反复训练当成是复习的全部显然不利于学生对概念的理解和解题能力的提升,学生在遇到这样的考题时只能是望而却步。
笔者认为,在圆锥曲线的复习教学中,只有让学生在动手操作中进行模型识别,在探究与推理中深刻理解圆锥曲线的背景,把对于圆锥曲线概念的背景、本质特征、内涵与外延的理解放在首位,才能切实帮助学生对圆锥曲线概念的同化,真正体会与梳理在问题解决过程中的方法,促进学生提升在问题解决过程中的思维和能力,实现认知图式的扩张.
二、立足定义,数形结合促解题
解析几何是在直角坐标系的背景下用代数方法研究几何性质的典范,是数形结合思想的典型,但如果用纯代数的方法进行研究,有时运算复杂,技巧较多,如果能利用图形先作几何量化的分析,数形结合的处理问题,能起到事半功倍的效果。
高三解析几何复习解题教学必须立足圆锥曲线的定义,椭圆、双曲线注重焦点三角形的灵活应用,抛物线关注焦点弦的基本性质等基本知识点,这些基本知识和基本性质是落实基础的关键。
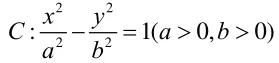
本例中用了两次定义求得a,同时又对两个焦点三角形的公共角应用余弦定理得到关于c的方程,从而求得c,进一步得到e,焦点三角形的仔细观察及余弦定理的两次应用是解决这个题目的关键。
笔者认为,高三的复习解题教学必须从基本定义及性质入手,善于观察图像的特点,用数形结合的思想引领解题,灵活应用定义,这样才能夯实基础,提升对此类题目的本质理解,有利于解题能力的提升。
三、注重转化,思想方法齐渗透
在解决一些综合性较强的解析几何问题时,学生的困难往往是题目中的几何条件不能准确地转化为代数形式,导致问题无法解决。对于几何条件的准确转化其实质是数学思想方法的体现。
在高三复习解题教学中,数学思想方法的教学应逐步成为解析几何重点与核心,因此,只有在解题复习教学中逐步渗透数学思想方法,对解析几何问题结合化归转化,数学结合,方程函数等数学思想方法的教学,才能使学生对其理解透彻。
例3.(2015年浙江省高考数学理科第5题)如图,设抛物线y2=4 x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则ΔBCF与ΔACF的面积之比( )
分析:解好本题的关键是降维和转化的数学思想——把ΔBCF 与ΔACF的面积之比转化为弦长BC与AC之比,再用抛物线的定义进行求解。
解:由A, B , C三点共线,及抛物线的定义
本题以直线与抛物线的位置关系为背景,考查转化与化归及数形结合的数学思想方法,题目表述十分简洁,但对学生的转化与化归能力是又一定的要求的,这样的解题如果没有平时思想方法的不断渗透,学生在解题过程中必然会碰到困难。
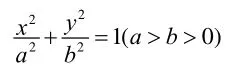
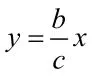
这是一道求椭圆离心率的题目,命题与浙江省的命题风格“条件简洁、问题清楚”相一致,但考生普遍反映“入手容易,运算困难”,其实只要对题目的题意理解清楚,等价转化到位,结合圆锥曲线的定义,题目的运算量是不大的,上述的这种解法,渗透了等价转化,数形结合等数学思想方法,自然、流畅,计算简洁。
笔者认为,在高三解析几何复习教学中,只有不断渗透数学思想方法,让学生能准确理解题目的含义,灵活转化题目的条件,再结合圆锥曲线的定义及相关基本性质,才能灵活解题,提高复习的效率。
四、优化运算,整合突破提能力
解析几何的解题必然结合着较为复杂的运算,这也是学生感觉解析几何问题解决较为困难的一个重要方面,但这样的运算又无法回避,这就需要在平时多加以训练.
在高三复习教学中,在运算训练上可以形成模块化的训练,如直线与曲线方程的联立,弦长公式,面积求法,分式函数最值的求法等.同时还要注重在运算过程中与其他知识的整合与衔接,如与函数结合的最值求法,与方程结合的韦达定理应用等,这些模块的运算训练中较少的涉及解题思维问题,要求学生准确快速的运算,通过这样的运算训练学生在复习时才能解题效率,在高考时才会有更足的底气。
分析:本题的转化是熟悉的,直接把弦长比转化为坐标比,解好本题的关键在于运算,当“设而不求”运算有困难时,不妨“设而求之”。
这种解法的实质是消元的思想,直接把t转化为了k的函数进一步求解。
解法3看似繁琐,对于学生来说似乎更加自然,数据的处理也相对容易,但一般学生不会想到去尝试,他不符合我们一般的解析几何的解题经验,在“设而不求”作为解析几何运算中的重要方法的前提下,运用韦达定理运用有困难时不妨“设而求之”。
笔者认为,高三解析几何复习解题教学的课堂,教师要舍得花时间让学生去算,从而暴露学生的运算思维,教师也要舍得花时间进行板演,给学生作必要的运算示范,同时在运算过程中要注重整合,如分式函数的最值处理方法,方程韦达定理的灵活处理等,让学生能在运算过程中去领悟这种思想方法,从而整合突破,做一个会一类,形成高效的复习.
总之,高三解析几何的解题复习教学需要每一位高三教师必须提高解题复习教学的有效性.作为高三复习教学的主导者,让我们转变观念,摒弃通过大量练习,使学生形成解题思维定式的复习方法.通过对解析几何的理解背景,立足定义,注重转化,优化运算四个方面入手,真正提升学生的解题能力。
参考文献:
[1]谢舒.浅析解析几何教学的三重境界[J].中学数学,2015(12):53-55。.
[2]李健.从条件转化看解析几何教学中思想方法的渗透[J].中学数学,2014(5):46-48。
中图分类号:G633.63
文献标识码:A
文章编号:1671-864X(2016)01-0274-03

