基于最大熵原理的径流预报误差分布规律研究

何 洋，纪昌明，田开华，张验科，李传刚(.华北电力大学可再生能源学院，北京 006；.雅砻江流域水电开发有限公司，成都 60056)

0 引 言

随着信息与预报技术的发展，径流预报的预报方法逐渐丰富，预报精度也逐步提高。但由于流域径流受水文、下垫面、人类活动及水文模型等因素的影响，径流预报结果的不确定性十分明显，预报误差不可避免[1]。

对径流预报误差统计特性的研究包括对其分布规律和误差出现不确定度的研究两个方面。目前，大多数文献主要利用参数估计[2]、非参数估计[3]和统计图形[4]等方法分析洪水预报误差的分布特性，通常认为其预报误差服从或近似服从正态、对数正态和Laplace等分布形式。但这些方法均无法直接推导出洪水预报误差的先验分布，带有明显的主观性。最大熵法能依据有限的历史径流序列，推求一种最小有偏概率分布，并与直接概率方法得到的结果相一致，其结果具有无偏性和客观性，因而被广泛应用于水科学领域[5]。文献[6]建立了洪水总量预报误差分布的极大熵模型，分析不同预报误差的分布规律，结果表明通过极大熵模型能求得一个与已知预报误差序列拟合较好的分布；文献[7]采用最大熵原理，计算了我国湿润和半湿润地区部分典型水库的净雨、洪峰流量和峰现时间预报相对误差的概率密度函数，结果表明最大熵法研究洪水预报误差分布是可行的；文献[8]详细阐明了推求洪水预报误差分布的问题本质及最大熵原理的适用性分析，结果表明最大熵原理在推求洪水预报误差分布时是合理可行的，且洪水预报作为径流预报的一部分，因而它也间接证明了径流预报同样适用最大熵原理。但上述文献均仅推求径流预报整个误差系列的分布规律，且未能在此基础上以概率形式定量描述径流预报的不确定性，其实用性不高。为此，本文以官地水库为研究对象，以其不同预见期的历史径流预报资料为数据基础，应用最大熵原理，建立径流预报误差的最大熵模型，开展径流预报误差分布规律的研究，同时考虑流域径流年内丰枯变化对其分布规律的影响，对整个径流的误差序列进行分时期研究，从而更好地掌握径流预报误差的分布规律。

1 径流预报误差分布的最大熵模型

为了解决不确定性问题，科学家E T Jaynes[9]在信息论中引入最大熵原理，它是根据样本信息对某个未知分布做出推断的一种方法。其准则是在以不完整信息作为依据进行推断时，承认已知事物，且不对未知事物做任何假设，在所有的可行解中选择熵最大的一个解，其解是唯一的，且同为指数函数的形式。

1.1 最大熵模型

设x为径流预报相对误差(以下简称“误差”)系列：

(1)

其概率密度函数为f(x)，建立最大熵模型[10]：

(4)

x≥a或x≤b

(5)

其中x=G(x1,x2,…,xn)

(6)

式中：n为径流预报的系列长度；qi、Qi分别为径流系列的预测值和实测值；Ω为径流预报误差x所在的集合；m为矩的阶数；mi表示第i阶原点矩；a、b为保证x有意义的误差上下限。

该模型表示在满足已知信息约束下，以熵最大为准则求得径流预报误差的概率密度函数。

1.2 模型求解

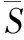
(7)

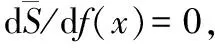
(8)

或

(9)

式(9)是基于最大熵原理得到的概率密度函数的解析形式。将其代入式(3)中解得：

(10)

或

(11)

将式(10)对λi微分，并考虑到式(4)和式(9)，可得：

(12)

为求解各个λi，可建立一个联立方程组，将式(11)对λi微分，可得：

(13)

由式(12)和式(13)可得：

(14)

通过式(14)可求解λ1,λ2,…,λm，代入式(11)求出λ0。为了便于数值求解，将式(14)改为：

(15)

式中：Ri为残差，可用数值计算方法使其趋于零，用非线性规划求这些残差平方核定最小值，就可得到问题的解：

(16)

为了用非线性规划求解在算法中还要假定有一个初始点，文献[10]提供了四种不同的确定初始点的方法，分别为假设分布是正态、假设分布是均匀、综合协调法和逐步起点法，可由算法按给定的顺序依次试用。当R<ε(ε为规定的允许误差)或所有的|Rj|<ε时认为上式收敛，从而求解出λ0,λ1,λ2,…,λm，最后求出最大熵概率密度函数的唯一解析表达式。其流程图如图1。

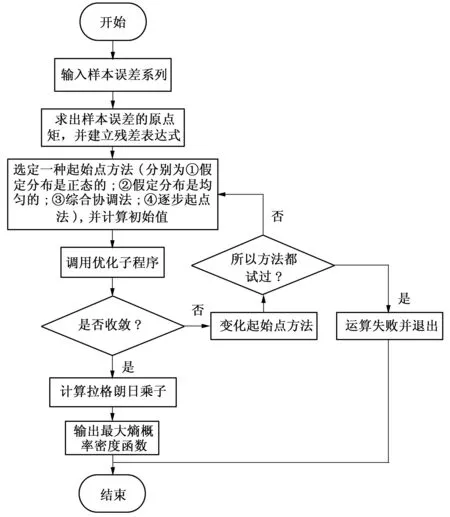
图1 求解最大熵概率密度函数流程图Fig.1 Flow chart of maximum entropy probability density function

2 实例应用

2.1 水库概况

官地水库是雅砻江卡拉至江口河段水电规划五级开发方式的第3个梯级电站。水库正常蓄水位1 330 m，正常蓄水位对应库容7.292亿m3，最大调节库容1.232 亿m3，为日调节水库，总装机容量240万kW，设计多年平均发电量为110.160 亿kWh。该水库位于雅砻江流域下游，流域降水具有明显的季节性变化，径流的年际、年内丰枯变化与降雨季节变化趋势一致，按径流量及补给来源可大致分为：汛期7-9月、汛枯过渡期10月、枯汛过渡期5月和6月、枯水期11月-翌年4月[11]，具体划分结果见表1。目前，官地水库在当日早8∶00和晚8∶00分别进行一次径流预报，预见期分别为6、12、18、24 h，利用不同预见期的预报成果，制定明日发电计划。因此，研究不同预见期的预报误差分布规律能促进发电计划编制的合理性。本文选取该水库2012年3月-2014年12月不同预见期的新安江模型径流预报成果进行误差分布研究。不同预见期的径流预报相对误差的统计描述量见表2，其中确定性系数表示径流预报过程的离散程度，计算结果表明其预报精度均达到甲等(大于0.9)，符合规定。

表1 官地水库径流序列时期划分表Tab.1 Guandi reservoir runoff period division table

表2 不同预见期的径流预报相对误差的统计描述量Tab.2 Statistical description of relative error of runoff forecasting for different forecast periods

2.2 径流预报误差分布的计算及分析

以官地水库整个时期的径流系列为例。最大熵模型计算径流预报误差分布规律时，样本估计总体统计参数的3阶以上的原点矩与理论值偏差较多，其抽样误差较大，因此仅采用序列的前3阶原点矩建立约束条件，计算其整个时期不同预见期的径流预报相对误差的3阶原点矩，见表3；建立官地水库径流预报误差分布的最大熵模型，经验证可利用逐步起点法假定初始点，将1.2[μ-5σ，μ+5σ]作为误差域[12]，并采用非线性规划求解函数推求式中的Lagrange乘子，结果见表4。

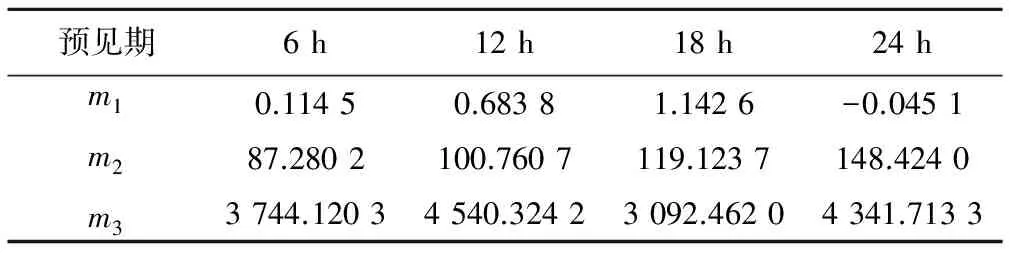
表3 不同预见期的径流预报误差原点矩Tab.3 The origin moment of runoff forecast errors in different forecast periods

表4 不同预见期的径流预报误差Lagrange乘子Tab.4 Lagrange multiplier of Runoff forecasting error of different forecast period

由表4可确定官地水库不同预见期的径流预报误差的最大熵概率密度函数，函数式如下(设x1、x2、x3、x4分别表示预见期为6、12、18、24 h的径流预报相对误差序列)，并绘制不同预见期径流预报误差的最大熵分布曲线，同时给出其理论正态分布曲线和样本直方图作为对比，见图2。

f(x1)=exp(-2.982 6-0.020 9x1-0.008 2x21+

1.035 3×10-4x31),x1∈[-55.9,56.2]

(17)

f(x2)=exp(-3.008 0-0.016 0x2-0.007 9x22+

1.154 0×10-4x32),x2∈[-59.3,60.9]

(18)

f(x3)=exp(-3.158 2-0.005 3x3-0.005 7x23+

5.553 7×10-6x33),x3∈[-63.8,66.5]

(19)

f(x4)=exp(-3.193 9-0.006 1x4-0.005 3x24+

1.597 9×10-6x34),x4∈[-73.2,73.1]

(20)

图2 不同预见期的最大熵分布曲线、正态分布曲线和样本直方图的对比图Fig.2 Comparison diagram of the maximum entropy distribution curves and normal distribution curves and sample histogram in different forecast period

由图2可看出，对于不同的预见期，径流预报误差的样本直方图的形状均呈中间高，两边低，左右基本对称，初步表明径流预报误差系列呈正态分布；最大熵曲线与理论正态分布曲线基本吻合，两曲线形状、走势相差不大，表明得到的最大熵曲线是比较合理的；相比于理论正态曲线，最大熵曲线的形状更“高瘦”，预报误差集中度更高，曲线最大概率值更大，且更接近样本直方图的最大概率值，这符合熵集中原理，即预报误差的绝大部分可能状态都集中在最大熵状态附近；最大熵曲线与样本直接图一样其误差均有上下限，而理论正态曲线的积分区间为±∞。因此，相比于理论正态曲线，最大熵曲线拟合效果更好，更符合实际情况。

考虑流域径流年内丰枯变化对其预报误差分布的影响，分别计算官地水库枯水期、汛期和过渡期的6、12、18和24 h的径流预报误差的最大熵概率密度函数，并绘制不同时期及不同预见期的径流预报误差最大熵曲线，分别见图3和图4。

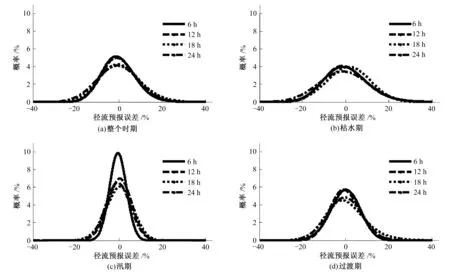
图3 不同时期的最大熵曲线对比图Fig.3 The contrast diagram of Maximum entropy distribution curves of different period

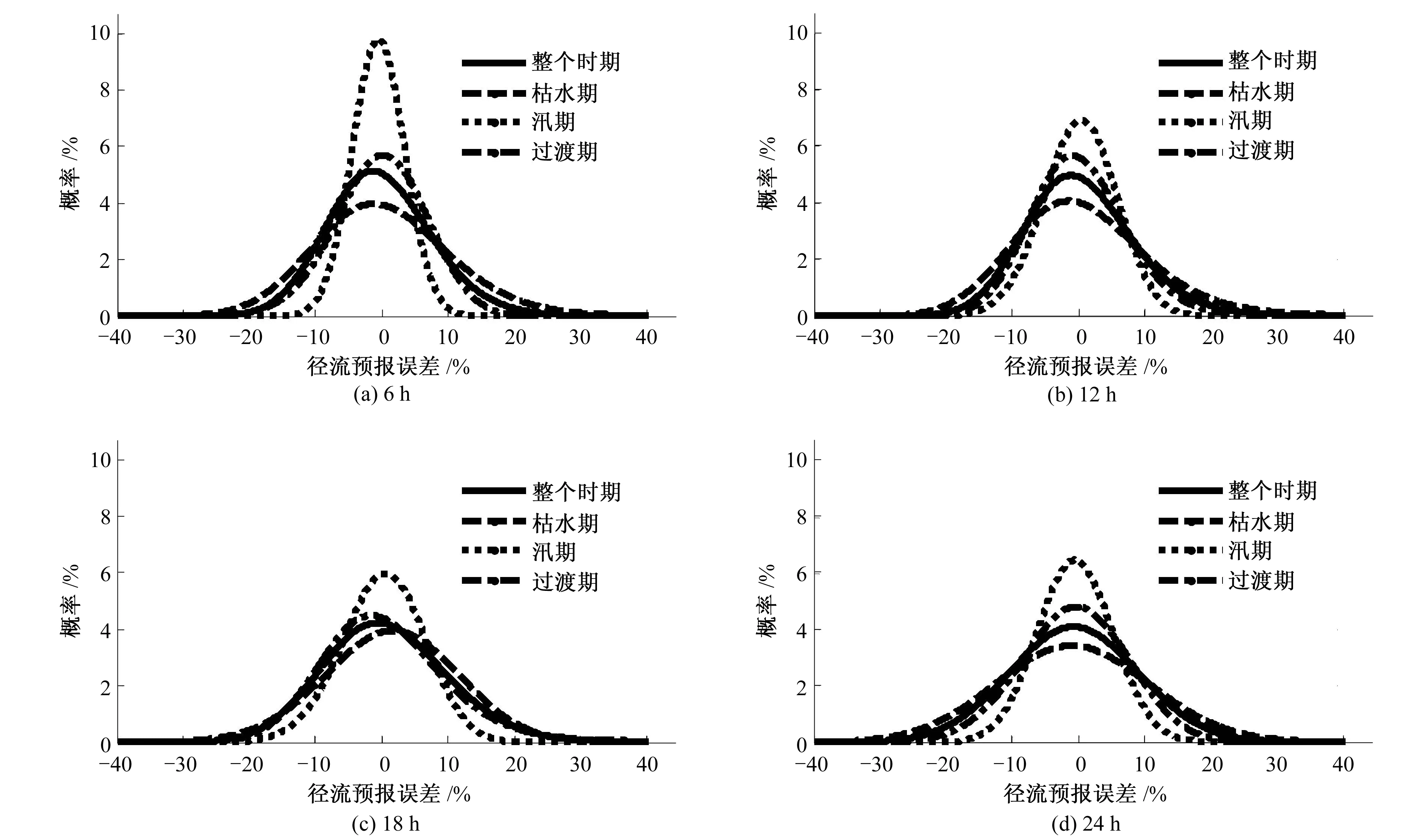
图4 不同预见期的最大熵曲线对比图Fig.4 The contrast diagram of Maximum entropy distribution curves of different forecast periods

(1)由图3可看出，对于不同时期，随着预见期的增加，其最大熵曲线的形状基本上均由“高瘦型”逐渐变为“矮胖型”，曲线的最大概率值逐渐降低，均值附近的误差分布集中度逐渐降低，表明对于同一时期做出的径流预报，随着预见期增加，预报精度降低，其不确定性增加。表5列出了不同时期、不同预见期及不同置信区间预报误差的置信度。由表5可知，当预见期为12、18和24 h时，相比于整个时期、枯水期或过渡期，汛期的预报误差在相应置信区间内的置信度差异较小，与预见期为6 h相应的置信度差异较大，但从区间③开始，随着置信区间的加大，各个预见期置信度的增加幅度均比较缓慢，表明汛期各个预见期的预报误差分布均比较集中，预报精度较高。这主要是因为受降水年内分配不均匀的影响，相比于枯水期和过渡期，汛期的径流大且波动性强，随着预见期的增加，径流预报值的随机性更强，变化幅度更大，使其最大熵曲线变化更大。但就整体上而言，不同时期、不同预见期预报误差位于[-20%,20%]置信区间的置信度基本达到0.95左右(仅24 h预见期的枯水期置信度最低为0.914)，预报精度均达到甲等。

(2)由图4和表5可看出，对于不同预见期，其最大熵曲线基本上是汛期最“高瘦”、过渡期次之、整个时期再次之、枯水期最“矮胖”，对应地，其预报精度由高到低依次为汛期、过渡期、整个时期和枯水期。当预见期为6 h时，相应的预报误差位于区间③的置信度分别为0.958、0.837、0.796和0.677，其差异较大，汛期预报误差的置信度远高于其他时期，且置信区间越大，其差异越小。这主要是由于受防洪需要，虽然汛期流量大且波动性强，但现有的新安江模型在多年的实际预报工作中已能较好地发掘该时期的径流规律，使其预报精度高于其他时期；过渡期径流主要受降雨和河槽蓄水补给等影响，其流量波动较强，造成该时期预报精度较低，预报不确定性较大；枯水期由于其流量极小，预报产生的较小差异也将造成其相对误差值的较大变化，使该时期的预报精度最低，不确定性最大。

表5 不同时期、不同预见期及不同置信区间预报误差的置信度Tab.5 The confidence of prediction error of different period, different forecast period and different confidence interval

注：置信区间的单位为“%”。

(3)对整个时期而言，尽管预见期不同，其最大熵曲线总是介于枯水期、汛期和过渡期之间。整个时期预报的不确定性是各个时期综合作用的结果，尽管汛期预报的不确定性很小，但由于枯水期预报不确定性较大，从而增加了整体预报结果的不确定性。因此，在进行径流预报工作时，应充分考虑不同时期的预报误差分布规律对其预报结果的影响，从而提高径流预报的精度。

2.3 适用性判断

为了评判最大熵分布在官地水库径流预报误差分布研究中的适用性，本文以整个径流序列为例，将最大熵曲线与理论正态曲线的拟合效果进行对比分析，分别采用判定系数(coefficient of determination，ηCOD)和均方根误差(root mean square error，εRMSE)[13]以量化各曲线的拟合优度，并分别计算不同预见期的最大熵曲线和理论正态曲线的熵值，计算结果见表6。计算公式分别入下：

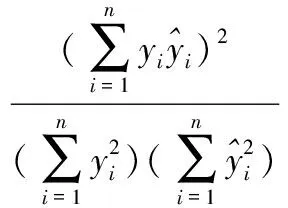
(21)

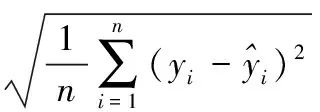
(22)

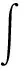
(23)

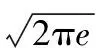
(24)

由表6可知，对于整个时期的径流序列，预见期分别为6、12、18、24 h时，最大熵的熵值均比正态分布的小，表明由最大熵法确定的误差分布曲线的不确定性更小；最大熵法的判定系数均比正态分布的大，而均方根误差均比正态分布的小，表明最大熵法在拟合径流预报误差时效果更好，各个时期的最大熵曲线适用性判断结果类似。可见，最大熵法作为一种对未知分布进行推断的方法，其不确定性小，拟合效果比标准正态分布的更好，说明该方法在对径流预报相对误差分布的研究是合理可行的。

表6 最大熵分布和正态分布的适用性判断表Tab.6 The applicability judgment table of maximum entropy distribution and normal distribution

3 结 语

通过最大熵模型对官地水库2012年3月-2014年12月不同预见期的入库径流预报误差系列进行研究，结果表明最大熵法在拟合径流预报误差分布时，其熵值最小，拟合效果更好，适用性也更强；同时，考虑流域径流年内的丰枯变化，分别计算了不同预见期的整个时期、枯水期、汛期和过渡期的最大熵概率密度函数及其分布曲线，并给出不同置信区间下的置信度，其中预报误差位于[-20%,20%]置信区间的置信度基本达到0.95以上，预报精度达到甲等，预报精度由高到低依次为汛期、过渡期、整个时期和枯水期，且各个时期预报误差的不确定性均随着预见期的增加而增大。但由于官地水库现有的径流系列较短，本文仅考虑按时期对径流系列进行划分，待径流系列的逐步延长，可考虑按流量级别对其划分，求出不同流量级别下的径流预报误差最大熵概率密度函数，探索不同流量级别的径流预报误差分布规律，从而更好的掌握径流预报误差的分布规律，更加合理的编制其发电计划。

□

[1] 朱星明，安 波，王成明，等.水库流域入库洪水预报误差分析[J].水文，1997,(6)：21-25.

[2] 左保河.实时洪水预报过程中的误差分布特性研究[J].华北水利水电学院学报，1997，18(2)：42-47.

[3] 刘心愿，郭生练，李 响，等.考虑水文预报误差的三峡水库防洪调度图[J].水科学进展，2011，22(6)：771-779.

[4] 董前进，傅建彬，陈森林.基于统计图形的入库流量预报误差分布规律[J]. 水电能源科学，2011，29(4)：5-7.

[5] Singh V P. The use of entropy in hydrology and water resources[J].Hydrological Processes，1997,(11)：587-626.

[6] 周惠成，李丽琴，王本德. 洪水预报误差分布的极大熵法[J].大连理工大学学报，2007，47(3)：408-413.

[7] 刁艳芳，王本德，刘 冀.基于最大熵原理方法的洪水预报误差分布研究[J].水利学报，2007，38(5)：591-595.

[8] 董前进，陈森林，王先甲.最大熵原理的洪水预报误差分布规律推求——以三峡水库为例[J].武汉大学学报(工学版)，2012，45(4)：418-422.

[9] Jaynes E T. Information theory and statistical mechanics[J].The Physical Review，1957，106(4)：620-630.

[10] J N 希德尔.工程概率设计——原理与应用[M].北京：科学出版社，1989:97-119.

[11] 唐国磊. 考虑径流预报及其不确定性的水电站水库调度研究[D]. 辽宁大连：大连理工大学,2009.

[12] 刁艳芳.双标准的水库防洪预报调度方式研究及其应用[D]. 辽宁大连：大连理工大学，2010.

[13] 叶 林，朱 远，赵永宁，等.风能资源分布特性的改进最大熵方法[J].中国电机工程学报，2014，34：6 093-6 100.