基于关联机组风险系数的发电机振荡模式辨识

林波，吕林，钟继友，吴晓蓉

(1.四川电力设计咨询有限责任公司，四川成都610041；2.四川大学电气信息学院，四川成都610065)

基于关联机组风险系数的发电机振荡模式辨识

林波1，2，吕林2，钟继友1，吴晓蓉1

(1.四川电力设计咨询有限责任公司，四川成都610041；2.四川大学电气信息学院，四川成都610065)

针对发电机功角振荡，提出基于关联机组风险系数的机组振荡模式辨识方法。首先分析Prony算法提取发电机功角振荡模式的原理，介绍了能量级理论在机组功角振荡模式辨识中的运用，结合Prony算法所抽取的振荡幅值、阻尼比和衰减因子等参数，提出了机组振荡模式评估系数——参与因子；并给出了基于该系数的主振模式具体辨识方法。最后，在IEEE39节点系统计算结果表明：所提因子能够辨识扰动下的强关联发电机组及主导振荡模式，且通过振荡模式与振荡能量级关系分析，验证了所提方法的可行性和有效性。

功角振荡；Prony算法；参与因子；主导振荡模式；强关联机组

随着我国电网大区互联的快速发展，区域间弱阻尼关系导致发电机组之间功角低频振荡频现，影响机组向系统持续供电，降低电能质量，甚至导致机组异常退出运行，严重时会危及电网安全[1－2]。作为采取针对性控制手段的主要依据，机组主导振荡模式的辨识是有着极为重要的研究意义与实际价值[3]。

主导振荡模式辨识的重点在于：发电机组动态特性和稳定性的关键信息的提取。Prony[4]算法是其中应用较为成熟的方法之一，它能从暂态仿真数据或现场实测功角数据中抽取振荡模式的幅值、频率和阻尼比等信息。但模型的具体辨识精度与算法抗噪水平、采样频率及阶数选择等相关[5－7]。如文献[5]便采用随机减量技术(RD)和Prony算法相结合的办法，利用RD技术在极值、水平穿越和零穿越三类触发条件下对噪声信号中自由衰减信号进行提取，在小扰动信号中提高了振荡模式阻尼比辨识精度；文献[6]在Prony算法基础上，提出在常规ARMA法和高阶ARMA法之间自适应切换的振荡模式辨识方案，对动态和稳态两种具备不同高斯分布特征信号进行了辨识；文献[7]则利用奇异值总体最小改进多信号Prony算法，通过小波变换降低了噪声的影响。应该说，通过提高抗噪性与模型阶次来增加辨识准确度是上述研究的主要思路。但仅通过不同振荡幅值或阻尼比的细微差别仍难以消除确定主振模式时的误差。就此，B Friedlander等人提出振荡模式能量概念[8－9]，利用辨识出的特征根定义能量级，辅助判断主振模式。然而，该方法仅局限于单个机组的振荡模式信息挖掘，缺乏系统性发电机群关联性分析，这与实际系统情况不相符合。

针对上述研究现状与问题，本文利用WAMS实时监测数据，采用Prony算法对发电机组振荡模式参数进行在线识别，并对区域振荡模式(Inter-areamodals)或局部模式(Local modals)进行决策分类；同时，兼顾振荡模式的基本参数与模式所对应的机群关联性，提出参与因子，评估振荡模式的危害程度，进而实现对振荡机群和主振模式的辨识，为进一步制定相关机组控制措施提供参考。

1 Prony算法模型

假设模型是由一系列的具有任意振幅、相位、频率和衰减因子的指数函数的线性组合，Prony算法所采用的数学模型为一组P个具有任意幅值、相位、频率与衰减因子的指数函数，其离散时间的函数形式见式(8)。

式中：N为采样点数；Ai为信号分量幅值；qi为相位；αi为衰减因子；fi表示振荡频率；Δt为采样间隔。

求取出差分方程式：

利用最小二乘估计使ai误差平方和为最小，进而可得到一组线性的矩阵方程：

式中：ε为拟合值与采样值的误差。

定义：

可得推导得Prony方程：

进一步可求解出如下特征方程的根Z：

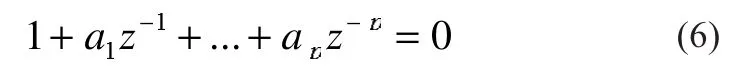
于是，数学模型(8)可简化为：

求解方程(14)并利用式(15)即可算出幅值Ai、相位qi、频率fi和衰减因子αi。

2 发电机组振荡模式的判别方法

2.1 运用能量级理论检测主导振荡模式

Prony算法为了提高模式辨识精度，降低噪声对结果的影响，n的值需大于系统特征根数nl，因此在辨识的结果中包含了抑制噪声的模式分量，准确提取对系统动态特征关联程度高的主振模式是关键。利用振荡能量级概念，通过模式能量的排序对主振模式进行辨识。

考虑到特征根共轭复数或实数形式呈现，第i个模式的能量级可以定义为：

实数模式时：

复数模式时：

基于能量级的定义，能量级较大的振荡模式为主振模式，而较小的模式可认定为非关键或不重要模式。按照振荡模式能量排序是一种简单且直接的方式，然而当信噪比(SNR)较低时，能量级误差较大。

2.2 参与因子

在小干扰分析中，通过定义参与系数——“机电回路比”用于主导振荡模式的确定[10]。

参照此定义，在Prony进行振荡模式评估时，衰减系数与阻尼比共同表征了振荡的衰减性质，是状态变量波动程度的物理量，体现了活动性。定义右特征向量的对应参数：

每一个振荡模式的幅值在该状态变量总幅值中占比，可见是状态参量对该振荡模式的参与程度。与左特征向量类比：

因此，定义基于Prony的参与因子：

考虑到参与因子评估的是该模式对整个系统的影响，故需修正参与因子。首先，计及该模式所关联到的所有机组，并引入归一化权重系数：

式中：pij表示第i个机组第j个振荡模式的参与系数，pmodel为pij集合。

则修正后的参与因子如下：

式中：ξij为阻尼比；αij为振荡衰减系数；Aij为该模式幅值。

由此得出，参与因子为Pk具体物理含义为度量振荡模式与关联机群状态变量相互参与程度。该数值越大，则此振荡模式所影响的机组越多，对发电机的稳定运行影响越大，其振荡风险也越大；反之则小。

2.3 主导振荡模式的确定

系统主导区间振荡模式的识别步骤如下：

(1)若频率在[0.1，0.8]Hz范围内，确认为区域间振荡形式；

(2)按阻尼比值大小归类振荡模式属性：若阻尼比ξ>0.15，就认为该振荡模式具有足够的阻尼，不再查找强相关机组；若0.05<ξ<0.15，说明该振荡模式没有足够的阻尼，需要考虑；若0<ξ<0.05，说明该振荡模式阻尼不足且比较严重，需要详细考虑；若ξ<0.0，说明该模式是增幅振荡模式；

(3)依据参与因子对振荡模式风险进行排序；

(4)经过上述对振荡频率、阻尼比等一系列的筛选，并通过本文提出的参与因子排序，会找到发电机组功角振荡的主导振荡模式。

3 算例分析

仿真工具：电力系统分析软件包PSD-BPA。10台机组均采用快速励磁，励磁系统放大系数为Ka=200；励磁系统时间常数Tr均取0，31号机Ta取0.05 s，30、32、33取0.06 s，其余均取0.02 s；以39号机为参考机。图1为IEEE10 39节点系统。

图1 IEEE10 39节点系统

便于比较，用PSD-BPA的小干扰稳定计算QR法模块，在给定运行方式下求解系统线性化微分方程组状态矩阵的全部特征根，按机电回路相关比从大到小排列前8位的结果如表1所示。

容易看出，表1中多个模式间的阻尼比及回路相关比差异小，对主振模式的确定存在一定困难；同时由于模式的非线性相关性，线性化方法不可避免带来误差，辨识的主导振荡模式存在不同程度误差。

通过本文所提方法进行机组振荡模式的辨识。假定故障为31号母线侧发生三相瞬时短路，切除时间tcl=0.16 s。在该大扰动条件下，系统中发电机功角曲线如图2所示。

按本文方法计算相关数据如表2所示。

可见不同振荡频率下的阻尼比系数差异较小。但是，参与因子却有着很清晰地辨识度。如通过本文方法，频率0.59Hz的模式，其振荡作用贡献因子为55.602 3，与其他振荡频率有着明显差异，且强关联机组包括了测试系统中全部机组。在所有机组功角曲线的Prony检测结果中均存在频率与区间模式0.59 Hz非常接近的低频振荡模式，这说明该模式为主导低频振荡模式。其次，超低频0.11 Hz振荡模式下的贡献因子30.591 3，远高于其他振荡模式，也是该测试系统的主要振荡模式之一。而系统其它特征值所对应的低频振荡频率并没有出现在所有机组功角曲线中，即其它低频振荡模式与部分机组不存在强关联关系。因此，通过参与因子可以辨识出主导低频振荡模式。

图2 tcl=0.16 s时系统功角曲线

Bus34参与了参与因子排名前六中所有振荡模式的振荡，是系统机群中受扰最严重的机组。因此有必要对其进一步分析。将Bus34主要振荡模态进行分解，结果如图3所示。

图3中可见，故障切除5 s后大部分模态的振荡已经被系统阻尼平抑。但0.59 Hz及0.11 Hz两个模式仍然具有较大幅值的振荡。

且7.5 s时刻0.11 Hz的振荡幅值首次超过0.59 Hz的振荡幅值，并且0.11 Hz的超低频振荡在整个振荡过程中衰减缓慢，与系统中所有机组成强关联关系，该模式的振荡风险显著。而表2结果中，参与因子对该振荡模式表现出了较强的辨识能力，而通过阻尼比无法做到，因此再次验证本文方法的有效性。

图3 Bus34主要振荡模式模态分解曲线

为了进一步说明本文方法的有效性，通过文献[8-9]所提出的振荡能量级方法在本文所测试扰动下得出的系统能量级图谱，如图4所示。

图4 系统振荡模式能量级

清楚看到，能量级方法对0.59 Hz与0.11 Hz两个主振模式的识别与本文方法得出结果是一致的，对其余模式的风险程度评估区分不明显。在Bus36中0.23 Hz的振荡模式能量级达3 651.64，超过了0.11Hz模式的3 643.99。但是0.23 Hz的阻尼比为0.622 5，因此振荡能够迅速平抑，其影响机组以及振荡时间均远小于0.11 Hz的超低频模式。因此能量级尚不能完全评估振荡风险，只能作为辅助检验方法，本文所提方法一定程度上克服了能量级方法的弊端。

4 结论

针对发电机组间功角低频振荡，本文提出了一种主振模式辨识方法：参与因子法。研究结果表明：

(1)基于Prony方法，综合考虑低频振荡模式振幅初值、衰减因子、阻尼比对动态电力系统的影响，提出依据强关联机组参与因子辨识机组主导低频振荡模式的方法，能避免仅根据各振荡模式幅值大小或阻尼比辨识主导低频振荡模式可能出现的误差，应用本文所提出参与因子能清晰地辨识出主导低频振荡模式；

(2)本文所提出辨识主振模式的方法只需获取仿真或实际发电机组功角轨迹而无需详细系统结构，为实际电力系统区间振荡风险评估，主导低频振荡模式的辨识提供了有效途径；

(3)对IEEE 10机39节点系统进行研究，发现并不是所有模式都在振荡曲线中体现出来，弱阻尼情况下0.80 Hz以下的区间振荡模式影响机组范围较广，振荡平抑困难，振荡风险较大。

[1]朱方，赵红光，刘增煌．大区电网互联对电力系统动态稳定性的影响[J]．中国电机工程学报，2007，27(l)：l-7．

[2]贺仁睦，韩志勇，周密，等．互联电力系统未知机理低频振荡分析[J]．华北电力大学学报：自然科学版，2009，36(l)：l-5．

[3]倪以信，陈寿孙，张宝霖．动态电力系统的理论和分析[M]．北京，清华大学出版社，2002：121-184．

[4]王家林，夏立，吴正国．采用改进Prony算法的电力系统故障暂态信号分析[J]．电力自动化设备，2012，32(7)：89-93．

[5]吴超，曹广忠．基于随机减量技术和Prony方法的低频振荡类噪声辨识[J].电力系统自动化，2013，37(8)：53-58．

[6]徐玉韬，卢继平，陈刚，等．稳态和动态混合信号的在线低频振荡模式辨识方法[J]．电力系统自动化，2012，36(2)：31-35．

[7]马燕峰，赵书强，刘森，等．基于改进多信号Prony算法的低频振荡在线辨识[J]．电网技术，2007，31(15)：44-49．

[8]PATEL V S，BHIL SK，KAZIFS，etal．Energy-sorted prony analysis for identification of dom inant low frequency oscillations[C]// Australian ControlConference，Perth：ACC2013，2013：85-90．

[9]ZHOU N，PIERRE JW，DANIEL．A stepw ise regression method for estimating dom inant electromechanicalmodes[J]．IEEE Transactionson Power Systems，2012，21(2)：1051-1059．

[10]闫常友，周孝信，田芳，等．电力系统在线小干扰主导特征模式识别及强相关机组选择方法[J].电网技术，2009，33(13)：42-47．

Identification of oscillationmodebased on risk factorof relevant generator

LIN Bo1，2，LV Lin2，ZHONG Ji-you1，WU Xiao-rong1
(1.Sichuan Electric PowerDesign&Consulting Co.，Ltd.，Chengdu Sichuan 610041，Chiina; 2.School ofElectrical Engineering and Information，Sichuan University，Chengdu Sichuan 610065，China)

A novel identification method for critical oscillation mode was presented by making use of risk factor of relevant generator.Prony algorithm was utilized to obtain oscillation mode of rotor angle.The energy class was introduced to indentify critical oscillation mode.The participation factor，concerning risk of oscillation relevant generators，was raised bymeans of synthesizing parameters like am plitude，dam ping ratio and attenuation obtained by Prony algorithm.The specified procedures of identifying criticaloscillationmode were proposed based on the risk factor.The simulation results of IEEE 10-machine 39-bus system show that the proposed factor is able to identify criticaloscillationmode and assess oscillation risk of the strongly relevantgenerators.Com paring the obtained result w ith that from energy class ofoscillationmodes，itverifies the feasibility and effectiveness of the proposedmethod.

rotor angle oscillation;Prony algorithm;participation factor;critical oscillation mode;strongly relevant generator sets

TM 31

A

1002-087 X(2016)07-1479-04

2015-12-05

国家自然科学基金项目(51261130472)；英国Alstom公司国际科研合作项目(11H0207)；国家电网科技项目(5441YD120008)

林波(1988—)，男，四川省人，硕士生，主要研究方向为电机电器控制，电力系统安全稳定分析。