(2+1)维非线性薛定谔方程的怪波解

程丽　(金华职业技术学院师范学院，浙江 金华 321017)

张翼　(浙江师范大学数理信息学院，浙江 金华 321004)



(2+1)维非线性薛定谔方程的怪波解

程丽(金华职业技术学院师范学院，浙江 金华 321017)

张翼(浙江师范大学数理信息学院，浙江 金华 321004)

[摘要]应用Hirota双线性算子方法得到(2+1)维非线性薛定谔方程的周期解和其极限解，利用sato算子理论把(1+1)维非线性薛定谔方程的Grammian解转化为(2+1)维非线性薛定谔方程非奇异的有理解，从而得到(2+1)维非线性薛定谔方程的一阶和高阶怪波解。研究结果说明了高维的非线性薛定谔方程具有有理分式的怪波解, 这些方法同样适用于其他的高维薛定谔型方程，如Mel’nikov方程、Fokas 系统等。

[关键词](2+1)维非线性薛定谔方程； Hirota双线性方法； 周期解； 怪波解

怪波最初是描述海洋上出现的一种奇怪的水波,它以其出现的突然性和异常陡峭的高水波得名。怪波发生之前没有任何预示, 海洋中突然出现具有很深的沟或出现一些连续的高波, 其破坏力极大, 造成很多航海灾难。怪波是一种新的非线性现象，与孤立子很类似,都是一种特殊解, 不同的是它同调制不稳定性能够很好的结合起来。近些年许多学者对怪波进行了大量的研究：Akhmediev教授小组对 (1+1)维的非线性薛定谔方程(NLS)的怪波进行了很全面的分析[1，2]，指出怪波是“Ma解”(MS)或“ Akhmediev呼吸子”(Abs)的极限情形，实际上是一种非奇异的有理解；Xu 、He 以及Wang 、Porsezian与He利用Darboux变换得到许多(1+1)维高阶薛定谔型方程的怪波解[3，4]。但现有的文献对高维薛定谔方程的怪波解研究甚少。 直到最近，Yasuhiro Ohta 教授和杨建科教授利用Hirota双线性方法得到(2+1)维DS Ⅰ和 DS Ⅱ方程的Grammian解，再利用sato算子理论将其转化为非奇异的有理解，从而得到高维的薛定谔型方程也具有有理分式的怪波解[5，6]。 这使得对高维的薛定谔型方程怪波解的寻求成为非常有意义的事。

考虑(2+1)维非线性薛定谔方程：

iψt=ψxy+Vψ

(1(a))

Vx=2∂y|ψ|2

(1(b))

当∂x=∂y时,方程(1)退化为众所周知的(1+1)维NLS方程：

iut=uxx+2|u|2u

当∂t=0,方程(1)则退化为复化的Sine-Gordon方程。

文献[7]指出该方程是具有Painlevé性质并且进行了奇异结构分析；文献[8]利用任意函数得到单孤子解和双孤子解；文献[9]利用Hirota双线性算子方法，给出了同宿轨道解及其所表示的同宿轨道。把式(1(b))两边关于x积分并代入式(1(a)),则得到：

(2)

方程(2)即文献[10]所提到的(2+1)维非线性薛定谔方程。在此基础上, 笔者对方程(1)也就是方程(2)的呼吸子即周期解以及怪波解等进行了探讨。

1周期解

利用变换：

(3)

将方程(1)化为双线性形式：

(iDt-DxDy)g·f=0

(4(a))

(4(b))

其中， Dx,Dy,Dt是Hirota算子；g*是g的共轭, α是积分常数。

以往文献在研究方程(1)时都是令α=0，为了得到怪波解,笔者将考虑α是非零实数的情形。

为了求得双线性方程(4)的解, 利用Hirota扰动方法, 将f与g按ε展开为幂级数：

f=1+εf(1)+ε2f(2)+…+εjf(j)+…

(5(a))

g=g(0)+εg(1)+ε2g(2)+…+εjg(j)+…

(5(b))

将式(5)代入式(4),并比较ε的同次幂系数得：

(6(a))

(6(b))

(6(c))

2g(0)g(0)*=α2

(7(a))

(7(b))

(7(c))

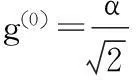
(8)

(9)

利用式(3),即可得到方程(1)的双孤子解。

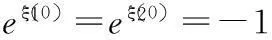
(10)

(11)

该解是含有空间x、y的周期函数，当参数α、γ、θ取特定值时，从图1中可以看出解的周期性。

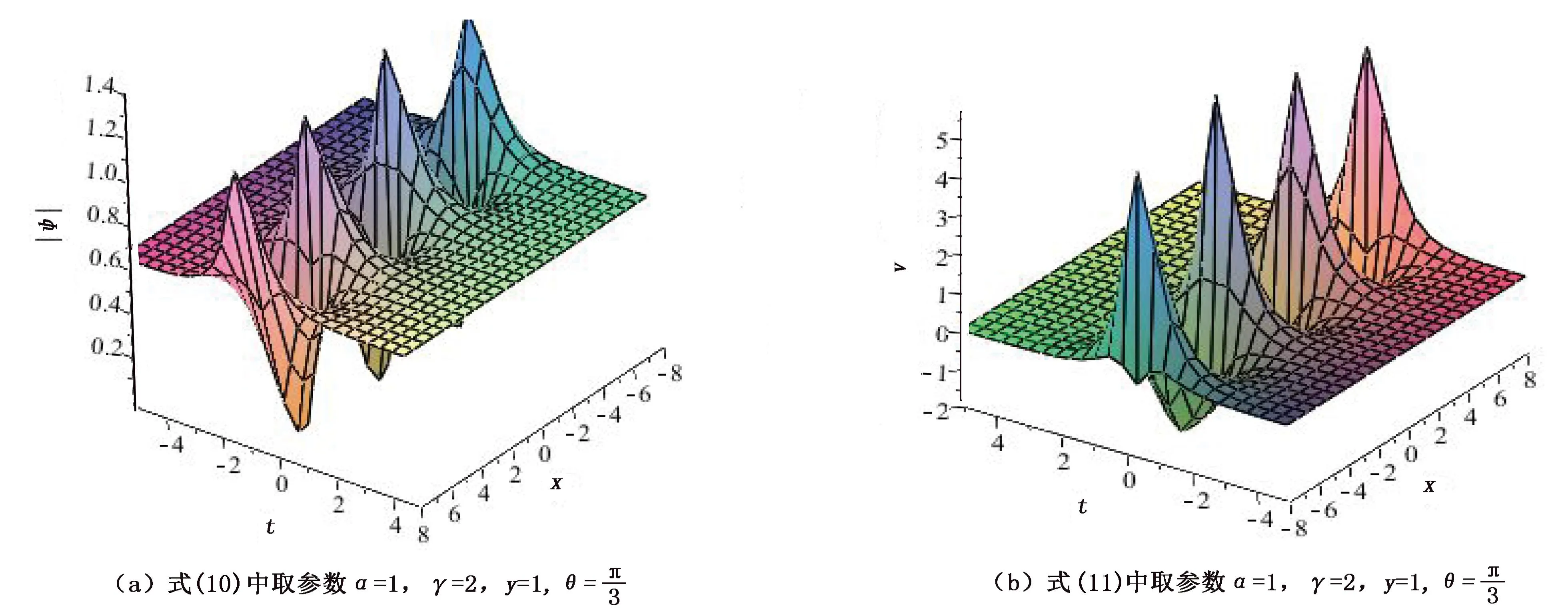
图1　Akhmediev呼吸解

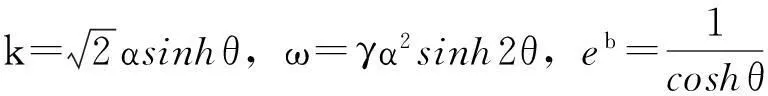
(12)

(13)

2怪波解

为了得到方程(1)的怪波解，在式(10)、式(11)中令θ→0，则有：

(14)

(15)

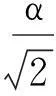
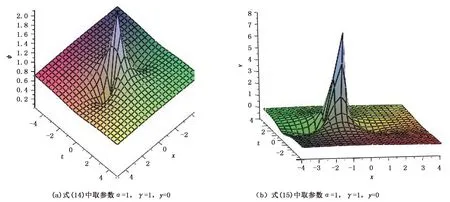
图2　一阶怪波解

文献[11]对(1+1)维NLS方程的Grammian行列式解，利用sato算子理论转化为非奇异的有理解，同样得到与文献[2]一致的一阶和二阶怪波解。

满足双线性方程：

(16)

(17)

利用引理1，通过变量代换x1=x+y,x2=-it可以得到定理1。

定理1方程(1)有非奇异的有理解：

其中：

(18)

行列式元素定义为：

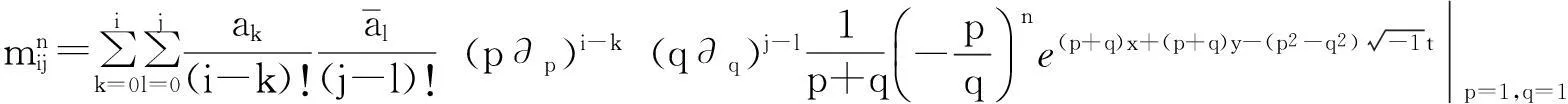
该解就是利用Hirota方法所得到的怪波解，即在式(14)和式(15)中令γ=1,α2=2。

(19)

其中：

σ1=9-72(x+y)2-48(x+y)4-864t2-3840t4-1152(x+y)2t2

+it[-180-288(x+y)2+192(x+y)4+384t2+3072t4+1536(x+y)2t2]

-288(x+y)2t2+768(x+y)2t4+192(x+y)4t2

从图3中看到，当x+y=0,t=0时,|ψ|达到最大值5。

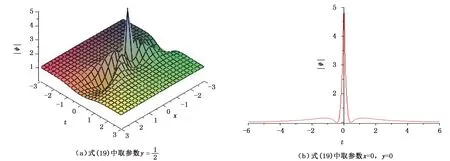
图3　二阶怪波解

3结语

应用Hirota双线性方法,给出(2+1)维非线性薛定谔方程(1)的呼吸子即周期解和其极限情形的解——一阶怪波解，推广了(1+1)维非线性薛定谔方程NLS的空间变量。此外，在(1+1)维NLS的Grammian行列式解的基础上, 利用sato算子理论得到的方程(1)的一阶和高阶怪波解，其中该方法得到的一阶怪波解包含于Hirota双线性方法给出的怪波解中，但利用定理1易获得高阶怪波解。研究结果说明了高维的非线性薛定谔方程具有有理分式的怪波解, 这些方法同样适用于其他的高维薛定谔型方程，如Mel’nikov方程、Fokas 系统等。

[参考文献]

[1]Akhmediev N, Ankiewicz A，Taki M.Waves that appear from nowhere and disappear without a trace[J].Phys Lett A, 2009(373): 675～678.

[2] Akhmediev N, Ankiewicz A，Soto-Crespo J M.Rouge wave and rational solutions of the nonlinear Schrödinger equation[J].Phys Rev E, 2009(80): 026601.

[3] Xu S W，He J S. The rogue wave and breather solution of the Gerdjikov-Ivanov equation[J].J Math Phys, 2012(53): 063507.

[4] Wang L H, Porsezian K，He J S.Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation[J].Phys Rev E, 2013(87): 053202.

[5] Ohta Y,Yang J K.Rouge waves in the Davey-Stewartson: I.Equation[J].Phys Rev E,2012 (86): 036604.

[6] Ohta Y, Yang J K.Dynamics of rouge waves in the Davey-Stewartson Ⅱ equation [J].J Phys A: Math Theor, 2013,(46): 105202.

[7] Radha R,Lakshmanan M.Singularity structure analysis and bilinear form of a (2+1)-dimensional nonlinear Schrödinger (NLS) equation[J].lnverse Problems, 1994,10:29～33.

[8] Strachan I A B.Wave solutions of a (2+1)-dimensional generalization of the nonlinear Schrödinger equation [J].lnverse Problems, 1992,8:21～27.

[9]沈守枫，张隽.(2+1)维非线性Schrödinger型方程的同宿轨道[J] .应用数学和力学,2008(29): 1254～1260.

[10] Zhang H Q , Tian B, Li L L,et al.Darboux transformation and soliton solutions for the (2+1)-dimensional nonlinear Schrödinger hierarchy with symbolic computation[J].Physica A, 2009,388: 9～20.

[11] Ohta Y,Yang J K.General high-order rouge waves and their dynamics in the nonlinear Schrödinger equation[J].Proc R Soc A, 2011,468:1716～1740.

[编辑]洪云飞

[文献标志码]A

[文章编号]1673-1409(2016)07-0035-05

[中图分类号]O175.24

[作者简介]程丽 ( 1972- )，女，硕士， 副教授，现主要从事应用数学方面的教学与研究工作；E-mail: jhchengli@126.com。

[基金项目]国家自然科学基金项目( 11371326 )。

[收稿日期]2015-11-29

[引著格式]程丽,张翼.(2+1)维非线性薛定谔方程的怪波解[J].长江大学学报(自科版)，2016,13(7)：35～39.