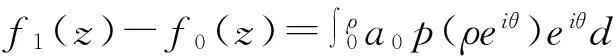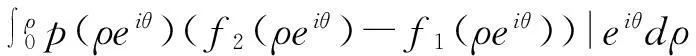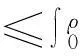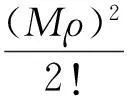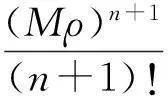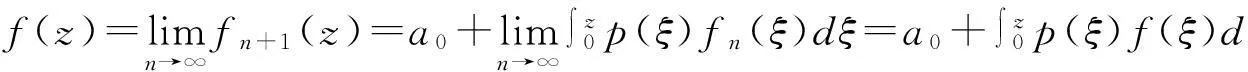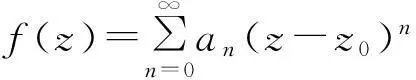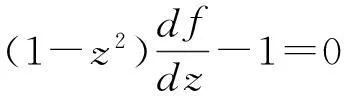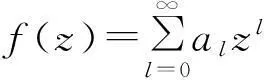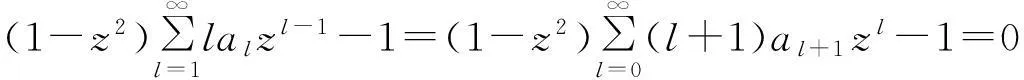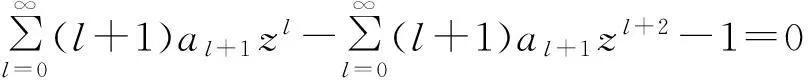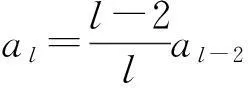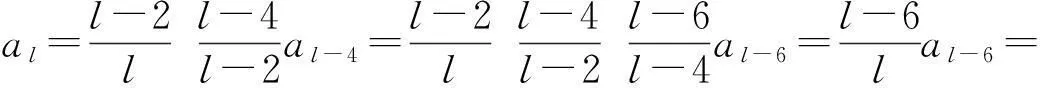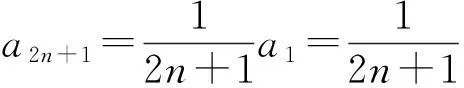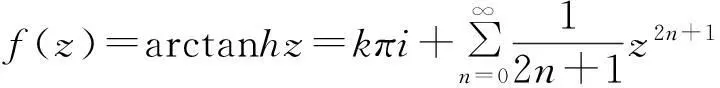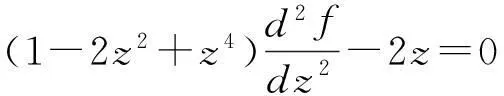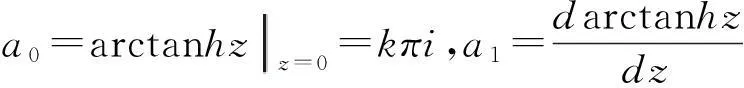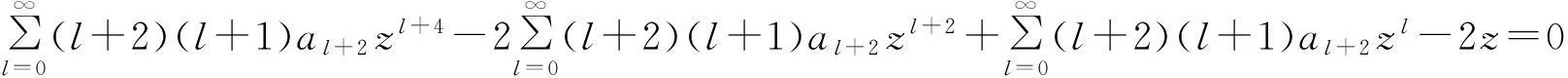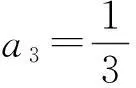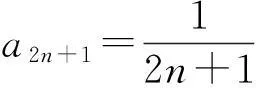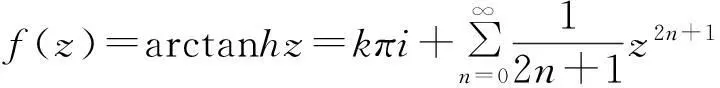解析函数泰勒展开的一种新方法

刘灯明

(湖南科技大学数学与计算科学学院，湖南湘潭 411201)



解析函数泰勒展开的一种新方法

刘灯明

(湖南科技大学数学与计算科学学院，湖南湘潭 411201)

[摘要]解析函数的泰勒展开是复变函数论中的一个重要内容，利用线性常微分方程的幂级数解，可以简洁地求得一些复杂解析函数的泰勒展式。

[关键词]解析函数；泰勒展开；常微分方程幂级数解

解析函数的泰勒展开是复变函数论课程中的一个重要知识点，内容灵活多变，学生较难掌握.要求解析函数f(z)在z=z0点的泰勒展开式，可由泰勒定理直接求解，即从已知的f(z)，求出fn(z0)，从而求出泰勒系数.但很多时候，任意阶导数的计算比较复杂，甚至无法进行.大部分情况下，需要根据泰勒展式的唯一性，利用已知的泰勒展式(如ez、sinz、cosz、ln(1+z)、(1+z)a等常见初等函数的泰勒展式)，经过一定的处理(如变量代换、部分分式、级数的乘除运算、逐项求导或求积等)之后，求得f(z)的泰勒展开[1].本文从另外一个角度，即利用线性常微分方程的幂级数解来对一些复杂解析函数的泰勒展开式进行讨论.

1利用常微分方程的级数解求泰勒展式的理论依据

定义1如果方程

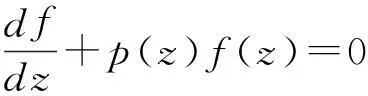
(1)

的系数p(z)在点z0及其邻域内是解析的，则点z0称为方程(1)的常点.若p(z)在点z0不解析，则称z0为方程(1)的奇点.

定义2如果方程

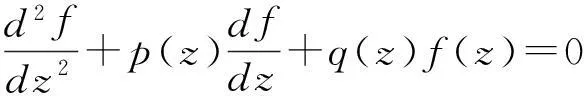
(2)

的系数p(z)和q(z)都在点z0及其邻域内是解析的，则点z0称为方程(2)的常点.若系数p(z)或q(z)在点z0不是解析的，则称点z0为方程(2)的奇点.

定理1如果p(z)在圆|z-z0|

f(z0)=a0，a0为任意常数.

(3)

且f(z)在此圆内是解析的.

证明作函数序列

(4)

n=0，1，2，….由于该函数序列中的被积函数是解析的，故(4)为解析函数序列.因此，积分值与积分路径的选取无关.不妨选取积分路径为过点z及z0的直线，且为了方便，假设z0=0.接下来，令

z=ρeiθ，0≤ρ≤R1

则有

注意到p(z)在圆|z-z0|

|f1(z)-f0(z)|≤|a0|Mρ.

进一步

重复上述步骤，由数学归纳法，可以证明

可见，上述不等式的右边为指数函数|a0|eMρ泰勒展开的普通项，因此，序列

fn+1(z)=f0(z)+(f1(z)-f0(z))+…+(fn+1(z)-fn(z)).

在|z|≤R1内一致收敛.进一步，由魏尔斯特拉斯定理，该序列的极限函数f(z)是|z|

另一方面

显然，f(z)满足方程(1)及初始条件(3).这样就证明了|z-z0|

下面再证唯一性.假设g(z)为方程(1)在初始条件(3)下的另一解析解，则容易证明：存在正数A，使得

上式两边关于n→∞取极限，得|f(z)-g(z)|≡0，即f(z)≡g(z).

由定理1，可以把f(z)在z0点的邻域|z-z0|

(5)

显然，(z-z0)0的系数a0正好和初值条件(3)一致.而(z-z0)n的系数an(n=1，2，3，…)均可由a0表出.事实上，只需将级数解(5)代入到微分方程(1)，比较两端同次幂的系数即可.

类似于定理1的讨论，则有

定理2如果p(z)、q(z)在圆|z-z0|

f(z0)=a0，f′(z0)=a1，a0和a1为任意常数.

(6)

且f(z)在此圆内是解析的.

由定理2，可以把f(z)在z0点的邻域|z-z0|

2利用常微分方程的级数解求泰勒展式

例求函数f(z)=arctanhz在z=0邻域内的泰勒展式.

解一容易验证f(z)=arctanhz满足如下一阶线性常微分方程

(7)

且z=0是方程的常点，故在z=0的邻域内应有泰勒级数形式的解.不妨设其泰勒级数解为

(8)

并知

将(8)代入方程(7)可得

即

比较等式两端同次幂的系数，得到

z0的系数：a1-1=0，即a1=1；

z1的系数：a2=0；

…………

由此可递推出

所以

解二容易验证f(z)=arctanhz满足如下二阶线性常微分方程

(9)

且z=0是方程的常点，故在z=0的邻域内f(z)可展开成形如(8)式的泰勒级数，并知

将(8)代入方程(9)可得

比较等式两端同次幂的系数，得

z0的系数：2a2=0，即a2=0；

z2的系数：12a4-4a2=0，推出a4=0；

…………

zl-1的系数(l≥4)：(l-2)(l-3)al-2-2l(l-1)al+(l+2)(l+1)al+2=0.

由此容易看出，若l=2n，则a2n=0；另一方面，若l=2n+1，则可用数学归纳法证明

所以

综上所述，我们不难发现，利用常微分方程的幂级数解来对解析函数进行泰勒展开，只需将幂级数解代入到解析函数所满足的微分方程(一阶或二阶)进行确定，然后比较系数，就可方便、快捷地得到该解析函数的泰勒展式.

[参考文献]

[1]钟玉泉.复变函数学习指导书[M].北京:高等教育出版社,2005.

[2]王高雄,周之铭,朱思铭,等.常微分方程[M].北京:高等教育出版社,2006.

[3]钟玉泉.复变函数论[M].北京:高等教育出版社,2012.

[4]吴崇试.数学物理方法[M].北京:北京出版社,2015.

A New Approach for Taylor Expansion of Analytic Function

LIU Deng-ming

(School of Mathematics and Computational Science, Hunan University of Science and Technology,Xiangtan Hunan 411201, China)

Abstract:Taylor expansion is one of the most important contents of Complex analysis. By using the series solution of the linear ordinary differential equations, Taylor expansions of some complicated analytic functions are obtained.

Key words:analytic function; Taylor expansion; series solution of the linear ordinary differential equations

[中图分类号]O173.1

[文献标识码]A

[文章编号]2095-7602(2016)04-0004-04

[作者简介]刘灯明(1984- )，男，讲师，博士，从事非线性偏微分方程研究。

[基金项目]湖南省教育厅资助科研项目“退化抛物方程的非完全爆破与多重爆破研究”(14B067)；2015年湖南科技大学教学研究与改革一般项目“信计专业《数学分析》课程的教学研究与实践”(G31515)。

[收稿日期]2016-01-22